UAB MATH-BY-MAIL CONTEST, 2004
|
|
|
- Thomas Harmon
- 5 years ago
- Views:
Transcription
1 UAB MATH-BY-MAIL CONTEST, 2004 ELIGIBILITY. Math-by-Mail competition is an individual contest run by the UAB Department of Mathematics and designed to test logical thinking and depth of understanding of mathematics by high school students. The contest is open to all high school students from participating schools. PRIZES AND CEREMONY. One first prize ($60 and trophy), onetwo second prizes ($40 and a trophy) and some third prizes ($20 and an award diploma) will be handed out (since awards/prizes to individuals are reportable annually by UAB to the IRS, cash prize-winners will have to have a valid U.S. federal tax identification number, will need to fill out W-9/W-8 form prior to receiving cash prizes, and will need to report prizes on their tax returns). All other participants will receive certificates honoring their participation. The school with the best overall performance will be awarded the UAB traveling Math trophy. Prize winners will be invited to an awards ceremony at UAB at a later announced date. Parents and teachers will also be invited. The program will feature awards presentation and refreshments. RULES AND JUDGING. Math-by-Mail contest is an individual contest. Students must solve problems on their own. All solutions must be selfcontained; no references to facts and mathematical results beyond the high school standard curriculum are permitted (nor will they be necessary). The explanations must be detailed and thorough, all answers must be explained and justified! Professors of the Department of Mathematics at UAB will judge the entries and evaluate your reasoning process and method of finding the solution. Criteria will include correctness and elegance of solutions. The decision of the judges is final. The entries will not be returned. FORMAT AND CONTACTS. The participating schools will receive problems and cover sheets before or on Monday, February 9. On Monday, February 9, the problems and cover sheets should be made available to the students. Every participant must submit a filled copy of the cover sheet; each solution must be written on a separate sheet of paper with the student name and the school name on it. The entries must be postmarked no later than Monday, February 23, and mailed to: UAB Math-by-Mail Contest c/o Dr Alexander Blokh Department of Mathematics, UAB 1300 University Blvd, CH 452 Birmingham AL For additional information you can contact us at (205) or by electronic mail at ablokh@math.uab.edu 1
2 2 UAB MATH-BY-MAIL CONTEST COVER SHEET (1) YOUR NAME (2) YOUR SCHOOL (3) YOUR GRADE (4) YOUR ADDRESS (5) YOUR PHONE NUMBER (6) YOUR ADDRESS (IF ANY)
3 UAB MATH-BY-MAIL CONTEST 2004, PROBLEMS Solve the problem(s) and write each solution on a separate sheet of paper with your name and your school s name on it. If you can (and only after you have done as much as you could solving problems), try to see if you can solve more general problems using your methods. Some third prizes will be awarded for particularly good solutions of individual problems, so you can win a third prize for an excellent job in just one problem! Complete your cover sheet (see your teacher to get one) and include it with your submission. Submit your entries (postmarked by February 23, 2004) to: UAB Math-by-Mail Contest c/o Dr Alexander Blokh Department of Mathematics, UAB 1300 University Blvd, CH 452 Birmingham AL PROBLEMS PROBLEM 1. Find all two-digit numbers x with digits a, b such that x 2 = (a + b) 3. PROBLEM 2. There are n points given on the plane. For any three points A, B, C from this collection the angle ABC is formed. Then among all these angles the least one is chosen. What is the greatest possible value of such an angle (as a function of n)? Note: if three points belong to a line then some angles they form are equal to 0. PROBLEM 3. A square n n table is filled with real numbers. For any given row and column the sum of their 2n 1 numbers taken together is greater than or equal to a real number X. What is the minimal possible value of the sum of all numbers in the table? PROBLEM 4. A closed broken line consists of 203 straight links. It is known that no 2 links are contained in the same line. What is the greatest number of self-intersections such a broken line may have? PROBLEM 5. A 4 4 table is filled with plus or minus signs. An admissible action is the change of all signs to the opposite in a row or in a column. The minimal number of minuses which can be obtained from a given table after a finite sequence of admissible actions is called the characteristic of the table. List all possible characteristics of various 4 4 tables (giving examples of tables generating them) and prove that no other characteristics are possible. 3
4 4 UAB MATH-BY-MAIL CONTEST 2003, PROBLEMS AND THEIR SOLUTIONS PROBLEM 1. Find all two-digit numbers x with digits a, b such that x 2 = (a + b) 3. Solution: Let the 2-digit number be 10a + b with a 0. We need to solve an equation (10a + b) 2 = (a + b) 3 = N. Thus, any prime number in the factorization of N is involved in the power which is divisible by both 2 and 3, hence it is divisible by 6. Hence N is in fact the sixth power of some number k. This implies that a + b is the square of some number. On the other hand a + b 18. So, a + b may be equal 1, 4, 9, 16 with the corresponding values of 10a + b being 1, 4, 27, 64. Now, 1 and 4 are not 2-digit numbers while a simple verification shows that 64 is not the answer. On the other hand, 10a + b = 27 satisfies the conditions. So, the answer is 27. PROBLEM 2. There are n points given on the plane. All possible angles with the vertices at these points are made and then the least one is chosen. What is the greatest possible value of such angle? Note: if three points belong to a line then some angles they form are equal to 0. Solution: First of all, observe that if there are 3 points which belong to one line, then there are angles equal to 0 formed by them. If however there are no such 3 points then no angle formed by any 3 points equals 0. Hence we may from now on consider only such sets of n points that no 3 point belong to the same straight line. Now, denote a collection of n points by A. Then we can always choose the so called convex hull of A, i.e. the smallest convex set containing A. Indeed, for any finite ordered collection of points from A we can connect them in this order with the agreement that the last point must be connected to the first one. Some of these broken lines will be actually convex polygons. Of course, not all of such polygons contain all the other points. However, if this is not the case, then there must be a point from A which is outside this polygon. It is easy to see that then we can connect this point and some vertices of the polygon and thus create a new convex polygon with vertices at some of our points which will contain the previous polygon and will not coincide with it. This process cannot last forever, so it will stop with some convex polygon P whose vertices belong to A will contain all points of A. If there is another convex polygon P with the same properties then it will have to contain P while P will have to contain P so P = P and the polygon P (called convex hull of A) is well-defined. Now, suppose that P is a k-gon while there are n points overall. It is known that the sum of angles of P then is π(k 2) and hence the least of the angles
5 5 of P is π(1 2 ). Suppose that the corresponding vertex of P is a point x. k The point x is already connected with two points of A by the sides of P. We can connect x with remaining points of A by straight lines and consider all lines created like this. Clearly there will be n 1 such lines. Moreover we can number them moving say in the counterclockwise direction from side of P to the other side of P where both sides come out of x. It is clear that π then the least angle of all these angles is going to be at most n 2 (1 2 k ). Observe that the greater k is the greater this quotient is, so the greatest its π value is n 2 (1 2 n ) = π/n. This implies that the greatest possible smallest angle of all the angles formed by the points from a collection of n points is at most π/n. To observe that this level can be achieved consider a right n-gon. Then all its angles are π(n 2) and if then we connect all its vertices then the minimal angles n formed by them are all equal π n. So the answer indeed is π n. PROBLEM 3. A square n n table is filled with numbers. For any given a row and a column it is known, that the sum of their numbers is no less than a. What is the minimal possible value of the sum of all numbers in the table? Solution: Denote the sum of all entries in the table by N. Choose the row in which the sum of the entries is minimal and denote it by B; denote the sum of all entries of B by b. For the sake of definiteness assume that B is the bottom row of the table. For any column and B the sum of all their entries is at least a. Each such sum can be viewed as the sum of the entries of B and entries of the corresponding column without the bottom entry. Therefore the sum s of numbers for all such pairs (B and a column) is at least na. On the other hand, in this sum s the row B is repeated n times while otherwise we sum up all columns without their bottom entries. Hence in fact s = N + (n 1)b na. By the choice of B we have that b N n, so N + (n 1) N n s na and hence N a n2. It remains to give an 2n 1 example of how the table can be filled out so that N = a, and this 2n 1 a can be done by simply putting in each place of the table. 2n 1 n2 So, the answer is N = a 2n 1 n2
6 6 PROBLEM 4. A closed broken line consists of 203 links. It is known that no 2 links are contain in the same line. What is the greatest number of self-intersections such broken line may have? Solution: Observe that a link in the broken line can intersect with no more than 200 other links at points which are not its endpoints. Thus, the overall number of intersections counted for each link giving rise to it is at most 40600, and so the overall number of self-intersections is at most (we need to divide by 2 because each self intersection is counted twice). To get this number of self-intersections, take the right 203-gon constructed inside a unit circle and connect its vertices in the order described below. Number the vertices from 1 through 203 counterclockwise. Then take each vertex A, count 101 vertices from it and get the next vertex B. Connect A with B and do this for each vertex A. For example, 1 is the connected with 102, 102 is connected with 203, 203 is connected with 101 and so on. It is easy to see that then we do get a closed broken line with 203 links. Each link in this line intersects all other links except for the ones adjacent to it because by the construction all other links begin and end on the distinct sides of the chosen link. It remains to show that no 3 links intersect at one point. Indeed, each link connects two points on the circle such that the arc between these two points is 2π 101. Let us show that given an angle 203 α < π, 3 distinct chords in the circle which are bounded by the arcs of the radian measure α cannot intersect at one point. Indeed, let us associate to any chord the segment connecting the center of the circle and the midpoint of the chord and call this segment a characteristic segment of the chord. Clearly, the characteristic segment of a chord is perpendicular to it. The fact that our chords correspond to the arcs of the same radian measure means that the length of their characteristic segments is the same and equals, say, x < 1 (recall that the radius of the circle is 1). Fix a chord A and see at what points other chords from our collection of chords can intersect A. To do so we measure the distance d between the midpoint of A and the point of intersection. Then if the angle between the characteristic segment of A and that of some other chord is β then we see that the distance d is x tan(β/2). Moreover, depending on the side from which the other chord is located with respect to A the point of intersection may be on either side of the midpoint of A. This implies the desired and completes the solution. So, the answer is PROBLEM 5. A 4 4 table is filled with pluses or minuses. An admissible action is the change of all signs to the opposite in a row or in a column. The minimal number of minuses which can be obtained from a given table after a few admissible actions is called the characteristic of the table. List
7 all possible characteristics of various 4 4 tables (giving examples of tables generating them) and prove that no other characteristics are possible. 7 Solution: Any table with pluses and minuses which cannot be changed (in one or more steps) so that the overall number of minuses decreases is called minimal. Then any such minimal table cannot be changed to decrease the number of minuses in one step either, hence the number of minuses in any row or column is no more than 2 and the overall number of minuses in such a table is no more than 8. Let T be a table. Denote by c(t ) its characteristic. Suppose that M is a minimal table and show that c(m) 4. Consider a few cases assuming by way of contradiction that c(m) > 4. First of all suppose that there are 4 cells in M which contain minuses and form a horizontal-vertical rectangle (in other words, these cells are places of intersection of two rows with two columns). Without loss of generality we may assume that these cells are actually the corner-cells of the table. Then one more minus must stand somewhere in the table. It cannot stand in a boundary cell of the table since otherwise there will be three minuses in one row or column. However if it stands inside a small 2-subtable in the middle of the given table then we can change signs in the top and the bottom rows and get 3 minuses in the same column, i.e. the column of the 5-th minus. Clearly this contradicts the minimality of M. Now, since there are at least 5 minuses in M then there exists a row with 2 minuses. Again without loss of generality we may assume that they stand in the bottom corners. If the 2nd or the 3rd column has 2 minuses then we can change signs in the bottom row and get 3 signs in the same column, a contradiction. Hence either 1st or 4th column must contain a minus. Again without loss of generality we may assume that the left top corner contains minus. Consider the possible locations of the guaranteed remaining 2 minuses. Observe that they cannot stand in the 1st column or in the bottom row; the right top corner cannot contain minus either. Suppose that there is one more minus in the top row; for the sake of definiteness assume that it stands in the 2nd column. Then the 5th minus must stand in the 3rd column or in the 4th column. If it stands in the 3rd column we can change signs in the top and bottom rows and get 3 minuses in the 3rd column; if it stands in the 4th column we can change signs in the top row and get 3 minuses in the 4th column. Either way we get a contradiction, so there are no more minuses in the top row. By the symmetry there are no minuses in the 4th column. Hence the 2 minuses must stand in the 2 2-subtable in the center. Changing signs in the top and bottom rows we get a column in the middle with 3 minuses, a contradiction. So, M cannot
8 8 contain more than 4 minuses. Let us show now that c(m) may be equal to 0, 1, 2, 3, 4. Indeed, suppose the only minuses in M are k minuses standing on the main diagonal of the table and show that then c(m) = k. Observe, that then to begin with there are k columns with the following property: no two columns from this collection coincide or are reflections (in the obvious sense) of each other. Let us prove that then the same property will hold for the same columns after several changes of signs. Indeed, if 2 columns are not equal/reflections of each other, then neither are they after one change regardless of whether the change is a column change or a row change. Thus, after any number of changes there will be k columns which are neither pairwise equal nor pairwise reflections of each other. This implies that even if one of them has no minuses after several changes then al others must have at least one minus, and so there are at least k 1 minuses in any table obtained from M. Since the parity of the number of minuses is obviously kept after all the changes this implies that in fact the number of minuses in any table obtained from M is at least k as desired. Another way to construct examples of tables M such that c(m) = 0, 1, 2, 4 was suggested by Dr N. Chernov. Observe that if 4 small squares in the table stand at the intersections of two rows and two columns (in other words, form a rectangle with horizontal and vertical sides) then the product of their entries does not change after any number of admissible actions (because any such action replaces two of the entries by their opposites). So, we can proceed as follows: a) divide the table into 4 subtables each of which is formed by 4 small squares in the table located in the upper left, upper right, lower left and lower right part of the table). Now, choose, say, 3 of those subtables and out in them exactly one minus while filling out the rest of the entire table with pluses. As we saw, admissible actions do not lower the number of minuses in any of those 4 subtables into which the table is divided. Hence, for this table M we have c(m) = 3. Similarly we can suggest tables M with c(m) equal to 0, 1, 2, 4. So, the answer is that c(m) can be 0, 1, 2, 3, 4 only.
9 9 UAB MATH-BY-MAIL 2004 AWARD CEREMONY 1. Tea 2. Speech: Dr Mayer (overall 83 students participated in the contest!). 3. Handing out awards. a) Schools Honorable Mentions: ASFA, 1 participant Auburn High, 2 participants Buckhorn High, 1 participant Grissom High, 3 participants Hoover High School, 21 participants Minor High, 1 participant Vestavia High, 54 participants b) Traveling Trophy: Vestavia High School c) Individual Trophies: Honorable Mentions: Ellie Barr, Vestavia Mingwei Gu, Hoover Misha Kotov, Vestavia Mark Mennemeyer, Vestavia Vedran Oruc, Vestavia Christopher Turndrop, Vestavia Third prize: David Harris, Vestavia Second prize: Xun Liu, Auburn First Prize: Fan Young, ASFA
Unit 7. Math Problem 1. This segment will go through the endpoint of the original line segment, perpendicular to the line segment.
 Math 1007 Unit 7 1 Construct a square with sides equal to r. 1: Extend the segment and draw a circle centered at one of the endpoints of the segment 2: Draw two larger congruent circles centered where
Math 1007 Unit 7 1 Construct a square with sides equal to r. 1: Extend the segment and draw a circle centered at one of the endpoints of the segment 2: Draw two larger congruent circles centered where
Sum Fun Tournament Meeting (Multiple Topics)
 Sum Fun Sum Fun Tournament Meeting (Multiple Topics) Sum Fun Topic There are a wide range of topics and difficulty levels covered during this meeting. Materials Needed The first four items listed below
Sum Fun Sum Fun Tournament Meeting (Multiple Topics) Sum Fun Topic There are a wide range of topics and difficulty levels covered during this meeting. Materials Needed The first four items listed below
2019 State Competition Sprint Round Problems 1 30
 1 19 State Competition Sprint Round Problems 1 3 HONOR PLEDGE I pledge to uphold the highest principles of honesty and integrity as a Mathlete. I will neither give nor accept unauthorized assistance of
1 19 State Competition Sprint Round Problems 1 3 HONOR PLEDGE I pledge to uphold the highest principles of honesty and integrity as a Mathlete. I will neither give nor accept unauthorized assistance of
2017 AMC 12B. 2. Real numbers,, and satisfy the inequalities,, and. Which of the following numbers is necessarily positive?
 2017 AMC 12B 1. Kymbrea's comic book collection currently has 30 comic books in it, and she is adding to her collection at the rate of 2 comic books per month. LaShawn's comic book collection currently
2017 AMC 12B 1. Kymbrea's comic book collection currently has 30 comic books in it, and she is adding to her collection at the rate of 2 comic books per month. LaShawn's comic book collection currently
Circle Terms.notebook March 27, 2017
 10.01+.notebook March 27, 2017 Welcome back! It's so good to see you! New seats today. Check the seating chart on the front chair. Do not move the desks as they are supposed to be in pods. In your groups...
10.01+.notebook March 27, 2017 Welcome back! It's so good to see you! New seats today. Check the seating chart on the front chair. Do not move the desks as they are supposed to be in pods. In your groups...
2015 π Math Contest. Individual Round SOLUTIONS
 015 π Math Contest Individual Round SOLUTIONS 1. (Ali Gurel) 7 3 =? Answer (1): 7 3 = 7 6 = 1.. (Alicia Weng) In the diagram below, a rectangle is split into two halves by a horizontal line segment. Then
015 π Math Contest Individual Round SOLUTIONS 1. (Ali Gurel) 7 3 =? Answer (1): 7 3 = 7 6 = 1.. (Alicia Weng) In the diagram below, a rectangle is split into two halves by a horizontal line segment. Then
Areas of Parallelograms and Triangles 7-1
 Areas of Parallelograms and Triangles 7-1 Parallelogram A parallelogram is a quadrilateral where the opposite sides are congruent and parallel. A rectangle is a type of parallelogram, but we often see
Areas of Parallelograms and Triangles 7-1 Parallelogram A parallelogram is a quadrilateral where the opposite sides are congruent and parallel. A rectangle is a type of parallelogram, but we often see
2018 Chapter Competition Countdown Round Problems 1 80
 2018 Chapter Competition Countdown Round Problems 1 80 This booklet contains problems to be used in the Countdown Round. 2018 MATHCOUNTS National Competition Sponsor National Sponsors Raytheon Company
2018 Chapter Competition Countdown Round Problems 1 80 This booklet contains problems to be used in the Countdown Round. 2018 MATHCOUNTS National Competition Sponsor National Sponsors Raytheon Company
Besides the reported poor performance of the candidates there were a number of mistakes observed on the assessment tool itself outlined as follows:
 MATHEMATICS (309/1) REPORT The 2013 Mathematics (309/1) paper was of average standard. The paper covered a wide range of the syllabus. It was neither gender bias nor culture bias. It did not have language
MATHEMATICS (309/1) REPORT The 2013 Mathematics (309/1) paper was of average standard. The paper covered a wide range of the syllabus. It was neither gender bias nor culture bias. It did not have language
Furman University Wylie Mathematics Tournament Ciphering Competition. March 10, 2007
 Furman University Wylie Mathematics Tournament Ciphering Competition March 10, 2007 House Rules 1. All answers are integers(!) 2. All answers must be written in standard form. For example, 8 not 2 3, and
Furman University Wylie Mathematics Tournament Ciphering Competition March 10, 2007 House Rules 1. All answers are integers(!) 2. All answers must be written in standard form. For example, 8 not 2 3, and
A B
 Bicentennial Olympiad Qualifying Round PROBLEM ONE The figure at the right is a magic square with missing entries. When complete, the sum of the four entries in each column, each row, and each diagonal
Bicentennial Olympiad Qualifying Round PROBLEM ONE The figure at the right is a magic square with missing entries. When complete, the sum of the four entries in each column, each row, and each diagonal
Chapter 10. Right Triangles
 Chapter 10 Right Triangles If we looked at enough right triangles and experimented a little, we might eventually begin to notice some relationships developing. For instance, if I were to construct squares
Chapter 10 Right Triangles If we looked at enough right triangles and experimented a little, we might eventually begin to notice some relationships developing. For instance, if I were to construct squares
21st AMC (A) 1 (B) 2 (C) 3 (D) 4 (E) 5
 21st AMC 8 2005 2 1. Connie multiplies a number by 2 and gets 60 as her answer. However, she should have divided the number by 2 to get the correct answer. What is the correct answer? (A) 7.5 (B) 15 (C)
21st AMC 8 2005 2 1. Connie multiplies a number by 2 and gets 60 as her answer. However, she should have divided the number by 2 to get the correct answer. What is the correct answer? (A) 7.5 (B) 15 (C)
First Name: Last Name: Student scores will be sent to the address you provide above.
 Mathworks Math Contest For Middle School Students October 14, 2014 PROCTORING TEACHER COVER SHEET! Please complete the following fields and return this cover sheet with all student exams! Only one Proctoring
Mathworks Math Contest For Middle School Students October 14, 2014 PROCTORING TEACHER COVER SHEET! Please complete the following fields and return this cover sheet with all student exams! Only one Proctoring
2011 Canadian Intermediate Mathematics Contest
 The CENTRE for EDUCATION in MATHEMATICS and COMPUTING www.cemc.uwaterloo.ca 011 Canadian Intermediate Mathematics Contest Tuesday, November, 011 (in North America and South America) Wednesday, November
The CENTRE for EDUCATION in MATHEMATICS and COMPUTING www.cemc.uwaterloo.ca 011 Canadian Intermediate Mathematics Contest Tuesday, November, 011 (in North America and South America) Wednesday, November
Mad Hatter 6-8. Math Field Day Mad Hatter 6-8. Part I
 Mad Hatter 6-8 Math Field Day 2012 Mad Hatter 6-8 CSU Fresno http://www.csufresno.edu/math 21 April 2012 The Mad Hatter Marathon is a competition in rapid computation and problem solving. You will find
Mad Hatter 6-8 Math Field Day 2012 Mad Hatter 6-8 CSU Fresno http://www.csufresno.edu/math 21 April 2012 The Mad Hatter Marathon is a competition in rapid computation and problem solving. You will find
Grade 7 & 8 Math Circles Pair-O -Dice: The Game April 2/3, 2013
 Faculty of Mathematics Waterloo, Ontario N2L 3G1 Instructions Set Up Grade 7 & 8 Math Circles Pair-O -Dice: The Game April 2/3, 2013 Get into a group of 3 to 5 players. Each group needs 2 different dice
Faculty of Mathematics Waterloo, Ontario N2L 3G1 Instructions Set Up Grade 7 & 8 Math Circles Pair-O -Dice: The Game April 2/3, 2013 Get into a group of 3 to 5 players. Each group needs 2 different dice
A 28-inch ribbon was cut into four equal lengths. How long was each piece of ribbon?
 Name Score Benchmark Test 1 Math Course 1 For use after Lesson 0 1. (5) A -inch ribbon was cut into four equal lengths. How long was each piece of ribbon? A. 7 inches B. 7 1 inches. () In a class of students
Name Score Benchmark Test 1 Math Course 1 For use after Lesson 0 1. (5) A -inch ribbon was cut into four equal lengths. How long was each piece of ribbon? A. 7 inches B. 7 1 inches. () In a class of students
Scarborough Spring 2013 Math Exam I 1. "On my honor, as an Aggie, I have neither given nor received unauthorized aid on this academic work.
 Scarborough Spring 2013 Math 365-501 Exam I 1 Math 365 Exam 1 Spring 2013 Scarborough NEATLY PRINT NAME: STUDENT ID: DATE: "On my honor, as an Aggie, I have neither given nor received unauthorized aid
Scarborough Spring 2013 Math 365-501 Exam I 1 Math 365 Exam 1 Spring 2013 Scarborough NEATLY PRINT NAME: STUDENT ID: DATE: "On my honor, as an Aggie, I have neither given nor received unauthorized aid
THE UNIVERSITY OF BRITISH COLUMBIA. Math 335 Section 201. FINAL EXAM April 13, 2013
 Page 1 of 11 THE UNIVERSITY OF BRITISH COLUMBIA Math 335 Section 201 Calculators are allowed No cell phones or information sheets allowed Exam length is 2 hours and 30 minutes FINAL EXAM April 13, 2013
Page 1 of 11 THE UNIVERSITY OF BRITISH COLUMBIA Math 335 Section 201 Calculators are allowed No cell phones or information sheets allowed Exam length is 2 hours and 30 minutes FINAL EXAM April 13, 2013
Cumulative Test. Name. Score. Show all work on this paper. Please use the Student Reference Guide.
 Name Score Math Course 1 1A 1. Use the numbers 6, 12, and 18 to make two addition facts and two subtraction facts. 12 + 12 12 + 12 12 12 12 12 2. Use the numbers 5, 15, and 75 to make two multiplication
Name Score Math Course 1 1A 1. Use the numbers 6, 12, and 18 to make two addition facts and two subtraction facts. 12 + 12 12 + 12 12 12 12 12 2. Use the numbers 5, 15, and 75 to make two multiplication
Practice Test. 2 What is the area of this figure?
 Practice Test 1 Which letter has a line of symmetry? S J R W L 3 Jane's house has a garden which is in the shape of a square. If each side of the garden is 18 feet then what is the perimeter of the garden?
Practice Test 1 Which letter has a line of symmetry? S J R W L 3 Jane's house has a garden which is in the shape of a square. If each side of the garden is 18 feet then what is the perimeter of the garden?
The next criteria will apply to partial tournaments. Consider the following example:
 Criteria for Assessing a Ranking Method Final Report: Undergraduate Research Assistantship Summer 2003 Gordon Davis: dagojr@email.arizona.edu Advisor: Dr. Russel Carlson One of the many questions that
Criteria for Assessing a Ranking Method Final Report: Undergraduate Research Assistantship Summer 2003 Gordon Davis: dagojr@email.arizona.edu Advisor: Dr. Russel Carlson One of the many questions that
Simplifying Radical Expressions and the Distance Formula
 1 RD. Simplifying Radical Expressions and the Distance Formula In the previous section, we simplified some radical expressions by replacing radical signs with rational exponents, applying the rules of
1 RD. Simplifying Radical Expressions and the Distance Formula In the previous section, we simplified some radical expressions by replacing radical signs with rational exponents, applying the rules of
Abstract In this paper, the author deals with the properties of circumscribed ellipses of convex quadrilaterals, using tools of parallel projective tr
 Study on the Properties of Circumscribed Ellipses of Convex Quadrilaterals Author: Yixi Shen Mentors: Zhongyuan Dai; Yijun Yao No. High School of East China Normal University Shanghai, China December,
Study on the Properties of Circumscribed Ellipses of Convex Quadrilaterals Author: Yixi Shen Mentors: Zhongyuan Dai; Yijun Yao No. High School of East China Normal University Shanghai, China December,
Regional winter Tournament Saint Nicholas Thaumaturge - Bourgas
 Regional winter Tournament Saint Nicholas Thaumaturge - Bourgas Area: Mathematics and Information Technologies Style of the Competition: Test exam with multiple-choice and free answers and a problem for
Regional winter Tournament Saint Nicholas Thaumaturge - Bourgas Area: Mathematics and Information Technologies Style of the Competition: Test exam with multiple-choice and free answers and a problem for
The field of play must be rectangular and marked with lines. These lines belong to the areas of which they are boundaries.
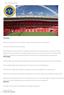 LAW 1: THE FIELD OF PLAY Field surface Matches may be played on natural or artificial surfaces, according to the rules of the competition The colour of artificial surfaces must be green. Where artificial
LAW 1: THE FIELD OF PLAY Field surface Matches may be played on natural or artificial surfaces, according to the rules of the competition The colour of artificial surfaces must be green. Where artificial
Cumulative Test. Name. Score. Show all work on this paper. Please use the Student Reference Guide.
 Name Score Math Course 1 1B 1. Use the numbers 5, 11, and 16 to make two addition facts and two subtraction facts. 11 + 12 12 + 12 12 12 12 12 2. Use the numbers 4, 16, and 64 to make two multiplication
Name Score Math Course 1 1B 1. Use the numbers 5, 11, and 16 to make two addition facts and two subtraction facts. 11 + 12 12 + 12 12 12 12 12 2. Use the numbers 4, 16, and 64 to make two multiplication
2011 Excellence in Mathematics Contest Team Project Level I (Precalculus and above)
 011 Excellence in Mathematics Contest Team Project Level I (Precalculus and above) School Name: Solutions Group Members: Reference Sheet Formulas and Facts You may need to use some of the following formulas
011 Excellence in Mathematics Contest Team Project Level I (Precalculus and above) School Name: Solutions Group Members: Reference Sheet Formulas and Facts You may need to use some of the following formulas
1 8 Practice Perimeter Circumference And Area Answers Form G
 1 8 Practice Perimeter Circumference And Area Answers Form G We have made it easy for you to find a PDF Ebooks without any digging. And by having access to our ebooks online or by storing it on your computer,
1 8 Practice Perimeter Circumference And Area Answers Form G We have made it easy for you to find a PDF Ebooks without any digging. And by having access to our ebooks online or by storing it on your computer,
THE UNIVERSITY OF BRITISH COLUMBIA. Mathematics 414 Section 201. FINAL EXAM December 9, 2011
 Page 1 of 11 THE UNIVERSITY OF BRITISH COLUMBIA Mathematics 414 Section 201 No calculators allowed Final exam begins at 12 noon and ends at 2:30 pm FINAL EXAM December 9, 2011 NAME STUDENT NUMBER Page
Page 1 of 11 THE UNIVERSITY OF BRITISH COLUMBIA Mathematics 414 Section 201 No calculators allowed Final exam begins at 12 noon and ends at 2:30 pm FINAL EXAM December 9, 2011 NAME STUDENT NUMBER Page
2018 School Competition Sprint Round Problems 1 30
 Name 08 School Competition Sprint Round Problems 0 0 4 5 6 7 8 DO NOT BEGIN UNTIL YOU ARE INSTRUCTED TO DO SO. 9 This section of the competition consists of 0 problems. You will have 40 minutes to complete
Name 08 School Competition Sprint Round Problems 0 0 4 5 6 7 8 DO NOT BEGIN UNTIL YOU ARE INSTRUCTED TO DO SO. 9 This section of the competition consists of 0 problems. You will have 40 minutes to complete
13.7 Quadratic Equations and Problem Solving
 13.7 Quadratic Equations and Problem Solving Learning Objectives: A. Solve problems that can be modeled by quadratic equations. Key Vocabulary: Pythagorean Theorem, right triangle, hypotenuse, leg, sum,
13.7 Quadratic Equations and Problem Solving Learning Objectives: A. Solve problems that can be modeled by quadratic equations. Key Vocabulary: Pythagorean Theorem, right triangle, hypotenuse, leg, sum,
ROUND TOSS-UP: What is the square root of one million? (1000) (10 points) BONUS: How many zeros are at the end of ?
 ROUND 1 1. TOSS-UP: What is 24% of 50? (12) (10 points) BONUS: A clothing store is having a 60% off sale on its dresses. Brandi has a coupon that lets her take 20% off of the sale price. If she pays $24
ROUND 1 1. TOSS-UP: What is 24% of 50? (12) (10 points) BONUS: A clothing store is having a 60% off sale on its dresses. Brandi has a coupon that lets her take 20% off of the sale price. If she pays $24
Regional Final. Supervisor s Booklet
 Regional Final Supervisor s Booklet Please ensure that students do not have access to this booklet, and take care to hold it so that answers cannot be seen. Mini-Relay Score Sheet School number: School
Regional Final Supervisor s Booklet Please ensure that students do not have access to this booklet, and take care to hold it so that answers cannot be seen. Mini-Relay Score Sheet School number: School
2011 Excellence in Mathematics Contest Team Project Level I (Precalculus and above) School Name: Group Members:
 011 Excellence in Mathematics Contest Team Project Level I (Precalculus and above) School Name: Group Members: Reference Sheet Formulas and Facts You may need to use some of the following formulas and
011 Excellence in Mathematics Contest Team Project Level I (Precalculus and above) School Name: Group Members: Reference Sheet Formulas and Facts You may need to use some of the following formulas and
2013 Excellence in Mathematics Contest Team Project Level I (Precalculus and above) School Name: Group Members:
 013 Excellence in Mathematics Contest Team Project Level I (Precalculus and above) School Name: Group Members: Reference Sheet Formulas and Facts You may need to use some of the following formulas and
013 Excellence in Mathematics Contest Team Project Level I (Precalculus and above) School Name: Group Members: Reference Sheet Formulas and Facts You may need to use some of the following formulas and
2013 Grade 6 Mathematics Set B
 2013 Grade 6 Mathematics Set B Copyright National Institute for Educational Policy Reserch All Right Reserved URL: https://www.nier.go.jp/english/index.html The English translation is prepared by the Project
2013 Grade 6 Mathematics Set B Copyright National Institute for Educational Policy Reserch All Right Reserved URL: https://www.nier.go.jp/english/index.html The English translation is prepared by the Project
MATHCOUNTS 2005 State Competition Target Round Problems 1 and 2
 MATHCOUNTS 2005 State Competition Target Round Problems 1 and 2 Name School Chapter DO NOT BEGIN UNTIL YOU ARE INSTRUCTED TO DO SO. This round of the competition consists of eight problems, which will
MATHCOUNTS 2005 State Competition Target Round Problems 1 and 2 Name School Chapter DO NOT BEGIN UNTIL YOU ARE INSTRUCTED TO DO SO. This round of the competition consists of eight problems, which will
8-1. The Pythagorean Theorem and Its Converse. Vocabulary. Review. Vocabulary Builder. Use Your Vocabulary
 8-1 he Pythagorean heorem and Its Converse Vocabulary Review 1. Write the square and the positive square root of each number. Number Square Positive Square Root 9 81 3 1 4 1 16 1 2 Vocabulary Builder leg
8-1 he Pythagorean heorem and Its Converse Vocabulary Review 1. Write the square and the positive square root of each number. Number Square Positive Square Root 9 81 3 1 4 1 16 1 2 Vocabulary Builder leg
Candidate Number. General Certificate of Secondary Education Foundation Tier January 2013
 Centre Number Surname Candidate Number For Examiner s Use Other Names Candidate Signature Examiner s Initials General Certificate of Secondary Education Foundation Tier January 2013 Pages 3 4 5 Mark Mathematics
Centre Number Surname Candidate Number For Examiner s Use Other Names Candidate Signature Examiner s Initials General Certificate of Secondary Education Foundation Tier January 2013 Pages 3 4 5 Mark Mathematics
Revision 7/2/02 MEASURING WRAVMA DRAWING DESIGNS WITH SCORING TEMPLATES
 Revision 7/2/02 MEASURING WRAVMA DRAWING DESIGNS WITH SCORING TEMPLATES -these suggested criteria supplement the criteria in the WRAVMA manual *Note item designs depicted here are representational and
Revision 7/2/02 MEASURING WRAVMA DRAWING DESIGNS WITH SCORING TEMPLATES -these suggested criteria supplement the criteria in the WRAVMA manual *Note item designs depicted here are representational and
Unit 2 Day 4 Notes Law of Sines
 AFM Unit 2 Day 4 Notes Law of Sines Name Date Introduction: When you see the triangle below on the left and someone asks you to find the value of x, you immediately know how to proceed. You call upon your
AFM Unit 2 Day 4 Notes Law of Sines Name Date Introduction: When you see the triangle below on the left and someone asks you to find the value of x, you immediately know how to proceed. You call upon your
(a) Monday (b) Wednesday (c) Thursday (d) Friday (e) Saturday
 Middle School Mathematics Competition - Practice Test A Delta College 1. If x > 0, y > 0, z < 0, and x + 2y = m, then z 3 m 2 is (a) always negative (b) always positive (c) zero (d) sometimes negative
Middle School Mathematics Competition - Practice Test A Delta College 1. If x > 0, y > 0, z < 0, and x + 2y = m, then z 3 m 2 is (a) always negative (b) always positive (c) zero (d) sometimes negative
1 8 Practice Perimeter Circumference And Area Form K Answers
 1 8 Practice Perimeter Circumference And Area Form K Answers We have made it easy for you to find a PDF Ebooks without any digging. And by having access to our ebooks online or by storing it on your computer,
1 8 Practice Perimeter Circumference And Area Form K Answers We have made it easy for you to find a PDF Ebooks without any digging. And by having access to our ebooks online or by storing it on your computer,
Learning Objectives Source/Example Questions
 Grade and Strand Learning Objectives Source/Example Questions.ca Ascent Education: http://questions.ascenteducatio n.com.ca A tree 66 meters high casts a 44-meter shadow. Find the angle of elevation of
Grade and Strand Learning Objectives Source/Example Questions.ca Ascent Education: http://questions.ascenteducatio n.com.ca A tree 66 meters high casts a 44-meter shadow. Find the angle of elevation of
Summer Work. 6 th Grade Enriched Math to 7 th Grade Pre-Algebra
 Summer Work 6 th Grade Enriched Math to 7 th Grade Pre-Algebra Attached is a packet for Summer 2017. Take your time. Do not wait until the weeks right before school to begin. The benefit of summer work
Summer Work 6 th Grade Enriched Math to 7 th Grade Pre-Algebra Attached is a packet for Summer 2017. Take your time. Do not wait until the weeks right before school to begin. The benefit of summer work
Name: Date: Period: Score: Rotational Symmetry
 Rotational Symmetry Symmetry: Symmetry is the property of a shape that allows it to be carried onto itself either by by reflection, or rotation. The second kind of symmetry is called rotational symmetry.
Rotational Symmetry Symmetry: Symmetry is the property of a shape that allows it to be carried onto itself either by by reflection, or rotation. The second kind of symmetry is called rotational symmetry.
8-1. The Pythagorean Theorem and Its Converse. Vocabulary. Review. Vocabulary Builder. Use Your Vocabulary
 8-1 The Pythagorean Theorem and Its Converse Vocabulary Review 1. Write the square and the positive square root of each number. Number 9 Square Positive Square Root 1 4 1 16 Vocabulary Builder leg (noun)
8-1 The Pythagorean Theorem and Its Converse Vocabulary Review 1. Write the square and the positive square root of each number. Number 9 Square Positive Square Root 1 4 1 16 Vocabulary Builder leg (noun)
1ACE Exercise 4. Name Date Class
 1ACE Exercise 4 Investigation 1 4. A farm wants to add a small rectangular petting zoo for the public. They have a fixed amount of fencing to use for the zoo. This graph shows the lengths and areas of
1ACE Exercise 4 Investigation 1 4. A farm wants to add a small rectangular petting zoo for the public. They have a fixed amount of fencing to use for the zoo. This graph shows the lengths and areas of
SQUARE ROOTS. Pythagoras theorem has been a perennially interesting. Drawing A SPIRAL OF. ClassRoom
 Drawing A SPIRAL OF SQUARE ROOTS ClassRoom KHUSHBOO AWASTHI "Mathematics possesses a beauty cold and austere, yet sublimely pure, and capable of a stern perfection such as only the greatest art can show."
Drawing A SPIRAL OF SQUARE ROOTS ClassRoom KHUSHBOO AWASTHI "Mathematics possesses a beauty cold and austere, yet sublimely pure, and capable of a stern perfection such as only the greatest art can show."
In previous examples of trigonometry we were limited to right triangles. Now let's see how trig works in oblique (not right) triangles.
 The law of sines. In previous examples of trigonometry we were limited to right triangles. Now let's see how trig works in oblique (not right) triangles. You may recall from Plane Geometry that if you
The law of sines. In previous examples of trigonometry we were limited to right triangles. Now let's see how trig works in oblique (not right) triangles. You may recall from Plane Geometry that if you
Advanced Hydraulics Prof. Dr. Suresh A. Kartha Department of Civil Engineering Indian Institute of Technology, Guwahati
 Advanced Hydraulics Prof. Dr. Suresh A. Kartha Department of Civil Engineering Indian Institute of Technology, Guwahati Module - 4 Hydraulics Jumps Lecture - 4 Features of Hydraulic Jumps (Refer Slide
Advanced Hydraulics Prof. Dr. Suresh A. Kartha Department of Civil Engineering Indian Institute of Technology, Guwahati Module - 4 Hydraulics Jumps Lecture - 4 Features of Hydraulic Jumps (Refer Slide
Parametric Ball Toss TEACHER NOTES MATH NSPIRED. Math Objectives. Vocabulary. About the Lesson. TI-Nspire Navigator System
 Math Objectives Students will be able to use parametric equations to represent the height of a ball as a function of time as well as the path of a ball that has been thrown straight up. Students will be
Math Objectives Students will be able to use parametric equations to represent the height of a ball as a function of time as well as the path of a ball that has been thrown straight up. Students will be
Mark Scheme (Results) Summer 2009
 Mark Scheme (Results) Summer 2009 GCSE GCSE Mathematics (Linear) - 1380 Paper: 1380_2F 2 NOTES ON MARKING PRINCIPLES 1 Types of mark M marks: method marks A marks: accuracy marks B marks: unconditional
Mark Scheme (Results) Summer 2009 GCSE GCSE Mathematics (Linear) - 1380 Paper: 1380_2F 2 NOTES ON MARKING PRINCIPLES 1 Types of mark M marks: method marks A marks: accuracy marks B marks: unconditional
2.6 Related Rates Worksheet Calculus AB. dy /dt!when!x=8
 Two Rates That Are Related(1-7) In exercises 1-2, assume that x and y are both differentiable functions of t and find the required dy /dt and dx /dt. Equation Find Given 1. dx /dt = 10 y = x (a) dy /dt
Two Rates That Are Related(1-7) In exercises 1-2, assume that x and y are both differentiable functions of t and find the required dy /dt and dx /dt. Equation Find Given 1. dx /dt = 10 y = x (a) dy /dt
SAMPLE RH = P 1. where. P 1 = the partial pressure of the water vapor at the dew point temperature of the mixture of dry air and water vapor
 moisture starts to condense out of the air. The temperature at which this happens is called the dew point temperature, or the saturation temperature. What is commonly called saturation pressure or condensing
moisture starts to condense out of the air. The temperature at which this happens is called the dew point temperature, or the saturation temperature. What is commonly called saturation pressure or condensing
Lecture 1: Knot Theory
 Math 7H Professor: Padraic Bartlett Lecture 1: Knot Theory Week 1 UCSB 015 1 Introduction Outside of mathematics, knots are ways to loop a single piece of string around itself: In mathematics, we mean
Math 7H Professor: Padraic Bartlett Lecture 1: Knot Theory Week 1 UCSB 015 1 Introduction Outside of mathematics, knots are ways to loop a single piece of string around itself: In mathematics, we mean
Extensive Games with Perfect Information
 Extensive Games with Perfect Information A strategic situation in which players play a game over time. At the point of making the decision, players are informed about the action chosen before by the others.
Extensive Games with Perfect Information A strategic situation in which players play a game over time. At the point of making the decision, players are informed about the action chosen before by the others.
5. Find two numbers whose sum is 48 and whose product is to be a maximum.
 1 Optimization Practice (4.4) 1. If 40 passengers hire a special car on a train, they will be charged $8 each. This fare will be reduced by $.10 each passenger, for each person in addition to these 40.
1 Optimization Practice (4.4) 1. If 40 passengers hire a special car on a train, they will be charged $8 each. This fare will be reduced by $.10 each passenger, for each person in addition to these 40.
Rules for the Mental Calculation World Cup 2018
 Rules for the Mental Calculation World Cup 2018 General Information The entry form and more information about the event can be downloaded from www.recordholders.org/en/events/worldcup/. Registration and
Rules for the Mental Calculation World Cup 2018 General Information The entry form and more information about the event can be downloaded from www.recordholders.org/en/events/worldcup/. Registration and
Chapter 7. Right Triangles and Trigonometry
 Chapter 7 Right Triangles and Trigonometry 4 16 25 100 144 LEAVE IN RADICAL FORM Perfect Square Factor * Other Factor 8 20 32 = = = 4 *2 = = = 75 = = 40 = = 7.1 Apply the Pythagorean Theorem Objective:
Chapter 7 Right Triangles and Trigonometry 4 16 25 100 144 LEAVE IN RADICAL FORM Perfect Square Factor * Other Factor 8 20 32 = = = 4 *2 = = = 75 = = 40 = = 7.1 Apply the Pythagorean Theorem Objective:
Design, Operation and Maintenance of a Swimming Pool
 Page 1 of 2 WASHINGTON STATE MATHEMATICS COUNCIL 2018 MIDDLE SCHOOL MATH OLYMPIAD Session I: PROBLEM SOLVING Design, Operation and Maintenance of a Swimming Pool The City is planning to build a swimming
Page 1 of 2 WASHINGTON STATE MATHEMATICS COUNCIL 2018 MIDDLE SCHOOL MATH OLYMPIAD Session I: PROBLEM SOLVING Design, Operation and Maintenance of a Swimming Pool The City is planning to build a swimming
Edexcel GCSE. Mathematics A 1387 Paper 5523/03. November Mark Scheme. Mathematics A 1387
 Edexcel GCSE Mathematics A 187 Paper 552/0 November 2007 Mark Scheme Edexcel GCSE Mathematics A 187 NOTES ON MARKING PRINCIPLES 1 Types of mark M marks: method marks A marks: accuracy marks B marks: unconditional
Edexcel GCSE Mathematics A 187 Paper 552/0 November 2007 Mark Scheme Edexcel GCSE Mathematics A 187 NOTES ON MARKING PRINCIPLES 1 Types of mark M marks: method marks A marks: accuracy marks B marks: unconditional
Monday Tuesday Wednesday Thursday
 Name: Weekly Math Homework - Q1:1 Teacher: Monday Tuesday Wednesday Thursday Use Order of Operations to simplify. Use Order of Operations to simplify. Use Order of Operations to simplify. Use Order of
Name: Weekly Math Homework - Q1:1 Teacher: Monday Tuesday Wednesday Thursday Use Order of Operations to simplify. Use Order of Operations to simplify. Use Order of Operations to simplify. Use Order of
AP Physics 1 Summer Packet Review of Trigonometry used in Physics
 AP Physics 1 Summer Packet Review of Trigonometry used in Physics For some of you this material will seem pretty familiar and you will complete it quickly. For others, you may not have had much or any
AP Physics 1 Summer Packet Review of Trigonometry used in Physics For some of you this material will seem pretty familiar and you will complete it quickly. For others, you may not have had much or any
Design, Operation and Maintenance of a Swimming Pool
 Page 1 of 2 WASHINGTON STATE MATHEMATICS COUNCIL 2018 MIDDLE SCHOOL MATH OLYMPIAD Session I: PROBLEM SOLVING Design, Operation and Maintenance of a Swimming Pool The City is planning to build a swimming
Page 1 of 2 WASHINGTON STATE MATHEMATICS COUNCIL 2018 MIDDLE SCHOOL MATH OLYMPIAD Session I: PROBLEM SOLVING Design, Operation and Maintenance of a Swimming Pool The City is planning to build a swimming
Math is Cool Masters
 Sponsored by: American Chemical Society Individual Contest Written by Cherie Clymer GENERAL INSTRUCTIONS Good sportsmanship is expected throughout the competition by all involved. Bad sportsmanship may
Sponsored by: American Chemical Society Individual Contest Written by Cherie Clymer GENERAL INSTRUCTIONS Good sportsmanship is expected throughout the competition by all involved. Bad sportsmanship may
Optimal Weather Routing Using Ensemble Weather Forecasts
 Optimal Weather Routing Using Ensemble Weather Forecasts Asher Treby Department of Engineering Science University of Auckland New Zealand Abstract In the United States and the United Kingdom it is commonplace
Optimal Weather Routing Using Ensemble Weather Forecasts Asher Treby Department of Engineering Science University of Auckland New Zealand Abstract In the United States and the United Kingdom it is commonplace
21-110: Problem Solving in Recreational Mathematics
 21-110: Problem Solving in Recreational Mathematics Homework assignment 1 solutions Problem 1. Find my office. Sign your name on the sheet posted outside my office door. Solution. My office is in the Physical
21-110: Problem Solving in Recreational Mathematics Homework assignment 1 solutions Problem 1. Find my office. Sign your name on the sheet posted outside my office door. Solution. My office is in the Physical
OKLAHOMA MATH DAY. Instructions for the SOONER MATH BOWL
 OKLAHOMA MATH DAY NOVEMBER 16, 2002 Instructions for the SOONER MATH BOWL 1. The team event will be run in three stages. 2. Each team may have 3 5 students and a school can send in as many teams as they
OKLAHOMA MATH DAY NOVEMBER 16, 2002 Instructions for the SOONER MATH BOWL 1. The team event will be run in three stages. 2. Each team may have 3 5 students and a school can send in as many teams as they
Figure 5.1: molecular interaction
 Chapter 5 Surface tension 5.1 Definition If a line element be imagined on the surface of a liquid in any direction, the surface tension of the liquid, at a given temperature, is defined as the force per
Chapter 5 Surface tension 5.1 Definition If a line element be imagined on the surface of a liquid in any direction, the surface tension of the liquid, at a given temperature, is defined as the force per
5.1. Data Displays Batter Up. My Notes ACTIVITY
 SUGGESTED LEARNING STRATEGIES: Activating Prior Knowledge, Marking the Text, Group Presentation, Interactive Word Wall Henry Hank Aaron and Harmon Killebrew are among the alltime leaders in home runs in
SUGGESTED LEARNING STRATEGIES: Activating Prior Knowledge, Marking the Text, Group Presentation, Interactive Word Wall Henry Hank Aaron and Harmon Killebrew are among the alltime leaders in home runs in
Section 8: Right Triangles
 The following Mathematics Florida Standards will be covered in this section: MAFS.912.G-CO.2.8 Explain how the criteria for triangle congruence (ASA, SAS, SSS, and Hypotenuse-Leg) follow from the definition
The following Mathematics Florida Standards will be covered in this section: MAFS.912.G-CO.2.8 Explain how the criteria for triangle congruence (ASA, SAS, SSS, and Hypotenuse-Leg) follow from the definition
ECO 199 GAMES OF STRATEGY Spring Term 2004 Precept Materials for Week 3 February 16, 17
 ECO 199 GAMES OF STRATEGY Spring Term 2004 Precept Materials for Week 3 February 16, 17 Illustration of Rollback in a Decision Problem, and Dynamic Games of Competition Here we discuss an example whose
ECO 199 GAMES OF STRATEGY Spring Term 2004 Precept Materials for Week 3 February 16, 17 Illustration of Rollback in a Decision Problem, and Dynamic Games of Competition Here we discuss an example whose
γ water = 62.4 lb/ft 3 = 9800 N/m 3
 CEE 4 Aut 004, Exam # Work alone. Answer all questions. Total pts: 90. Always make your thought process clear; if it is not, you will not receive partial credit for incomplete or partially incorrect answers.
CEE 4 Aut 004, Exam # Work alone. Answer all questions. Total pts: 90. Always make your thought process clear; if it is not, you will not receive partial credit for incomplete or partially incorrect answers.
Calculation of Trail Usage from Counter Data
 1. Introduction 1 Calculation of Trail Usage from Counter Data 1/17/17 Stephen Martin, Ph.D. Automatic counters are used on trails to measure how many people are using the trail. A fundamental question
1. Introduction 1 Calculation of Trail Usage from Counter Data 1/17/17 Stephen Martin, Ph.D. Automatic counters are used on trails to measure how many people are using the trail. A fundamental question
CMIMC 2018 Official Contest Information
 CMIMC 2018 Official Contest Information CMIMC Staff Latest version: January 14, 2018 1 Introduction 1. This document is the official contest information packet for the 2018 Carnegie Mellon Informatics
CMIMC 2018 Official Contest Information CMIMC Staff Latest version: January 14, 2018 1 Introduction 1. This document is the official contest information packet for the 2018 Carnegie Mellon Informatics
Louis M. Edwards Mathematics Super Bowl Valencia Community College -- April 19, 2002
 Practice Round 1. At Wakeel s Pizza Emporium, large pizzas (14 diameter round) cost $9.99, extra large pizzas (16 diameter round) cost $13.99 and super large pizzas (18 diameter round) cost $16.99. What
Practice Round 1. At Wakeel s Pizza Emporium, large pizzas (14 diameter round) cost $9.99, extra large pizzas (16 diameter round) cost $13.99 and super large pizzas (18 diameter round) cost $16.99. What
MI 4 Project on Parametric Equations. Parametric Worksheet
 (To be done just before project is assigned.) Parametric Worksheet 1. From its initial position at (3,4), an object moves linearly, reaching (9, 8) after two seconds and (15, 12) after four seconds. a.
(To be done just before project is assigned.) Parametric Worksheet 1. From its initial position at (3,4), an object moves linearly, reaching (9, 8) after two seconds and (15, 12) after four seconds. a.
The Coach then sorts the 25 players into separate teams and positions
 Section 4 A: Contingency Tables Introduction A local school has a Varsity and Junior Varsity basketball team. No player plays on both teams and no player plays at more than one position. The coach writes
Section 4 A: Contingency Tables Introduction A local school has a Varsity and Junior Varsity basketball team. No player plays on both teams and no player plays at more than one position. The coach writes
CH 34 MORE PYTHAGOREAN THEOREM AND RECTANGLES
 CH 34 MORE PYTHAGOREAN THEOREM AND RECTANGLES 317 Recalling The Pythagorean Theorem a 2 + b 2 = c 2 a c 90 b The 90 angle is called the right angle of the right triangle. The other two angles of the right
CH 34 MORE PYTHAGOREAN THEOREM AND RECTANGLES 317 Recalling The Pythagorean Theorem a 2 + b 2 = c 2 a c 90 b The 90 angle is called the right angle of the right triangle. The other two angles of the right
Bridge Decomposition of Restriction Measures Tom Alberts joint work with Hugo Duminil (ENS) with lots of help from Wendelin Werner University of
 Bridge Decomposition of Restriction Measures Tom Alberts joint work with Hugo Duminil (ENS) with lots of help from Wendelin Werner University of Toronto Self-Avoiding Walk Bridges Self-Avoiding Walk Bridges
Bridge Decomposition of Restriction Measures Tom Alberts joint work with Hugo Duminil (ENS) with lots of help from Wendelin Werner University of Toronto Self-Avoiding Walk Bridges Self-Avoiding Walk Bridges
GCSE Mathematics Calculator Foundation Tier Free Practice Set 5 1 hour 30 minutes ANSWERS. Marks shown in brackets for each question (2)
 MathsMadeEasy 3 GCSE Mathematics Calculator Foundation Tier Free Practice Set 5 1 hour 30 minutes ANSWERS Marks shown in brackets for each question Typical Grade Boundaries C D E F G 76 60 47 33 20 Legend
MathsMadeEasy 3 GCSE Mathematics Calculator Foundation Tier Free Practice Set 5 1 hour 30 minutes ANSWERS Marks shown in brackets for each question Typical Grade Boundaries C D E F G 76 60 47 33 20 Legend
Unit 4. Triangle Relationships. Oct 3 8:20 AM. Oct 3 8:21 AM. Oct 3 8:26 AM. Oct 3 8:28 AM. Oct 3 8:27 AM. Oct 3 8:27 AM
 Unit 4 Triangle Relationships 4.1 -- Classifying Triangles triangle -a figure formed by three segments joining three noncollinear points Classification of triangles: by sides by angles Oct 3 8:20 AM Oct
Unit 4 Triangle Relationships 4.1 -- Classifying Triangles triangle -a figure formed by three segments joining three noncollinear points Classification of triangles: by sides by angles Oct 3 8:20 AM Oct
Chapter 11 Waves. Waves transport energy without transporting matter. The intensity is the average power per unit area. It is measured in W/m 2.
 Energy can be transported by particles or waves: Chapter 11 Waves A wave is characterized as some sort of disturbance that travels away from a source. The key difference between particles and waves is
Energy can be transported by particles or waves: Chapter 11 Waves A wave is characterized as some sort of disturbance that travels away from a source. The key difference between particles and waves is
You are to develop a program that takes as input the scorecard filled out by Bob and that produces as output the correct scorecard.
 Problem 1: What s My Score? Ann, Bob, Carol, and Dave played nine holes of golf together. On the first hole, Ann teed off first, followed by Bob, then Carol, and, finally, Dave. At each subsequent hole,
Problem 1: What s My Score? Ann, Bob, Carol, and Dave played nine holes of golf together. On the first hole, Ann teed off first, followed by Bob, then Carol, and, finally, Dave. At each subsequent hole,
CH 21 THE PYTHAGOREAN THEOREM
 121 CH 21 THE PYTHAGOREAN THEOREM The Right Triangle A n angle of 90 is called a right angle, and when two things meet at a right angle, we say they are perpendicular. For example, the angle between a
121 CH 21 THE PYTHAGOREAN THEOREM The Right Triangle A n angle of 90 is called a right angle, and when two things meet at a right angle, we say they are perpendicular. For example, the angle between a
11 TH ANNUAL MATHLETES IN ACTION
 11 TH ANNUAL MATHLETES IN ACTION NOVEMBER 8, 2014 SPRINT ROUND PROBLEMS 1-25 NAME SCHOOL DO NOT BEGIN UNTIL INSTRUCTED TO DO SO. This round of the competition consists of twenty-five problems. You will
11 TH ANNUAL MATHLETES IN ACTION NOVEMBER 8, 2014 SPRINT ROUND PROBLEMS 1-25 NAME SCHOOL DO NOT BEGIN UNTIL INSTRUCTED TO DO SO. This round of the competition consists of twenty-five problems. You will
arxiv: v1 [math.co] 11 Apr 2018
![arxiv: v1 [math.co] 11 Apr 2018 arxiv: v1 [math.co] 11 Apr 2018](/thumbs/87/97408575.jpg) arxiv:1804.04504v1 [math.co] 11 Apr 2018 Scheduling Asynchronous Round-Robin Tournaments Warut Suksompong Abstract. We study the problem of scheduling asynchronous round-robin tournaments. We consider
arxiv:1804.04504v1 [math.co] 11 Apr 2018 Scheduling Asynchronous Round-Robin Tournaments Warut Suksompong Abstract. We study the problem of scheduling asynchronous round-robin tournaments. We consider
Fun with Folding. led by Thomas Clark. October 7, Take a strip of paper, fold it in half, and make a good crease at the midpoint position.
 Preliminary Folding Investigation Fun with Folding led by Thomas Clark October 7, 2014 1. Take a strip of paper, fold it in half, and make a good crease at the midpoint position. 2. Open up the strip,
Preliminary Folding Investigation Fun with Folding led by Thomas Clark October 7, 2014 1. Take a strip of paper, fold it in half, and make a good crease at the midpoint position. 2. Open up the strip,
Mathematics 7 WORKBOOK
 EXAM FEVER Mathematics 7 WORKBOOK This book belongs to: Exam Fever Publishers PIETERMARITZBURG www.examfever.co.za Table of Contents TERM 1 Chapter and Topic Page 1. Whole Numbers 1 2. Exponents 15 3.
EXAM FEVER Mathematics 7 WORKBOOK This book belongs to: Exam Fever Publishers PIETERMARITZBURG www.examfever.co.za Table of Contents TERM 1 Chapter and Topic Page 1. Whole Numbers 1 2. Exponents 15 3.
Finding the Area of a Major League Baseball Field
 Undergraduate Journal of Mathematical Modeling: One + Two Volume 5 2012 Fall Issue 1 Article 7 Finding the Area of a Major League Baseball Field Jacob Courchaine University of South Florida Advisors: Arcadii
Undergraduate Journal of Mathematical Modeling: One + Two Volume 5 2012 Fall Issue 1 Article 7 Finding the Area of a Major League Baseball Field Jacob Courchaine University of South Florida Advisors: Arcadii
Gurudwara Road Model Town, Hisar SSC CGL Tier 2
 Gurudwara Road Model Town, Hisar 9729327755 SSC CGL Tier 2 Math Paper code: 7 ------------------------------------------------------------------------------------------------------------------- No. of
Gurudwara Road Model Town, Hisar 9729327755 SSC CGL Tier 2 Math Paper code: 7 ------------------------------------------------------------------------------------------------------------------- No. of
Adding Whole Numbers and Money Subtracting Whole Numbers and Money Fact Families, Part 1
 Adding Whole Numbers and Money Subtracting Whole Numbers and Money Fact Families, Part 1 Reteaching 1 Math Course 1, Lesson 1 To add money, line up the decimal points. Then add each column starting on
Adding Whole Numbers and Money Subtracting Whole Numbers and Money Fact Families, Part 1 Reteaching 1 Math Course 1, Lesson 1 To add money, line up the decimal points. Then add each column starting on
Referee Positioning. Ohio South Referee Recertification Training
 Referee Positioning Ohio South 2017-18 Referee Recertification Training Referee Positioning How to be in the right place at the right time? What is the best position for the referee? Referee Positioning
Referee Positioning Ohio South 2017-18 Referee Recertification Training Referee Positioning How to be in the right place at the right time? What is the best position for the referee? Referee Positioning
Name: Class: Date: Geometry Chapter 4 Test Review
 Name: Class: Date: ID: C Geometry Chapter 4 Test Review. 1. Determine the measure of angle UPM in the following figure. Explain your reasoning and show all your work. 3. Determine the side length of each
Name: Class: Date: ID: C Geometry Chapter 4 Test Review. 1. Determine the measure of angle UPM in the following figure. Explain your reasoning and show all your work. 3. Determine the side length of each
Team 7416 HiMCM 2017 Page 1 of 24. Olympic ski slopes are difficult to plan, and a ranch in Utah is being evaluated to
 Team 7416 HiMCM 2017 Page 1 of 24 Summary Olympic ski slopes are difficult to plan, and a ranch in Utah is being evaluated to determine whether or not it should host an event. The measurements and difficulty
Team 7416 HiMCM 2017 Page 1 of 24 Summary Olympic ski slopes are difficult to plan, and a ranch in Utah is being evaluated to determine whether or not it should host an event. The measurements and difficulty
THE 2018 ROSENTHAL PRIZE for Innovation in Math Teaching. Geometry Project: DARTBOARD
 THE 2018 ROSENTHAL PRIZE for Innovation in Math Teaching Geometry Project: DARTBOARD Geometric Probability Theoretical Probability and Experimental Probability Elizabeth Masslich Geometry grades 6-12 Table
THE 2018 ROSENTHAL PRIZE for Innovation in Math Teaching Geometry Project: DARTBOARD Geometric Probability Theoretical Probability and Experimental Probability Elizabeth Masslich Geometry grades 6-12 Table
Math Talent Test Practice Questions for Grade 5
 Math Talent Test Practice Questions for Grade 5 1. There are 6 yellow balls, 4 red balls, and 5 blue balls in a bag. How many balls do you need to draw from the bag to guarantee that you have a blue ball?
Math Talent Test Practice Questions for Grade 5 1. There are 6 yellow balls, 4 red balls, and 5 blue balls in a bag. How many balls do you need to draw from the bag to guarantee that you have a blue ball?
