Cluster trees and message propagation
|
|
|
- Anne Flowers
- 5 years ago
- Views:
Transcription
1 luste tees and message popagaton 371 Advanced A Tomas ngla Outlne mple gaphs: tees and polytees luste gaphs and clque tees unnng ntesecton sepsetsmessage popagaton VE Message passng VE n detal achng out-of-clque quees P ncemental updatng onstuctng clque tees vaable elmnaton VE and BP: Pos & cons and tadeoffs
2 Tees and polytees Tee: one dected path fom the oot to each node PolyTee: one undected tal fom the oot to each node Undected epesentaton: a tee gaph teewdth1 lque tees VE woks on factos Make facto a data stuctue ends and eceves messages luste gaph fo set of factos each node s assocated wth a subset cluste of. Famly-pesevng: each facto s vaables ae completely embedded n a cluste
3 lque tee popetes epset sepaaton set: Vaables X on one sde of sepset ae sepaated fom the vaables Y on the othe sde n the facto gaph gven vaables n Runnng ntesecton f and both contan X then all clques on the unque path between them do lque tees P P P Runnng ntesecton: lques nvolvng fom a connected subtee. P P P P ntal potentals : Assgn factos to clques and multply them. ave espect fo famles! P Tee need not be mnmal
4 Message Passng VE Quey fo P Elmnate : Message eceved at [] -- [] updates: τ 1 1 [ ] Message sent fom [] to [] [ ] τ1 [ ] Message Passng VE Quey fo P Elmnate : τ [ ] Message eceved at [] -- [] updates: 3[ ] τ 3[ ] Message sent fom [] to []
5 Message Passng VE Quey fo P Elmnate : τ 3 3[ ] Message eceved at [] -- [] updates: Message sent fom [] to [] 4[ ] τ3 4[ ]! [] s not eady! Message Passng VE Quey fo P Elmnate : τ 4 5[ ] Message sent fom [] to [] All messages eceved at [] [] updates: 4[ ] τ3 τ4 4[ ] And so on
6 Message Passng VE hose [] as the oot clque ould we have chosen othewse? Message Passng VE hoose [] as the oot clque Obsevaton: ome messages dd not change! [] [] Notaton: numbe the clques and denote the messages
7 oectness of VE on clque tees Message summazes nfomaton n the pat of tee t sepaates V p φ F p Poof s by nducton fom leaves Base case leaf clque φ φ φ F oectness of VE on clque tees nducton case: non-leaf clque sendng to wth chlden... 1 k φ... φ φ... φ Vp φ F p Y Vp V F k F F 1 p φ φ p 1 φ p k by ntesecton popety the unons ae dsont V Then + p Y UVp m m 1.. k φ F + p F U Fp m m 1.. k φ φ... V p φ F p Y φ F Vp φ F V F 1 p 1 p k φ p k φ
8 oectness of VE on clque tees By nducton hypothess V F p p φ φ Y k m V F m φ φ.. 1 p p X V k k k X hlden hlden X hlden V F X hlden \... φ φ p p Then the oot clque has the coect magnal: Message passng VE Message ode s only patal omputes magnals fo any node Y Results n a calbated clque tee Often many magnals desed neffcent to e-un nfeence One dstnct message pe edge & decton Recap: thee knds of facto obects ntal fnal potentals and messages
9 Message Passng VE hafe-henoy algothm asynchonous mplementaton of two passes: upwad and downwad Asynchonously do: node eady to send m to node when t has eceved a message fom all othe nodes end message Magnalze oot clque s ancllay vas k k N Message Passng: BP aphcal model of a dstbuton Moe edges lage expessve powe lque tee also a model of dstbuton Message passng peseves model but changes paametezaton ffeent but equvalent algothm
10 Facto dvson A1 B1.5 A1 B1.5/.41.5 A1 A A A3 B B1 B B A1 A A A1 A A A3 B B1 B B1.4/.41..8/.4../.4..6/.51. A3 B.5 A3 B.5/.51. nvese of facto poduct Message Passng: BP Each node: multply all the messages and dvde by the one comng fom node we send to lealy the same as VE k k N k k N \
11 Message Passng: BP AB B B B B B B 1 B A B B B B B toe the last message on the edge and dvde each passng message by the last stoed. Message Popagaton: BP autzen-pegelhalte algothm Two knds of obects ntal potentals not kept mpoved stablty of asynchonous algothm epeated messages cancel out stbuton epesentaton clque tee nvaant X P F T T T µ
12 Multple quees Much cachng possble ove a clque tee Example: compute PXY fo each X Y ynamc pogammng Base case X and Y ae n neghbo clques P µ P Take advantage of condtonal ndependence: l l : P P P l l l ncemental updates Fully-nfomed: all neghbos have sent the messages albated -- messages and clques agee on magnals: fxed pont of MP µ Evdence avalable n peces Re-unnng nfeence neffcent Expess evdence n ndcato vecto multply nto some clque un one pass away fom to nfom the est woks fo soft evdence as well
13 Out-of-clque quees want PB no clque wth both B and! Buld a new clque tee expensve o o vaable elmnaton ove calbated tee AB B B P B P B B 3 µ 3 P B P Ths s back to VE we save f vaables of nteest ae close n the clque tee. efnng clque tees VE defnes clques Each facto s subset of a clque of Evey max clque n s a facto Each clque n s a subclque n Each clque n s a clque n Non-maxmal clques can be elmnated hodal gaphs Maxmal clques of any c.g. that s a supeset of can be aanged nto a clque tee fo tangulaton
14 lque tees geneated by VE aph nduced by odeng: VE constuctng a clque tee
15 VE constuctng a clque tee VE constuctng a clque tee
16 VE constuctng a clque tee VE constuctng a clque tee
17 VE constuctng a clque tee VE constuctng a clque tee
18 VE constuctng a clque tee ummay lque tees factos assgned to clques many-to-one unnng ntesecton Message passng on clque tees Vaable Elmnaton Belef popagaton dffeent vews algebacally the same VE defnes clques Tme and space tadeoff spectum
19 Thank you Questons solcted
Motivation. Prize-Collecting Steiner Tree Problem (PCSTP) Kosten und Profite. Das Fraktionale Prize-Collecting Steiner Tree Problem auf Baumgraphen
 Das Faktonale Pze-Collectng Stene Tee Poblem auf Baumgaphen Motvaton Gunna W. Klau (TU Wen Ivana Ljubć (TU Wen Peta Mutzel (Un Dotmund Ulch Pfeschy (Un Gaz René Weskche (TU Wen Motvaton Modell Kosten und
Das Faktonale Pze-Collectng Stene Tee Poblem auf Baumgaphen Motvaton Gunna W. Klau (TU Wen Ivana Ljubć (TU Wen Peta Mutzel (Un Dotmund Ulch Pfeschy (Un Gaz René Weskche (TU Wen Motvaton Modell Kosten und
Noncrossing Trees and Noncrossing Graphs
 Noncossing Tees and Noncossing Gaphs William Y. C. Chen and Shey H. F. Yan Cente fo Combinatoics, LPMC, Nanai Univesity, 300071 Tianjin, P.R. China chen@nanai.edu.cn, huifangyan@eyou.com Submitted: Sep
Noncossing Tees and Noncossing Gaphs William Y. C. Chen and Shey H. F. Yan Cente fo Combinatoics, LPMC, Nanai Univesity, 300071 Tianjin, P.R. China chen@nanai.edu.cn, huifangyan@eyou.com Submitted: Sep
Trees & Routing (1) BFS
 Tees & Routing (1) BFS Why (spanning) tees? Spanning Tee Given a gaph G=(V,E), a Spanning Tee of G is an acyclic subgaph, spanning all the nodes in V. Spanning Tee Given a gaph G=(V,E), a Spanning Tee
Tees & Routing (1) BFS Why (spanning) tees? Spanning Tee Given a gaph G=(V,E), a Spanning Tee of G is an acyclic subgaph, spanning all the nodes in V. Spanning Tee Given a gaph G=(V,E), a Spanning Tee
Depth-first search and strong connectivity in Coq
 1 Depth-fist seach and stong connectivity in Coq Januay 9, 2015 2 The poblem Finding the stongly connected components of a diected gaph. Pedagogical value: The fist nontivial gaph algoithm. Pactical value:
1 Depth-fist seach and stong connectivity in Coq Januay 9, 2015 2 The poblem Finding the stongly connected components of a diected gaph. Pedagogical value: The fist nontivial gaph algoithm. Pactical value:
10 Torque. Lab. What You Need To Know: Physics 211 Lab
 b Lab 10 Toque What You Need To Know: F (a) F F Angula Systems Evey lab up to this point has dealt with objects moving in the linea system. In othe wods, objects moving in a staight line. Now we ae going
b Lab 10 Toque What You Need To Know: F (a) F F Angula Systems Evey lab up to this point has dealt with objects moving in the linea system. In othe wods, objects moving in a staight line. Now we ae going
Domain Decomposition
 Doman Decomposton Paallelzaton of Mesh Based pplcatons Panagots damds Thomas Bönsch Unvesty of Stuttgat Hgh-Pefomance Computng-Cente Stuttgat (HLRS) wwwhlsde Höchstlestungsechenzentum Stuttgat Outlne ntoducton
Doman Decomposton Paallelzaton of Mesh Based pplcatons Panagots damds Thomas Bönsch Unvesty of Stuttgat Hgh-Pefomance Computng-Cente Stuttgat (HLRS) wwwhlsde Höchstlestungsechenzentum Stuttgat Outlne ntoducton
Red-Black Trees Goodrich, Tamassia Red-Black Trees 1
 Red-Black Tees 8 00 Goodich, Tamassia Red-Black Tees 1 Fom (,) to Red-Black Tees A ed-black tee is a epesentation of a (,) tee by means of a binay tee whose nodes ae coloed ed o black In compaison with
Red-Black Tees 8 00 Goodich, Tamassia Red-Black Tees 1 Fom (,) to Red-Black Tees A ed-black tee is a epesentation of a (,) tee by means of a binay tee whose nodes ae coloed ed o black In compaison with
arxiv:cs/ v1 [cs.ds] 8 Dec 1998
![arxiv:cs/ v1 [cs.ds] 8 Dec 1998 arxiv:cs/ v1 [cs.ds] 8 Dec 1998](/thumbs/79/79557328.jpg) Minimum Cuts in Nea-Linea Time David R. Kage Febuay 1, 2008 axiv:cs/9812007v1 [cs.ds] 8 Dec 1998 Abstact We significantly impove known time bounds fo solving the minimum cut poblem on undiected gaphs.
Minimum Cuts in Nea-Linea Time David R. Kage Febuay 1, 2008 axiv:cs/9812007v1 [cs.ds] 8 Dec 1998 Abstact We significantly impove known time bounds fo solving the minimum cut poblem on undiected gaphs.
Forschungszentrum Karlsruhe Technik und Umwelt. LINEFIT concept. Problem: Transition from measured transmission spectrum to ILS.
 LINEFI concept Poblem: anston om measued tansmsson spectum to ILS.0 400 0.9 300 tansmsson 0.8 0.7 esponse [cm] 00 00 0.6 0 76.94 76.96 76.98 77.00 77.0 wae numbe [cm - ] -0.030-0.05 0.000 0.05 0.030 wae
LINEFI concept Poblem: anston om measued tansmsson spectum to ILS.0 400 0.9 300 tansmsson 0.8 0.7 esponse [cm] 00 00 0.6 0 76.94 76.96 76.98 77.00 77.0 wae numbe [cm - ] -0.030-0.05 0.000 0.05 0.030 wae
Using Origami to Find Rational Approximations of Irrational Roots
 Usng Ogam to Fnd Ratonal Appomatons of Iatonal Roots Jeemy Lee Amest Regonal Hg Sool Hudson Rve Undegaduate Matemats Confeene Wllams College Apl 6 t, 0 Ogam Instutons Foldng pape allows us to fnd atonal
Usng Ogam to Fnd Ratonal Appomatons of Iatonal Roots Jeemy Lee Amest Regonal Hg Sool Hudson Rve Undegaduate Matemats Confeene Wllams College Apl 6 t, 0 Ogam Instutons Foldng pape allows us to fnd atonal
British Prime Minister Benjamin Disraeli once remarked that
 GABREL COSTA, MCHAEL HUBER, & OHN SACCOMAN Cumulative Home Run Fequency and the Recent Home Run Explosion Bitish Pime Ministe Benjamin Disaeli once emaked that thee ae thee kinds of falsehoods: lies, damned
GABREL COSTA, MCHAEL HUBER, & OHN SACCOMAN Cumulative Home Run Fequency and the Recent Home Run Explosion Bitish Pime Ministe Benjamin Disaeli once emaked that thee ae thee kinds of falsehoods: lies, damned
Lesson 33: Horizontal & Vertical Circular Problems
 Lesson 33: Hoizontal & Vetical Cicula Poblems Thee ae a wide vaiety of questions that you do if you apply you knowledge of cicula motion coectly. The tough pat is figuing out how to set them up. You need
Lesson 33: Hoizontal & Vetical Cicula Poblems Thee ae a wide vaiety of questions that you do if you apply you knowledge of cicula motion coectly. The tough pat is figuing out how to set them up. You need
Tree. Tree. Siblings Grand Parent Grand Child H I J I J K. Tree Definitions
 Tee Tee Lectues : oontee Kuatachue Room no. Kitawan Siiboon Room no. Text : ata Stuctues & lgoithm nalysis in, ++, Mak llen Weiss, ddison Wesley. Tee efinitions. inay Tee Tavesals inay Seach Tee Repesentations
Tee Tee Lectues : oontee Kuatachue Room no. Kitawan Siiboon Room no. Text : ata Stuctues & lgoithm nalysis in, ++, Mak llen Weiss, ddison Wesley. Tee efinitions. inay Tee Tavesals inay Seach Tee Repesentations
Traditional Rendering Radiosity
 Tadtonal Rndng Radost CS 57 all 00 Comput Scnc Conll Unvst Hsto Poblms wth classc a tacng: ot alstc: onl pfct spcula and pfct factv/flcton btwn sufacs Vw-dpndnt Radost 984 Global Illumnaton n dffus scns
Tadtonal Rndng Radost CS 57 all 00 Comput Scnc Conll Unvst Hsto Poblms wth classc a tacng: ot alstc: onl pfct spcula and pfct factv/flcton btwn sufacs Vw-dpndnt Radost 984 Global Illumnaton n dffus scns
Multi-Robot Forest Coverage
 Multi-Robot Foest Coveage Xiaoming Zheng Sonal Jain Sven Koenig David Kempe Depatment of Compute Science Univesity of Southen Califonia Los Angeles, CA 90089-0781, USA {xiaominz, sonaljai, skoenig, dkempe}@usc.edu
Multi-Robot Foest Coveage Xiaoming Zheng Sonal Jain Sven Koenig David Kempe Depatment of Compute Science Univesity of Southen Califonia Los Angeles, CA 90089-0781, USA {xiaominz, sonaljai, skoenig, dkempe}@usc.edu
Faster Nearest Neighbors: Voronoi Diagrams and k-d Trees
 154 25 Jonathan Richad Shewchuk Faste Neaest Neighbos: Voonoi Diagams and k-d Tees SPEEDING UP NEAREST NEIGHBOR CLASSIFIERS Can we pepocess taining pts to obtain sublinea quey time? 2 5 dimensions: Voonoi
154 25 Jonathan Richad Shewchuk Faste Neaest Neighbos: Voonoi Diagams and k-d Tees SPEEDING UP NEAREST NEIGHBOR CLASSIFIERS Can we pepocess taining pts to obtain sublinea quey time? 2 5 dimensions: Voonoi
Torque. Physics 2. Prepared by Vince Zaccone For Campus Learning Assistance Services at UCSB
 Toque Physics Toque Toque is what causes angula acceleation (just like a foce causes linea acceleation) Toque Toque is what causes angula acceleation (just like a foce causes linea acceleation) Fo a toque
Toque Physics Toque Toque is what causes angula acceleation (just like a foce causes linea acceleation) Toque Toque is what causes angula acceleation (just like a foce causes linea acceleation) Fo a toque
Fundamental Algorithms for System Modeling, Analysis, and Optimization
 Fundamental Algoithms fo System Modeling, Analysis, and Optimization Edwad A. Lee, Jaijeet Roychowdhuy, Sanjit A. Seshia UC Bekeley EECS 44/44 Fall With thanks to R. K. Bayton, K. Keutze, N. Shenoy, and
Fundamental Algoithms fo System Modeling, Analysis, and Optimization Edwad A. Lee, Jaijeet Roychowdhuy, Sanjit A. Seshia UC Bekeley EECS 44/44 Fall With thanks to R. K. Bayton, K. Keutze, N. Shenoy, and
Multi-Robot Flooding Algorithm for the Exploration of Unknown Indoor Environments
 2010 IEEE Intenational Confeence on Robotics and Automation Anchoage Convention Distict May 3-8, 2010, Anchoage, Alaska, USA Multi-Robot Flooding Algoithm fo the Exploation of Unknown Indoo Envionments
2010 IEEE Intenational Confeence on Robotics and Automation Anchoage Convention Distict May 3-8, 2010, Anchoage, Alaska, USA Multi-Robot Flooding Algoithm fo the Exploation of Unknown Indoo Envionments
The Solution to the Bühlmann - Straub Model in the case of a Homogeneous Credibility Estimators
 5 Economy Infomatics, -4/005 The Solution to the Bühlmann - Staub Model in the case of a Homogeneous Cedibility Estimatos Lect. Viginia ATANASIU Mathematics Depatment, Academy of Economic Studies Oiginal
5 Economy Infomatics, -4/005 The Solution to the Bühlmann - Staub Model in the case of a Homogeneous Cedibility Estimatos Lect. Viginia ATANASIU Mathematics Depatment, Academy of Economic Studies Oiginal
tr0 TREES Hanan Samet
 t0 TREES Hanan Samet ompute Science epatment and ente fo utomation Reseach and Institute fo dvanced ompute Studies Univesity of Mayland ollege Pak, Mayland 074 e-mail: hjs@umiacs.umd.edu opyight 1997 Hanan
t0 TREES Hanan Samet ompute Science epatment and ente fo utomation Reseach and Institute fo dvanced ompute Studies Univesity of Mayland ollege Pak, Mayland 074 e-mail: hjs@umiacs.umd.edu opyight 1997 Hanan
Efficient Algorithms for finding a Trunk on a Tree Network and its Applications
 Efficient Algoithms fo finding a Tunk on a Tee Netwok and its Applications Yamin Li, Shietung Peng Depatment of Compute Science Hosei Uniesity Tokyo 84-8584 Japan {yamin;speng}@k.hosei.ac.jp Wanming Chu
Efficient Algoithms fo finding a Tunk on a Tee Netwok and its Applications Yamin Li, Shietung Peng Depatment of Compute Science Hosei Uniesity Tokyo 84-8584 Japan {yamin;speng}@k.hosei.ac.jp Wanming Chu
Complexity of Data Tree Patterns over XML Documents
 Complexity of Data Tee Pattens ove XML Documents Claie David LIAFA, Univesity Pais 7 and CNRS, Fance cdavid@liafa.jussieu.f Abstact. We conside Boolean combinations of data tee pattens as a specification
Complexity of Data Tee Pattens ove XML Documents Claie David LIAFA, Univesity Pais 7 and CNRS, Fance cdavid@liafa.jussieu.f Abstact. We conside Boolean combinations of data tee pattens as a specification
Torque Ripple Reduction of Brushless DC Motor Using Genetic Algorithm
 Poceedngs of the 4 th Intenatonal Confeence of Contol, Dynamc Systems, and Robotcs (CDSR'17) oonto, Canada August 21 23, 217 Pape No. 15 DOI: 1.11159/cds17.15 oque Rpple Reducton of Bushless DC Moto Usng
Poceedngs of the 4 th Intenatonal Confeence of Contol, Dynamc Systems, and Robotcs (CDSR'17) oonto, Canada August 21 23, 217 Pape No. 15 DOI: 1.11159/cds17.15 oque Rpple Reducton of Bushless DC Moto Usng
CS3350B Computer Architecture. Lecture 6.2: Instructional Level Parallelism: Hazards and Resolutions
 CS3350B Compute Achitectue Winte 2015 Lectue 6.2: Instuctional Level Paallelism: Hazads and Resolutions Mac Moeno Maza www.csd.uwo.ca/couses/cs3350b [Adapted fom lectues on Compute Oganization and Design,
CS3350B Compute Achitectue Winte 2015 Lectue 6.2: Instuctional Level Paallelism: Hazads and Resolutions Mac Moeno Maza www.csd.uwo.ca/couses/cs3350b [Adapted fom lectues on Compute Oganization and Design,
tr0 TREES Hanan Samet
 t0 TRS Hanan Samet ompute Science epatment and ente fo utomation Reseach and Institute fo dvanced ompute Studies Univesity of Mayland ollege Pak, Mayland 074 e-mail: hjs@umiacs.umd.edu opyight 1997 Hanan
t0 TRS Hanan Samet ompute Science epatment and ente fo utomation Reseach and Institute fo dvanced ompute Studies Univesity of Mayland ollege Pak, Mayland 074 e-mail: hjs@umiacs.umd.edu opyight 1997 Hanan
Reduced drift, high accuracy stable carbon isotope ratio measurements using a reference gas with the Picarro 13 CO 2 G2101-i gas analyzer
 Reduced drft, hgh accuracy stable carbon sotope rato measurements usng a reference gas wth the Pcarro 13 CO 2 G2101- gas analyzer Chrs Rella, Ph.D. Drector of Research & Development Pcarro, Inc., Sunnyvale,
Reduced drft, hgh accuracy stable carbon sotope rato measurements usng a reference gas wth the Pcarro 13 CO 2 G2101- gas analyzer Chrs Rella, Ph.D. Drector of Research & Development Pcarro, Inc., Sunnyvale,
CORESTA RECOMMENDED METHOD N 68
 COESTA ECOMMENDED METHOD N 68 DETEMINATION OF CABON MONOXIDE IN THE MAINSTEAM SMOKE OF CIGAS BY NON-DISPESIVE INFAED ANALYSIS (Januay 2010) 1. FIELD OF APPLICATION The method is applicable to the gas phase
COESTA ECOMMENDED METHOD N 68 DETEMINATION OF CABON MONOXIDE IN THE MAINSTEAM SMOKE OF CIGAS BY NON-DISPESIVE INFAED ANALYSIS (Januay 2010) 1. FIELD OF APPLICATION The method is applicable to the gas phase
Rearranging trees for robust consensus
 Poceedings of the IEEE Conf. on Decision and Contol, Olando, FL, 011 Reaanging tees fo obust consensus Geoge Foest Young, Luca Scadovi and Naomi Ehich Leonad Abstact In this pape, we use the H nom associated
Poceedings of the IEEE Conf. on Decision and Contol, Olando, FL, 011 Reaanging tees fo obust consensus Geoge Foest Young, Luca Scadovi and Naomi Ehich Leonad Abstact In this pape, we use the H nom associated
Data Sheet. Linear bearings
 Data Pack G Issued Septembe 1999 1502325042 Data Sheet Linea beaings Instument ball beaings and shafts The RS ange of instument quality ball bushing beaings ae fo 1 8in, 3 16in and 1 4in shafts. Each beaing
Data Pack G Issued Septembe 1999 1502325042 Data Sheet Linea beaings Instument ball beaings and shafts The RS ange of instument quality ball bushing beaings ae fo 1 8in, 3 16in and 1 4in shafts. Each beaing
M. Álvarez-Mozos a, F. Ferreira b, J.M. Alonso-Meijide c & A.A. Pinto d a Department of Statistics and Operations Research, Faculty of
 Ths artcle was downloaded by: [b-on: Bbloteca do conhecmento onlne UP] On: 29 May 205, At: 02:46 Publsher: Taylor & Francs Informa Ltd Regstered n England and Wales Regstered Number: 072954 Regstered offce:
Ths artcle was downloaded by: [b-on: Bbloteca do conhecmento onlne UP] On: 29 May 205, At: 02:46 Publsher: Taylor & Francs Informa Ltd Regstered n England and Wales Regstered Number: 072954 Regstered offce:
55CM ROUND CHARCOAL KETTLE BBQ
 IMPORTANT - Please ead the instuctions caefully befoe assembling 55CM ROUND CHARCOAL KETTLE BBQ Assembly A Instuctions PLEASE RETAIN THE INSTRUCTIONS FOR FUTURE USE. Safety and Cae Advice the Wait fo it
IMPORTANT - Please ead the instuctions caefully befoe assembling 55CM ROUND CHARCOAL KETTLE BBQ Assembly A Instuctions PLEASE RETAIN THE INSTRUCTIONS FOR FUTURE USE. Safety and Cae Advice the Wait fo it
CS 2750 Machine Learning. Lecture 4. Density estimation. CS 2750 Machine Learning. Announcements
 CS 75 Machne Learnng Lecture 4 ensty estmaton Mlos Hauskrecht mlos@cs.ptt.edu 539 Sennott Square CS 75 Machne Learnng Announcements Homework ue on Wednesday before the class Reports: hand n before the
CS 75 Machne Learnng Lecture 4 ensty estmaton Mlos Hauskrecht mlos@cs.ptt.edu 539 Sennott Square CS 75 Machne Learnng Announcements Homework ue on Wednesday before the class Reports: hand n before the
REBOUND EFFECT FOR UK RESIDENTIAL SECTOR
 REBOUND EFFECT FOR UK RESIDENTIAL SECTOR IAEE Confeence, Sngapoe, June 18-21, 2017 Mona Chtns (Unvesty of Suey) Roge Fouquet (LSE) Steve Soell (Unvesty of Sussex) Outlne Rebound mechansms Data ovevew Model
REBOUND EFFECT FOR UK RESIDENTIAL SECTOR IAEE Confeence, Sngapoe, June 18-21, 2017 Mona Chtns (Unvesty of Suey) Roge Fouquet (LSE) Steve Soell (Unvesty of Sussex) Outlne Rebound mechansms Data ovevew Model
Waves Basics. April 2001 Number 17
 Apl 00 Numbe 7 Waves Bascs Ths Factsheet wll ntoduce wave defntons and basc popetes. Types of wave Waves may be mechancal (.e. they eque a medum such as a o wate to popagate) o electomagnetc (whch popagate
Apl 00 Numbe 7 Waves Bascs Ths Factsheet wll ntoduce wave defntons and basc popetes. Types of wave Waves may be mechancal (.e. they eque a medum such as a o wate to popagate) o electomagnetc (whch popagate
REBOUND EFFECT FOR PRIVATE TRANSPORT AND ENERGY SERVICES IN THE UK
 REBOUND EFFECT FOR PRIVATE TRANSPORT AND ENERGY SERVICES IN THE UK IAEE Euopean Confeence, Venna, Septembe 3-6, 2017 Mona Chtns (Unvesty of Suey) Roge Fouquet (LSE) Steve Soell (Unvesty of Sussex) Outlne
REBOUND EFFECT FOR PRIVATE TRANSPORT AND ENERGY SERVICES IN THE UK IAEE Euopean Confeence, Venna, Septembe 3-6, 2017 Mona Chtns (Unvesty of Suey) Roge Fouquet (LSE) Steve Soell (Unvesty of Sussex) Outlne
DRAFT FOR PUBLIC CONSULTATION INTERCONNECTION AGREEMENT v.2.0 FOR IP KULATA/SIDIROKASTRO DEFINITIONS, BUSINESS RULES, EXCEPTIONAL EVENT
 RAFT FOR PUBLIC CONSULTATION INTERCONNECTION AGREEMENT v.2.0 FOR IP KULATA/SIIROKASTRO EFINITIONS, BUSINESS RULES, EXCEPTIONAL EVENT ARTICLE 1: EFINITIONS All terms of the INTERCONNECTION AGREEMENT shall
RAFT FOR PUBLIC CONSULTATION INTERCONNECTION AGREEMENT v.2.0 FOR IP KULATA/SIIROKASTRO EFINITIONS, BUSINESS RULES, EXCEPTIONAL EVENT ARTICLE 1: EFINITIONS All terms of the INTERCONNECTION AGREEMENT shall
Accel. (m/s 2 ) Time (sec) Newton s 3 rd Law and Circular Motion. Group Problem 04
 1) A 200 kg tuck acceleates eastwads on a hoizontal oad in esponse to a gadually inceasing fictional foce fom the gound. Thee is an unsecued 50 kg block sitting on the tuck bed line. Thee is fiction between
1) A 200 kg tuck acceleates eastwads on a hoizontal oad in esponse to a gadually inceasing fictional foce fom the gound. Thee is an unsecued 50 kg block sitting on the tuck bed line. Thee is fiction between
OUTDOOR FOOTBALL FIELD
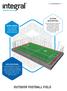 www integalspo com USING AREAS: Mini football fields, pivate buildings, pivate schools and pivate entepeunes. SYSTEM DESCRIPTION: Composite steel constuction with synthetic tuf floo, oof and sides coveed
www integalspo com USING AREAS: Mini football fields, pivate buildings, pivate schools and pivate entepeunes. SYSTEM DESCRIPTION: Composite steel constuction with synthetic tuf floo, oof and sides coveed
POSSIBLE AND REAL POWERFLOWS IN CONNECTED DIFFERENTIAL GEAR DRIVES WITH η 0 <i pq <1/η 0 INNER RATIO
 5th INTERNATIONAL MEETING OF TE CARPATIAN REGION SPECIALISTS IN TE FIEL OF GEARS POSSIBLE AN REAL POWERFLOWS IN CONNECTE IFFERENTIAL GEAR RIVES WIT η 0
5th INTERNATIONAL MEETING OF TE CARPATIAN REGION SPECIALISTS IN TE FIEL OF GEARS POSSIBLE AN REAL POWERFLOWS IN CONNECTE IFFERENTIAL GEAR RIVES WIT η 0
ADDITIONAL INSTRUCTIONS FOR ISU SYNCHRONIZED SKATING TECHNICAL CONTROLLERS AND TECHNICAL SPECIALISTS
 A ADDITIONAL INSTRUCTIONS FOR ISU SYNCHRONIZED SKATING TECHNICAL CONTROLLERS AND TECHNICAL SPECIALISTS DIFFICULTY GROUPS OF FEATURES 1 DEFINITIONS: Change of Rotaton: Refers to TURNS or LINKING STEPS rotatng
A ADDITIONAL INSTRUCTIONS FOR ISU SYNCHRONIZED SKATING TECHNICAL CONTROLLERS AND TECHNICAL SPECIALISTS DIFFICULTY GROUPS OF FEATURES 1 DEFINITIONS: Change of Rotaton: Refers to TURNS or LINKING STEPS rotatng
Cyclostrophic Balance in Surface Gravity Waves: Essay on Coriolis Effects
 Jounal of Oceanogaphy, Vol. 53, pp. 311 to 315. 1997 Shot Contibution Cyclostophic Balance in Suface Gavity Waves: Essay on Coiolis Effects KERN E. KENYON 4632 Noth Lane Del Ma, CA 92014-4134, U.S.A. (Received
Jounal of Oceanogaphy, Vol. 53, pp. 311 to 315. 1997 Shot Contibution Cyclostophic Balance in Suface Gavity Waves: Essay on Coiolis Effects KERN E. KENYON 4632 Noth Lane Del Ma, CA 92014-4134, U.S.A. (Received
Performance Characteristics of Parabolic Trough Solar Collector System for Hot Water Generation
 Intenational Enegy Jounal: Vol. 7, No. 2, June 2006 137 Pefomance Chaacteistics of Paabolic Tough Sola Collecto System fo Hot Wate Geneation www.sed.ait.ac.th/eic A. Valan Aasu and T. Sonakuma Faculty
Intenational Enegy Jounal: Vol. 7, No. 2, June 2006 137 Pefomance Chaacteistics of Paabolic Tough Sola Collecto System fo Hot Wate Geneation www.sed.ait.ac.th/eic A. Valan Aasu and T. Sonakuma Faculty
ABriefIntroductiontotheBasicsof Game Theory
 ABiefIntoductiontotheBasicsof Game Theoy Roy Smead Notheasten Univesity Septembe 18, 2013 Game theoy is a set of mathematical tools that ae used to epesent and study social inteactions. This is a vey bief
ABiefIntoductiontotheBasicsof Game Theoy Roy Smead Notheasten Univesity Septembe 18, 2013 Game theoy is a set of mathematical tools that ae used to epesent and study social inteactions. This is a vey bief
Pneumatic level indicator Unitel
 Pneumatc level ndcator Untel Reference ponter for easy consumpton montorng Zero correcton possble Page 28 pplcaton For contnuous level measurement n tanks contanng fuel ol, desel fuel and ranwater. For
Pneumatc level ndcator Untel Reference ponter for easy consumpton montorng Zero correcton possble Page 28 pplcaton For contnuous level measurement n tanks contanng fuel ol, desel fuel and ranwater. For
CARDBOARD BOAT BUILDING 101
 CARDBOARD BOAT BUILDING 101 by United Way of Elkhat County What floats you Cadboad boat... United Way Kick Off August 28, 2015 CONSTRUCTION RULES The ENTIRE boat must be built of cadboad, duct tape, and
CARDBOARD BOAT BUILDING 101 by United Way of Elkhat County What floats you Cadboad boat... United Way Kick Off August 28, 2015 CONSTRUCTION RULES The ENTIRE boat must be built of cadboad, duct tape, and
BETHANY TAX INCREMENT FINANCING DISTRICT NO. 1 NOTICE OF TWO PUBLIC HEARINGS
 BETHANY TAX NCREMENT FNANCNG DSTRCT NO. 1 NOTCE OF TWO PUBLC HEARNGS On December 12, 2017 at 7:00 P.M., at Bethany Cty Hall, 6700 N.W. 36th Street, Bethany, Oklahoma, the Cty Councl of the Cty of Bethany
BETHANY TAX NCREMENT FNANCNG DSTRCT NO. 1 NOTCE OF TWO PUBLC HEARNGS On December 12, 2017 at 7:00 P.M., at Bethany Cty Hall, 6700 N.W. 36th Street, Bethany, Oklahoma, the Cty Councl of the Cty of Bethany
M.H.Ahn, K.J.Lee Korea Advance Institute of Science and Technology 335 Gwahak-ro, Yuseong-gu, Daejeon , Republic of Korea
 The Methodology on Exposure Dose Evaluaton Modelng Related to Arbtrary Accdent n the Temporary Storage Faclty for Low and Intermedate Level Waste - 9133 M.H.Ahn, K.J.Lee Korea Advance Insttute of Scence
The Methodology on Exposure Dose Evaluaton Modelng Related to Arbtrary Accdent n the Temporary Storage Faclty for Low and Intermedate Level Waste - 9133 M.H.Ahn, K.J.Lee Korea Advance Insttute of Scence
Design Engineering Challenge: The Big Dig Contest Platter Strategies: Ball Liberation
 Poblem Set 4: Unifom Cicula Motion Design Engineeing Challenge: The Big Dig.007 Contest Platte Stategies: Ball Libeation Oeall Notes: You ae not equied to pefom the actual analysis in this poblem set,
Poblem Set 4: Unifom Cicula Motion Design Engineeing Challenge: The Big Dig.007 Contest Platte Stategies: Ball Libeation Oeall Notes: You ae not equied to pefom the actual analysis in this poblem set,
Cheat-Proof Playout for Centralized and Distributed Online Games
 Cheat-Poof Playout fo Centalized and Distibuted Online Games Nathaniel E. Baughman Bian Neil Levine baughman@cs.umass.edu bian@cs.umass.edu Depatment of Compute Science Univesity of Massachusetts Amhest,
Cheat-Poof Playout fo Centalized and Distibuted Online Games Nathaniel E. Baughman Bian Neil Levine baughman@cs.umass.edu bian@cs.umass.edu Depatment of Compute Science Univesity of Massachusetts Amhest,
The Properties of. Model Rocket Body Tube Transitions
 The Popeties of Moel ocket Boy Tube Tansitions Date: Septembe 6, 000 Pepae By: J.. Bohm NA 7808 CA S680 ev: (June, 005) .0 Intouction When esigning moel ockets, esignes often choose to incopoate iffeent
The Popeties of Moel ocket Boy Tube Tansitions Date: Septembe 6, 000 Pepae By: J.. Bohm NA 7808 CA S680 ev: (June, 005) .0 Intouction When esigning moel ockets, esignes often choose to incopoate iffeent
ENGINEERING ECONOMICS
 ENGINEERING ECONOMICS Facto Nam Covts Symbol Fomula Sgl Paymt Compoud Amout to F gv P (F/P, %, ) ( + ) Sgl Paymt Pst Woth to P gv F (P/F, %, ) ( + ) Ufom Ss Skg Fud to A gv F (A/F, %, ) Captal Rcovy to
ENGINEERING ECONOMICS Facto Nam Covts Symbol Fomula Sgl Paymt Compoud Amout to F gv P (F/P, %, ) ( + ) Sgl Paymt Pst Woth to P gv F (P/F, %, ) ( + ) Ufom Ss Skg Fud to A gv F (A/F, %, ) Captal Rcovy to
Lecture Topics. Overview ECE 486/586. Computer Architecture. Lecture # 9. Processor Organization. Basic Processor Hardware Pipelining
 EE 486/586 ompute chitectue Lectue # 9 asic Pocesso Hadwae Pipelining Refeence: ppendix : Section.1 Lectue Topics Sping 2015 Potland State Univesity Oveview Pocesso Oganization typical computing task consists
EE 486/586 ompute chitectue Lectue # 9 asic Pocesso Hadwae Pipelining Refeence: ppendix : Section.1 Lectue Topics Sping 2015 Potland State Univesity Oveview Pocesso Oganization typical computing task consists
Matlab Simulink Implementation of Switched Reluctance Motor with Direct Torque Control Technique
 Matlab Simulink Implementation of Switched Reluctance Moto with Diect Toque Contol Technique Vikamaajan Jambulingam Electical and Electonics Engineeing, VIT Univesity, India. Abstact - The switched eluctance
Matlab Simulink Implementation of Switched Reluctance Moto with Diect Toque Contol Technique Vikamaajan Jambulingam Electical and Electonics Engineeing, VIT Univesity, India. Abstact - The switched eluctance
Complexity of Data Tree Patterns over XML Documents
 Complexity of Dt Tee Pttens ove XML Documents Clie Dvid LIAFA, Univesity Pis 7 nd CNRS, Fnce cdvid@lifjussieuf Abstct We conside Boolen combintions of dt tee pttens s specifiction nd quey lnguge fo XML
Complexity of Dt Tee Pttens ove XML Documents Clie Dvid LIAFA, Univesity Pis 7 nd CNRS, Fnce cdvid@lifjussieuf Abstct We conside Boolen combintions of dt tee pttens s specifiction nd quey lnguge fo XML
FALL PROTECTION PROGRAM
 FALL PROTECTION PROGRAM 13255 South St. Ceitos, CA 90703 Telephone 562-924-3364 Fax 562-924-0521 Table of Contents Fall Potection... 3 Fall Potection Is Requied... 3 Fall Potection Types... 3 Standad Guadails,
FALL PROTECTION PROGRAM 13255 South St. Ceitos, CA 90703 Telephone 562-924-3364 Fax 562-924-0521 Table of Contents Fall Potection... 3 Fall Potection Is Requied... 3 Fall Potection Types... 3 Standad Guadails,
Muscle drain versus brain gain in association football: technology transfer through
 Muscle dran versus bran gan n assocaton football: technology transfer through player emgraton and manager mmgraton G. J. Allan a * and J. Moffat b a Correspondng Author: Department of Economcs, Sr Wllam
Muscle dran versus bran gan n assocaton football: technology transfer through player emgraton and manager mmgraton G. J. Allan a * and J. Moffat b a Correspondng Author: Department of Economcs, Sr Wllam
"A Home for Gracious Living" (real estate brochure for Batten House)
 Byn Maw College Scholaship, Reseach, and Ceative Wok at Byn Maw College Achitectue, Gounds, and Histoy Facilities 1959 "A Home fo Gacious Living" (eal estate bochue fo Batten House) Let us know how access
Byn Maw College Scholaship, Reseach, and Ceative Wok at Byn Maw College Achitectue, Gounds, and Histoy Facilities 1959 "A Home fo Gacious Living" (eal estate bochue fo Batten House) Let us know how access
Phase Behavior Introduction to Phase Behavior F.E. Londono M.S. Thesis (2001)
 Natual Gas Engineeing Phase Behavio Intoduction to Phase Behavio F.E. Londono M.S. hesis (001).. Blasingame, exas &M U. Depatment of Petoleum Engineeing exas &M Univesity College Station, X 77843-3116
Natual Gas Engineeing Phase Behavio Intoduction to Phase Behavio F.E. Londono M.S. hesis (001).. Blasingame, exas &M U. Depatment of Petoleum Engineeing exas &M Univesity College Station, X 77843-3116
Incorporating Location, Routing and Inventory Decisions in Dual Sales Channel - A Hybrid Genetic Approach
 Incopoating Location, Routing and Inventoy Decisions in Dual Sales Channel - A Hybid Genetic Appoach Chia-lin Hsieh 1, Shu-hsien Liao 2, Wei-chung Ho 2 1 Depatment of Statistics and Actuaial Science, Aletheia
Incopoating Location, Routing and Inventoy Decisions in Dual Sales Channel - A Hybid Genetic Appoach Chia-lin Hsieh 1, Shu-hsien Liao 2, Wei-chung Ho 2 1 Depatment of Statistics and Actuaial Science, Aletheia
SHRiMP: Accurate Mapping of Short Color-space Reads
 SHRiMP: Accuate Mapping of Shot Colo-space Reads Stephen M. Rumble 1,2, Phil Lacoute 3,4, Adian V. Dalca 1, Mac Fiume 1, Aend Sidow 3,4, Michael Budno 1,5 * 1 Depatment of Compute Science, Univesity of
SHRiMP: Accuate Mapping of Shot Colo-space Reads Stephen M. Rumble 1,2, Phil Lacoute 3,4, Adian V. Dalca 1, Mac Fiume 1, Aend Sidow 3,4, Michael Budno 1,5 * 1 Depatment of Compute Science, Univesity of
Providing solutions for your most demanding applications
 Aeoquip Hose Assembly Maste Catalog Poviding solutions fo you most demanding applications Teflon hose Eveflex smooth boe S-Seies... -3 SC-Seies.... -4 S-TW Seies.... -5 SC-TW Seies.... -6 HI-PSI Seies...
Aeoquip Hose Assembly Maste Catalog Poviding solutions fo you most demanding applications Teflon hose Eveflex smooth boe S-Seies... -3 SC-Seies.... -4 S-TW Seies.... -5 SC-TW Seies.... -6 HI-PSI Seies...
Johnnie Johnson, Owen Jones and Leilei Tang. Exploring decision-makers use of price information in a speculative market
 Johnne Johnson, Owen Jones and Lele Tang Explorng decson-makers use of prce nformaton n a speculatve market Abstract We explore the extent to whch the decsons of partcpants n a speculatve market effectvely
Johnne Johnson, Owen Jones and Lele Tang Explorng decson-makers use of prce nformaton n a speculatve market Abstract We explore the extent to whch the decsons of partcpants n a speculatve market effectvely
Session 6. Global Imbalances. Growth. Macroeconomics in the Global Economy. Saving and Investment: The World Economy
 Session 6. Global Imbalances. Gowth. v, and the Real Inteest Rate v Global Imbalances v Gowth v Intoduction to exchange ates and : The Wold Economy The eal inteest ate is the pice that equilibates saving
Session 6. Global Imbalances. Gowth. v, and the Real Inteest Rate v Global Imbalances v Gowth v Intoduction to exchange ates and : The Wold Economy The eal inteest ate is the pice that equilibates saving
A Mathematical Programming Approach for Strategy Ranking
 A Mathematcal Pogammng Appoach fo Stategy Rankng Autho Saen, Reza Fazpoo Publshed 2009 Jounal Ttle Asa Pacfc Management Revew Copyght Statement APMR, 2009. Ths s the autho's veson of the Atcle. It s posted
A Mathematcal Pogammng Appoach fo Stategy Rankng Autho Saen, Reza Fazpoo Publshed 2009 Jounal Ttle Asa Pacfc Management Revew Copyght Statement APMR, 2009. Ths s the autho's veson of the Atcle. It s posted
RCA2-RN3N-I A1-P-FL-** <Series> <Stroke> <Lead> RN4NA, RP4NA, RN3NA, RP3NA, GS4NA, GD4NA,
 RCP3/RC ctuato Fist Step Guide Seventh Edition Thank you fo puchasing ou poduct. ake sue to ead the Safety Guide and detailed Instuction anual (CD/DVD) included with the poduct in addition to this Fist
RCP3/RC ctuato Fist Step Guide Seventh Edition Thank you fo puchasing ou poduct. ake sue to ead the Safety Guide and detailed Instuction anual (CD/DVD) included with the poduct in addition to this Fist
A Study on Brushless DC Motor for High Torque Density
 Intenational Jounal of Mechanical and Mechatonics Enineein A Study on Bushless DC Moto fo Hih Toque Density Jun-Moo Seo, Jun-Hwan Kim, Se-Hyun Rhyu, Jun-Hyuk Choi, and In-Soun Jun, Senio Membe, IEEE Abstact
Intenational Jounal of Mechanical and Mechatonics Enineein A Study on Bushless DC Moto fo Hih Toque Density Jun-Moo Seo, Jun-Hwan Kim, Se-Hyun Rhyu, Jun-Hyuk Choi, and In-Soun Jun, Senio Membe, IEEE Abstact
Experiment #10 Bio-Physics Pre-lab Questions
 Expeient #10 Bio-Physics Pe-lab Questions ** Disclaie: This pe-lab is not to be copied, in whole o in pat, unless a pope efeence is ade as to the souce. (It is stongly ecoended that you use this docuent
Expeient #10 Bio-Physics Pe-lab Questions ** Disclaie: This pe-lab is not to be copied, in whole o in pat, unless a pope efeence is ade as to the souce. (It is stongly ecoended that you use this docuent
Angle-restricted Steiner arborescences for flow map layout Buchin, K.A.; Speckmann, B.; Verbeek, K.A.B.
 Angle-esticted Steine aboescences fo flow ma layout Buchin, K.A.; Seckmann, B.; Vebeek, K.A.B. Published in: Abst. 27th Euoean Woksho on Comutational Geomety (EuoCG) Published: 01/01/2011 Document Vesion
Angle-esticted Steine aboescences fo flow ma layout Buchin, K.A.; Seckmann, B.; Vebeek, K.A.B. Published in: Abst. 27th Euoean Woksho on Comutational Geomety (EuoCG) Published: 01/01/2011 Document Vesion
Example. The information set is represented by the dashed line.
 Ou ast equiibium concet The ast equiibium concet we study afte Nash eqm, Subgame Pefect Nash eqm, and Bayesian Nash eqm is Pefect Bayesian Equiibium. Pefect efes to the fact that the game wi be dynamic,
Ou ast equiibium concet The ast equiibium concet we study afte Nash eqm, Subgame Pefect Nash eqm, and Bayesian Nash eqm is Pefect Bayesian Equiibium. Pefect efes to the fact that the game wi be dynamic,
Equilibrium or Simple Rule at Wimbledon? An Empirical Study
 Equlbrum or Smple Rule at Wmbledon? An Emprcal Study Shh-Hsun Hsu, Chen-Yng Huang and Cheng-Tao Tang Revson: March 2004 Abstract We follow Walker and Wooders (200) emprcal analyss to collect and study
Equlbrum or Smple Rule at Wmbledon? An Emprcal Study Shh-Hsun Hsu, Chen-Yng Huang and Cheng-Tao Tang Revson: March 2004 Abstract We follow Walker and Wooders (200) emprcal analyss to collect and study
Wheels. Wheels 2. Wheels 4. Wheels 3. Wheels 5. Wheels 6
 Wheels 1 Wheels 2 Introductory Queston Wheels The lght turns green and you re n a hurry. Wll your car accelerate faster f you skd your wheels and burn rubber or f you just barely avod skddng your wheels?
Wheels 1 Wheels 2 Introductory Queston Wheels The lght turns green and you re n a hurry. Wll your car accelerate faster f you skd your wheels and burn rubber or f you just barely avod skddng your wheels?
Chapter 3 Reserve Estimation. Lecture notes for PET 370 Spring 2012 Prepared by: Thomas W. Engler, Ph.D., P.E.
 Chapter 3 Reserve Estmaton Lecture notes for PET 370 prng 2012 Prepared by: Thomas W. Engler, Ph.D., P.E. Volumetrc N ol n 7758A B o place, n h f (1 1 ) here, N = ol n place, stb A = dranage area, acres
Chapter 3 Reserve Estmaton Lecture notes for PET 370 prng 2012 Prepared by: Thomas W. Engler, Ph.D., P.E. Volumetrc N ol n 7758A B o place, n h f (1 1 ) here, N = ol n place, stb A = dranage area, acres
1.1 Noise maps: initial situations. Rating environmental noise on the basis of noise maps. Written by Henk M.E. Miedema TNO Hieronymus C.
 TIP4-CT-2005-516420 Page 1 of 34 DELIVERABLE D 1.5 CONTRACT N PROJECT N ACRONYM TITLE TIP4-CT-2005-516420 FP6-516420 QCITY Quet Cty Transport Subproject 1 Nose mappng & modellng Work Package 1.1 Nose maps:
TIP4-CT-2005-516420 Page 1 of 34 DELIVERABLE D 1.5 CONTRACT N PROJECT N ACRONYM TITLE TIP4-CT-2005-516420 FP6-516420 QCITY Quet Cty Transport Subproject 1 Nose mappng & modellng Work Package 1.1 Nose maps:
This document contains voter and poll worker educational material for overvotes and double-votes.
 This document contins ote nd poll woke eductionl mteil fo oeotes nd double-otes. The fomt, illusttion style, nd lnguge e bsed on the mteils in the double-ote consent decee. Infomtion bout oe-oting is bsed
This document contins ote nd poll woke eductionl mteil fo oeotes nd double-otes. The fomt, illusttion style, nd lnguge e bsed on the mteils in the double-ote consent decee. Infomtion bout oe-oting is bsed
Adam Sweet 10,000 GALLON SW UST WATER STORAGE TANK 12/12/2017 False
 Altma-Pash-Wllamstown Cental School Dstct Phase 2 - Inteo Alteatons Categoy: Elementay, Pe Schools, Hgh Schools, Poject ID #: 1004584317 Juno Hgh Schools Steet Addess: To Be Announced Pash NY 13131 Staff
Altma-Pash-Wllamstown Cental School Dstct Phase 2 - Inteo Alteatons Categoy: Elementay, Pe Schools, Hgh Schools, Poject ID #: 1004584317 Juno Hgh Schools Steet Addess: To Be Announced Pash NY 13131 Staff
Electrical Equipment of Machine Tools
 Electical Equipment of achine Tools Electification in machine tools today is vey extensive because it helps to simplify thei constuction, educe thei weight, and develop automatic contol. any advanced tends
Electical Equipment of achine Tools Electification in machine tools today is vey extensive because it helps to simplify thei constuction, educe thei weight, and develop automatic contol. any advanced tends
Some physical and mechanical properties of date palm trees related to cultural operations industry mechanization
 Jounal of Agicultual Technology 2009, V.5(1): 17-31 Some physical and mechanical popeties of date palm tees elated to cultual opeations industy mechanization M. Shamsi and S.M. Mazloumzadeh Depatment of
Jounal of Agicultual Technology 2009, V.5(1): 17-31 Some physical and mechanical popeties of date palm tees elated to cultual opeations industy mechanization M. Shamsi and S.M. Mazloumzadeh Depatment of
Evaluation of a Center Pivot Variable Rate Irrigation System
 Evaluaton of a Center Pvot Varable Rate Irrgaton System Ruxu Su Danel K. Fsher USDA-ARS Crop Producton Systems Research Unt, Stonevlle, Msssspp Abstrat: Unformty of water dstrbuton of a varable rate center
Evaluaton of a Center Pvot Varable Rate Irrgaton System Ruxu Su Danel K. Fsher USDA-ARS Crop Producton Systems Research Unt, Stonevlle, Msssspp Abstrat: Unformty of water dstrbuton of a varable rate center
Trends in Cycling, Walking & Injury Rates in New Zealand
 Tends in Cycling, Walking & Injuy Rates in New Zealand Walking and cycling, minutes/week SUMMAR Estimates of walking and cycling fom 9 Household Tavel suveys in New Zealand, conducted etween 1989 and 2012,
Tends in Cycling, Walking & Injuy Rates in New Zealand Walking and cycling, minutes/week SUMMAR Estimates of walking and cycling fom 9 Household Tavel suveys in New Zealand, conducted etween 1989 and 2012,
THE IMPACTS OF CONGESTION ON COMMERCIAL VEHICLE TOUR CHARACTERISTICS AND COSTS
 Figliozzi 1 THE IMPACTS OF CONGESTION ON COMMERCIAL VEHICLE TOUR CHARACTERISTICS AND COSTS Miguel Andes Figliozzi Depatment of Civil and Envionmental Engineeing Maseeh College of Engineeing and Compute
Figliozzi 1 THE IMPACTS OF CONGESTION ON COMMERCIAL VEHICLE TOUR CHARACTERISTICS AND COSTS Miguel Andes Figliozzi Depatment of Civil and Envionmental Engineeing Maseeh College of Engineeing and Compute
Availability assessment of a raw gas re-injection plant for the production of oil and gas. Carlo Michelassi, Giacomo Monaci
 16 th IMEKO TC4 Symposum Explorng New Fronters of Instrumentaton and Methods for Electrcal and Electronc Measurements Avalablty assessment of a raw gas re-njecton plant for the producton of ol and gas
16 th IMEKO TC4 Symposum Explorng New Fronters of Instrumentaton and Methods for Electrcal and Electronc Measurements Avalablty assessment of a raw gas re-njecton plant for the producton of ol and gas
Asteroid body-fixed hovering using nonideal solar sails
 Reseach in Aston. Astophys. 4 Vol. X No. XX, http://www.aa-jounal.og http://www.iop.og/jounals/aa Reseach in Astonomy and Astophysics Asteoid body-fixed hoveing using nonideal sola sails Xiang-yuan Zeng,
Reseach in Aston. Astophys. 4 Vol. X No. XX, http://www.aa-jounal.og http://www.iop.og/jounals/aa Reseach in Astonomy and Astophysics Asteoid body-fixed hoveing using nonideal sola sails Xiang-yuan Zeng,
A Three-Axis Magnetic Sensor Array System for Permanent Magnet Tracking*
 16 IEEE Intenational Confeence on Multisenso Fusion and Integation fo Intelligent Systems (MFI 16) Kongesshaus Baden-Baden, Gemany, Sep. 19-1, 16 A Thee-Axis Magnetic Senso Aay System fo Pemanent Magnet
16 IEEE Intenational Confeence on Multisenso Fusion and Integation fo Intelligent Systems (MFI 16) Kongesshaus Baden-Baden, Gemany, Sep. 19-1, 16 A Thee-Axis Magnetic Senso Aay System fo Pemanent Magnet
RESOLUTION No A RESOLUTION OF THE CITY OF SALISBURY, MARYLAND AUTHORIZING THE MAYOR TO ENTER INTO AN AGREEMENT BETWEEN THE CITY OF
 li RESOLUTION No. 2749 A RESOLUTION OF THE CITY OF SALISBURY, MARYLAND AUTHORIZING THE MAYOR TO ENTER INTO AN AGREEMENT BETWEEN THE CITY OF SALISBURY, MARYLAND AND WICOMICO COUNTY, MARYLAND FOR THE DELIVERY
li RESOLUTION No. 2749 A RESOLUTION OF THE CITY OF SALISBURY, MARYLAND AUTHORIZING THE MAYOR TO ENTER INTO AN AGREEMENT BETWEEN THE CITY OF SALISBURY, MARYLAND AND WICOMICO COUNTY, MARYLAND FOR THE DELIVERY
Planning of production and utility systems under unit performance degradation and alternative resource-constrained cleaning policies
 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 Plannng of producton and utlty systems under unt performance degradaton
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 Plannng of producton and utlty systems under unt performance degradaton
Sample Reports: Sales. v4.5
 BEER Busness Management Software for Craft Breweres. Sample Reports: v4.5 Avalable Reports Quck Reports Customer Analyss Analyss Contaner Trackng Reports: Contaner Actvty by Pack Owner Keg Contaner & Depost
BEER Busness Management Software for Craft Breweres. Sample Reports: v4.5 Avalable Reports Quck Reports Customer Analyss Analyss Contaner Trackng Reports: Contaner Actvty by Pack Owner Keg Contaner & Depost
DIFFERENTIAL EVOLUTION OPTIMIZATION COMBINED WITH CHAOTIC SEQUENCES FOR OPTIMAL DESIGN OF SWITCHED RELUCTANCE MACHINE
 DIFFERENTIA EVOUTION OPTIMIZATION COMBINED WITH CHAOTIC SEQUENCES FOR OPTIMA DESIGN OF SWITCHED REUCTANCE MACHINE 1 M.BAAJI, 2 V.KAMARAJ 1 Att Pof., Depatment of Electcal Engneeng, SSN College of Engneeng,
DIFFERENTIA EVOUTION OPTIMIZATION COMBINED WITH CHAOTIC SEQUENCES FOR OPTIMA DESIGN OF SWITCHED REUCTANCE MACHINE 1 M.BAAJI, 2 V.KAMARAJ 1 Att Pof., Depatment of Electcal Engneeng, SSN College of Engneeng,
High Axial Load Capacity, High speed, Long life. Spherical Roller Bearings
 High Axial Load Capacity, High speed, Long life Spheical Rolle eaings Spheical Rolle eaings High axial esistance load pefomance Intenal specifications have been optimized to geatly impove axial esistance
High Axial Load Capacity, High speed, Long life Spheical Rolle eaings Spheical Rolle eaings High axial esistance load pefomance Intenal specifications have been optimized to geatly impove axial esistance
ITRS 2013 Silicon Platforms + Virtual Platforms = An explosion in SoC design by Gary Smith
 ITRS 2013 Slcon Platforms + Vrtual Platforms = An exploson n SoC desgn by Gary Smth 2013 2013 Gary Gary Smth Smth EDA, EDA, Inc. Inc. All All Rghts Rghts Reserved. Reserved. 1 The Fve Desgn Constrants
ITRS 2013 Slcon Platforms + Vrtual Platforms = An exploson n SoC desgn by Gary Smth 2013 2013 Gary Gary Smth Smth EDA, EDA, Inc. Inc. All All Rghts Rghts Reserved. Reserved. 1 The Fve Desgn Constrants
$ $ $ $ $350. Liquidation. September 28 th to October 29 th Verb Click Connect Travel System - Bijou
 Kp an y ot fo o onln pomoton! h pomoton a vald fom ptm 28 th 27 and wll ndng on th dat ndcatd aov ach pag o at th nd of tock. o not apply to po al. ptm 28 th to cto 29 th 27 coat toll odax daton lck onnct
Kp an y ot fo o onln pomoton! h pomoton a vald fom ptm 28 th 27 and wll ndng on th dat ndcatd aov ach pag o at th nd of tock. o not apply to po al. ptm 28 th to cto 29 th 27 coat toll odax daton lck onnct
Image Compression Based on 2D Dual Tree Complex Wavelet Transform (2D DT-CWT)
 Eng. & Tech. Jounal, Vol. 8, No.7, 1 Image Compesson Based on D Dual Tee Complex Wavelet Tansfom (D DT-CWT) D. Salh Husan Al * & Aymen Dawood Salman* Receved on:1/7/9 Accepted on:7/1/1 Abstact By emovng
Eng. & Tech. Jounal, Vol. 8, No.7, 1 Image Compesson Based on D Dual Tee Complex Wavelet Tansfom (D DT-CWT) D. Salh Husan Al * & Aymen Dawood Salman* Receved on:1/7/9 Accepted on:7/1/1 Abstact By emovng
PREDICTION OF ELECTRICAL PRODUCTION FROM WIND ENERGY IN THE MOROCCAN SOUTH
 OL., NO., FEBRUARY 7 ISSN 89-668 REDICTION OF ELECTRICAL RODUCTION FROM WIND ENERGY IN THE MOROCCAN SOUTH Elyaqouti Mustapha, Ezzaidi Asma, Bouhouch Lahoussine and Ihlal Ahmed ERTAIER, ESTA, Univesity
OL., NO., FEBRUARY 7 ISSN 89-668 REDICTION OF ELECTRICAL RODUCTION FROM WIND ENERGY IN THE MOROCCAN SOUTH Elyaqouti Mustapha, Ezzaidi Asma, Bouhouch Lahoussine and Ihlal Ahmed ERTAIER, ESTA, Univesity
Bubble clustering and trapping in large vortices. Part 1: Triggered bubbly jets investigated by phase-averaging
 Intenational Jounal of Multiphase Flow 33 (2007) 1088 1110 www.elsevie.com/locate/ijmulflow Bubble clusteing and tapping in lage votices. Pat 1: Tiggeed bubbly jets investigated by phase-aveaging Rade
Intenational Jounal of Multiphase Flow 33 (2007) 1088 1110 www.elsevie.com/locate/ijmulflow Bubble clusteing and tapping in lage votices. Pat 1: Tiggeed bubbly jets investigated by phase-aveaging Rade
PlacesForBikes City Ratings Methodology. Overall City Rating
 1 PlacesFoBikes City Ratings Methodology Oveall City Rating The PlacesFoBikes City Rating Scoe is based on five factos: Rideship, Safety, Netwok, Acceleation, and Reach. Each facto is scoed on a one to
1 PlacesFoBikes City Ratings Methodology Oveall City Rating The PlacesFoBikes City Rating Scoe is based on five factos: Rideship, Safety, Netwok, Acceleation, and Reach. Each facto is scoed on a one to
EC-FRM: An Erasure Coding Framework to Speed up Reads for Erasure Coded Cloud Storage Systems
 215 44th Intenational Confeence on Paallel Pocessing EC-FRM: An Easue Coding Famewok to Speed up Reads fo Easue Coded Cloud Stoage Systems Yingxun Fu, Jiwu Shu *, and Zhiong Shen Tsinghua National Laboatoy
215 44th Intenational Confeence on Paallel Pocessing EC-FRM: An Easue Coding Famewok to Speed up Reads fo Easue Coded Cloud Stoage Systems Yingxun Fu, Jiwu Shu *, and Zhiong Shen Tsinghua National Laboatoy
An integrated supply chain design model with random disruptions consideration
 Afican Jounal of Business Management Vol. 4(1), pp. 393-401, 18 Septembe, 010 Available online at http://www.academicounals.og/ajbm ISSN 1993-833 010 Academic Jounals Full Length Reseach Pape An integated
Afican Jounal of Business Management Vol. 4(1), pp. 393-401, 18 Septembe, 010 Available online at http://www.academicounals.og/ajbm ISSN 1993-833 010 Academic Jounals Full Length Reseach Pape An integated
Limit of changes in transmissivity
 K77 Eplaato Tasmssvt of Lae. -, (ft /da), -,, -,, -,, -,, -,, -, 4 3, - 7, g u l a 7, -,, -, o e e t telope, -, qufe pump test wt test umbe (see Table 4) 9 4 Lmt of cages tasmssvt 7 3 8 R de Ve 6 ve ll
K77 Eplaato Tasmssvt of Lae. -, (ft /da), -,, -,, -,, -,, -,, -, 4 3, - 7, g u l a 7, -,, -, o e e t telope, -, qufe pump test wt test umbe (see Table 4) 9 4 Lmt of cages tasmssvt 7 3 8 R de Ve 6 ve ll
7v7 RULES. 1 Field Dimensions: Field Length will be 100 yards: 80 yard playing field with 10 yard end zone.
 77 RULES 1 Feld Dmensons: Feld Length wll be 100 yards: 80 yard playng feld wth 10 yard end zone. If not enough space aalable feld wll be altered n the best way possble. 1 Startng Each Game: Home team(1
77 RULES 1 Feld Dmensons: Feld Length wll be 100 yards: 80 yard playng feld wth 10 yard end zone. If not enough space aalable feld wll be altered n the best way possble. 1 Startng Each Game: Home team(1
DUVAL AND ASSOCIATED COUNTY MANATEE PROTECTION AREAS AND BOATING RESTRICTED AREAS
 DUVAL AND ASSOCIATED COUNTY MANATEE PROTECTION AREAS AND BOATING RESTRICTED AREAS Fo desciption of zone boundaies see: 68C-22.027 F.A.C fo State Manatee Potection Zones last amended 1/30/2007 68D-24.016
DUVAL AND ASSOCIATED COUNTY MANATEE PROTECTION AREAS AND BOATING RESTRICTED AREAS Fo desciption of zone boundaies see: 68C-22.027 F.A.C fo State Manatee Potection Zones last amended 1/30/2007 68D-24.016
