13.7 Quadratic Equations and Problem Solving
|
|
|
- Hubert Page
- 6 years ago
- Views:
Transcription
1 13.7 Quadratic Equations and Problem Solving Learning Objectives: A. Solve problems that can be modeled by quadratic equations. Key Vocabulary: Pythagorean Theorem, right triangle, hypotenuse, leg, sum, difference, product, times, twice, more than, less than, square of, consecutive odd, consecutive even Consecutive Numbers 1. Consecutive Number. Consecutive Odd Number 3. Consecutive Even Number 1 st number 1 st number 1 st number nd number + 1 nd number + nd number + 3 rd number + 3 rd number rd number th number th number th number + 6 Pythagorean Theorem In any right triangle Leg a Hypotenuse c a + b = c Leg b Class notes: Eample 1. Find two consecutive odd integers whose product is 3 more than their sum.
2 Eample. The length of a rectangular garden is 5 feet more than its width. The area of the garden is 176 square feet. Find the length and the width. Eample 3. The hypotenuse of a right triangle is 6 inches more than the shorter leg. The longer leg is 3 inches more than the shorter leg. Find the lengths of all three sides.
3 13.7 Eercises Solve. 1. A rectangle has an area of 4 square inches. The width is represented by 3 and the length is +. Find the dimensions.. The length of a rectangle is 3 cm more than the width. The area is 70 cm. Find the dimensions of the rectangle. 3. The length of a proposed rectangular flower garden is 6 m more that its width. The area of the garden is 7 m. Find the dimensions of the proposed flower garden. 4. A square field had 5 m added to its length and m added to its width. The field then had an area of 130 m. Find the length of a side of the original field. 5. A rock is dropped from a 784 foot cliff. The height h of the rock after t seconds is given by the equation h = 16t How long will it take the ball to hit the ground? 6. One leg of a right triangle measures 6 m while the length of the other leg measures meters. The hypotenuse measures ( 6) m. Find the length of all three sides. 7. The longer leg of a right triangle measures two feet more than twice the length of the shorter leg. The hypotenuse measures 3 feet more than twice the shorter leg. Find the length of all three sides. 8. Find the length of a ladder leaning against a building if the top of the ladder touches the building at a height of 1 feet. Also, the length of the ladder is 4 feet more than its distance from the base of the building. 9. One leg of a right triangle is 14 inches longer than the other leg. The hypotenuse is 6 inches long. Find the length of each leg. 10. Eight more than the square of a number is the same as si times the number. Find the number. 11. Fifteen less than the square of a number is the same as twice the number. Find the numbers. 1. Seven less than 4 times the square of a number is 18. Find the number. 13. Find two consecutive positive odd integers whose product is The sum of the squares of two consecutive integers is 41. Find the integers. 15. Find two consecutive odd integers such that the square of the first added to 3 times the second is 4.
4 16. The square of a number minus twice the number is 63. Find the number. 17. The length of a rectangular garden is 5 feet more than its width. The area of the garden is 176 square feet. Find the length and the width. 18 A student dropped a ball from the top of a 64 foot building. The height of the ball after t seconds is given by the quadratic equation h = 16t How long will it take the ball to hit the ground? 19. The length of one leg of a right triangle is 7 meters less than the length of the other leg. The length of the hypotenuse is 13 m. Find the lengths of the legs. 0. The numerical difference between the area and the circumference of a circle is 8π. Find the radius of the circle. (Hint: first factor out π in your equation.)
5 Some challenging problems: Factor: y 7 y 17. Factor: 3. A bo is made from a rectangular piece of metal with length 0 inches and width 10 inches by cutting out square corners of length and folding up the sides. a. What are the limitations of the size of? Eplain. b. Write a polynomial that gives the volume of the bo. c. Factor out the greatest common factor for this epression you found in part (b). d. Find the volume of the bo when = 3 inches. e. Write a polynomial that gives the outside surface area of the bo. (Hint: consider the size of the metal sheet and how much was cut out.) f. Factor out the greatest common factor for the epression you found in part (e). g. If the outside surface area of the bo is 184 square inches, find.
6 4. Cut the squares apart. Match equivalent epressions. You should get a new 4 4 square.
Math 154 Chapter 7.7: Applications of Quadratic Equations Objectives:
Math 154 Chapter 7.7: Applications of Quadratic Equations Objectives: Products of numbers Areas of rectangles Falling objects Cost/Profit formulas Products of Numbers Finding legs of right triangles Finding
Lesson 3: Using the Pythagorean Theorem. The Pythagorean Theorem only applies to triangles. The Pythagorean Theorem + = Example 1
Lesson 3: Using the Pythagorean Theorem The Pythagorean Theorem only applies to triangles. The Pythagorean Theorem + = Example 1 A sailboat leaves dock and travels 6 mi due east. Then it turns 90 degrees
CCM8 Unit 7: Pythagorean Theorem Vocabulary
CCM8 Unit 7: Pythagorean Theorem Vocabulary Base Exponent Hypotenuse Legs Perfect Square Pythagorean Theorem When a number is raised to a power, the number that is used as a factor The number that indicates
Name Date PD. Pythagorean Theorem
Name Date PD Pythagorean Theorem Vocabulary: Hypotenuse the side across from the right angle, it will be the longest side Legs are the sides adjacent to the right angle His theorem states: a b c In any
11.4 Apply the Pythagorean
11.4 Apply the Pythagorean Theorem and its Converse Goal p and its converse. Your Notes VOCABULARY Hypotenuse Legs of a right triangle Pythagorean theorem THE PYTHAGOREAN THEOREM Words If a triangle is
Algebra I: Strand 3. Quadratic and Nonlinear Functions; Topic 1. Pythagorean Theorem; Task 3.1.2
Algebra I: Strand 3. Quadratic and Nonlinear Functions; Topic. Pythagorean Theorem; Task 3.. TASK 3..: 30-60 RIGHT TRIANGLES Solutions. Shown here is a 30-60 right triangle that has one leg of length and
77.1 Apply the Pythagorean Theorem
Right Triangles and Trigonometry 77.1 Apply the Pythagorean Theorem 7.2 Use the Converse of the Pythagorean Theorem 7.3 Use Similar Right Triangles 7.4 Special Right Triangles 7.5 Apply the Tangent Ratio
CH 34 MORE PYTHAGOREAN THEOREM AND RECTANGLES
CH 34 MORE PYTHAGOREAN THEOREM AND RECTANGLES 317 Recalling The Pythagorean Theorem a 2 + b 2 = c 2 a c 90 b The 90 angle is called the right angle of the right triangle. The other two angles of the right
Average Speed and Average Velocity Practice
Average Speed and Average Velocity Practice Problem #1: What is the average speed of my bunny rabbit when she hops 6 meters to the east across the room in 11 seconds? Express your answer using the proper
Application of Geometric Mean
Section 8-1: Geometric Means SOL: None Objective: Find the geometric mean between two numbers Solve problems involving relationships between parts of a right triangle and the altitude to its hypotenuse
Skills Practice Skills Practice for Lesson 3.1
Skills Practice Skills Practice for Lesson.1 Name Date Get Radical or (Be) 2! Radicals and the Pythagorean Theorem Vocabulary Write the term that best completes each statement. 1. An expression that includes
Assignment. Get Radical or (Be) 2! Radicals and the Pythagorean Theorem. Simplify the radical expression. 45x 3 y 7. 28x x 2 x 2 x 2x 2 7x
Assignment Assignment for Lesson.1 Name Date Get Radical or (Be)! Radicals and the Pythagorean Theorem Simplify the radical expression. 1. 60. 60 4 15 15. 8x 5 4. 8x 5 4 7 x x x x 7x 108 108 6 6 45x y
Date: Period: Directions: Answer the following questions completely on a separate sheet of paper.
Name: Right Triangle Review Sheet Date: Period: Geometry Honors Directions: Answer the following questions completely on a separate sheet of paper. Part One: Simplify the following radicals. 1) 2) 3) 4)
Put in simplest radical form. (No decimals)
Put in simplest radical form. (No decimals) 1. 2. 3. 4. 5. 6. 5 7. 4 8. 6 9. 5 10. 9 11. -3 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 3 28. 1 Geometry Chapter 8 - Right Triangles
Pythagorean Theorem Name:
Name: 1. A wire reaches from the top of a 13-meter telephone pole to a point on the ground 9 meters from the base of the pole. What is the length of the wire to the nearest tenth of a meter? A. 15.6 C.
5.8 The Pythagorean Theorem
5.8. THE PYTHAGOREAN THEOREM 437 5.8 The Pythagorean Theorem Pythagoras was a Greek mathematician and philosopher, born on the island of Samos (ca. 582 BC). He founded a number of schools, one in particular
7.4 Special Right Triangles
7.4 Special Right Triangles Goal p Use the relationships among the sides in special right triangles. Your Notes The etended ratio of the side lengths of a --908 triangle is 1:1: Ï 2. THEOREM 7.8: --908
Special Right Triangles
GEOMETRY Special Right Triangles OBJECTIVE #: G.SRT.C.8 OBJECTIVE Use trigonometric ratios and the Pythagorean Theorem to solve right triangles in applied problems. *(Modeling Standard) BIG IDEA (Why is
Solving Quadratic Equations (FAL)
Objective: Students will be able to (SWBAT) solve quadratic equations with real coefficient that have complex solutions, in order to (IOT) make sense of a real life situation and interpret the results
Practice 9-1. The Real Numbers. Write all names that apply to each number
Chapter 9 Practice 9-1 The Real Numbers Write all names that apply to each number. 1. 3.2 2. 2 5 3. 12 4. 4 2 5. 20 6. 16 7. 7 8 8. 0.15 9. 18 2 10. 45 11. 25 12. 6.75 State if the number is rational,
Chapter 7. Right Triangles and Trigonometry
Chapter 7 Right Triangles and Trigonometry 4 16 25 100 144 LEAVE IN RADICAL FORM Perfect Square Factor * Other Factor 8 20 32 = = = 4 *2 = = = 75 = = 40 = = 7.1 Apply the Pythagorean Theorem Objective:
CH 21 THE PYTHAGOREAN THEOREM
121 CH 21 THE PYTHAGOREAN THEOREM The Right Triangle A n angle of 90 is called a right angle, and when two things meet at a right angle, we say they are perpendicular. For example, the angle between a
Regional Final. Supervisor s Booklet
Regional Final Supervisor s Booklet Please ensure that students do not have access to this booklet, and take care to hold it so that answers cannot be seen. Mini-Relay Score Sheet School number: School
Math 3 Plane Geometry Review Special Triangles
Name: 1 Date: Math 3 Plane Geometry Review Special Triangles Special right triangles. When using the Pythagorean theorem, we often get answers with square roots or long decimals. There are a few special
Unit 6: Pythagorean Theorem. 1. If two legs of a right triangle are 9 and 11, the hypotenuse is
Name: ate: 1. If two legs of a right triangle are 9 and 11, the hypotenuse is 7. Triangle A is a right triangle with legs that measure 7 and 8. The length of the hypotenuse is 20. 2. 40. 202 15. 113. 9.
Additional Exercises 3.1
Additional Exercises 3.1 Express the statement as an algebraic expression. 1. Fifteen divided by a number x. 1. 2. The difference between a number x and 50 2. 3. The cost C decreased by 14% 3. 4. The profit
Name: Class: Date: Geometry Chapter 4 Test Review
Name: Class: Date: ID: C Geometry Chapter 4 Test Review. 1. Determine the measure of angle UPM in the following figure. Explain your reasoning and show all your work. 3. Determine the side length of each
5-8 Applying Special Right Triangles
5-8 Applying Special Right Triangles Warm Up Lesson Presentation Lesson Quiz Geometry Warm Up For Exercises 1 and 2, find the value of x. Give your answer in simplest radical form. 1. 2. Simplify each
Parallel Lines Cut by a Transversal
Name Date Class 11-1 Parallel Lines Cut by a Transversal Parallel Lines Parallel Lines Cut by a Transversal A line that crosses parallel lines is a transversal. Parallel lines never meet. Eight angles
Parking Lot HW? Joke of the Day: What do you call a leg that is perpendicular to a foot? Goals:
Parking Lot Joke of the Day: HW? What do you call a leg that is perpendicular to a foot? a right ankle Goals: Agenda 1 19 hw? Course Recommendations Simplify Radicals skill practice L8 2 Special Right
Chapter 10. Right Triangles
Chapter 10 Right Triangles If we looked at enough right triangles and experimented a little, we might eventually begin to notice some relationships developing. For instance, if I were to construct squares
Perimeter. Name. 22 Topic 17. Reteaching Find the perimeter of the figure below.
Perimeter Reteaching 1-1 Find the perimeter of the figure below. 15 m x 4 ft 4 ft 2 ft y 2 ft 5 ft 6 m 20 ft Reteaching 1-1 By using a formula: There are two equal lengths and equal widths, so you can
Similar Right Triangles
MATH 1204 UNIT 5: GEOMETRY AND TRIGONOMETRY Assumed Prior Knowledge Similar Right Triangles Recall that a Right Triangle is a triangle containing one 90 and two acute angles. Right triangles will be similar
Student Resource / Program Workbook INTEGERS
INTEGERS Integers are whole numbers. They can be positive, negative or zero. They cannot be decimals or most fractions. Let us look at some examples: Examples of integers: +4 0 9-302 Careful! This is a
Student Outcomes. Lesson Notes. Classwork. Discussion (20 minutes)
Student Outcomes Students explain a proof of the converse of the Pythagorean Theorem. Students apply the theorem and its converse to solve problems. Lesson Notes Students had their first experience with
Warm Up Find what numbers the following values are in between.
Warm Up Find what numbers the following values are in between. 1. 30 2. 14 3. 55 4. 48 Color squares on each side of the triangles with map pencils. Remember A square has 4 equal sides! Looking back at
1. If x represents a number, six ubtracted from four times the number can be represented by
Math 60, HW 13 Section 2.5 Name: Concept and Vocabulary: 1. If x represents a number, six ubtracted from four times the number can be represented by 2. According to F orbes magazine, the top-earning dead
CK-12 Geometry: Special Right Triangles
CK-12 Geometry: Special Right Triangles Learning Objectives Identify and use the ratios involved with isosceles right triangles. Identify and use the ratios involved with 30-60-90 triangles. Review Queue
Related Rates - Classwork
Related Rates - Classwork Earlier in the year, we used the basic definition of calculus as the mathematics of change. We defined words that meant change: increasing, decreasing, growing, shrinking, etc.
Student Instruction Sheet: Unit 4, Lesson 4. Solving Problems Using Trigonometric Ratios and the Pythagorean Theorem
Student Instruction Sheet: Unit 4, Lesson 4 Suggested Time: 75 minutes Solving Problems Using Trigonometric Ratios and the Pythagorean Theorem What s important in this lesson: In this lesson, you will
Section 8: Right Triangles
The following Mathematics Florida Standards will be covered in this section: MAFS.912.G-CO.2.8 Explain how the criteria for triangle congruence (ASA, SAS, SSS, and Hypotenuse-Leg) follow from the definition
GCSE 9-1 Higher Edexcel Set C Paper 1 - Non Calculator
Name: GCSE 9-1 Higher Edexcel Set C Paper 1 - Non Calculator Equipment 1. A black ink ball-point pen. 2. A pencil. 3. An eraser. 4. A ruler. 5. A pair of compasses. 6. A protractor. Guidance 1. Read each
Areas of Parallelograms and Triangles 7-1
Areas of Parallelograms and Triangles 7-1 Parallelogram A parallelogram is a quadrilateral where the opposite sides are congruent and parallel. A rectangle is a type of parallelogram, but we often see
5. Find two numbers whose sum is 48 and whose product is to be a maximum.
1 Optimization Practice (4.4) 1. If 40 passengers hire a special car on a train, they will be charged $8 each. This fare will be reduced by $.10 each passenger, for each person in addition to these 40.
Lesson 21: Special Relationships within Right Triangles Dividing into Two Similar Sub-Triangles
: Special Relationships within Right Triangles Dividing into Two Similar Sub-Triangles Learning Targets I can state that the altitude of a right triangle from the vertex of the right angle to the hypotenuse
Sum Fun Tournament Meeting (Multiple Topics)
Sum Fun Sum Fun Tournament Meeting (Multiple Topics) Sum Fun Topic There are a wide range of topics and difficulty levels covered during this meeting. Materials Needed The first four items listed below
8-1. The Pythagorean Theorem and Its Converse. Vocabulary. Review. Vocabulary Builder. Use Your Vocabulary
8-1 The Pythagorean Theorem and Its Converse Vocabulary Review 1. Write the square and the positive square root of each number. Number 9 Square Positive Square Root 1 4 1 16 Vocabulary Builder leg (noun)
word problems.notebook May 27, 2016
Word Problems: When solving word problems you can use vertex form, factored form or standard form to create an algebraic model of the situation. Use the form that is most helpful for the context of the
MORE TRIGONOMETRY
MORE TRIGONOMETRY 5.1.1 5.1.3 We net introduce two more trigonometric ratios: sine and cosine. Both of them are used with acute angles of right triangles, just as the tangent ratio is. Using the diagram
Free Response Review
Name Free Response Review 1. A rescue team 1000 ft. away from the base of a vertical cliff measures the angle of elevation to the top of the cliff to be 70. A climber is stranded on a ledge. The angle
Unit 2: Right Triangle Trigonometry RIGHT TRIANGLE RELATIONSHIPS
Unit 2: Right Triangle Trigonometry This unit investigates the properties of right triangles. The trigonometric ratios sine, cosine, and tangent along with the Pythagorean Theorem are used to solve right
21st AMC (A) 1 (B) 2 (C) 3 (D) 4 (E) 5
21st AMC 8 2005 2 1. Connie multiplies a number by 2 and gets 60 as her answer. However, she should have divided the number by 2 to get the correct answer. What is the correct answer? (A) 7.5 (B) 15 (C)
What s the distance that a person would have to walk to get from Holy Cross to where Robbins was arrested?
Page 1 of 6 Try Now: In 2005, the Pythagorean Theorem was a deciding factor in a case before the New York State Court of Appeals. A man named Robbins was convicted of selling drugs within 1000 of a school.
ROUND TOSSUP: What is twenty-five percent of sixty? (15) (10 pts)
ROUND 1 1. TOSSUP: Giving your answer in the correct unit, what is the area of a rectangle whose length is 7 inches and whose width is 4 inches? (28 square inches) (10 pts) FOLLOWUP: Abe walked halfway
(a) (First lets try to design the set of toy s the easy way.) The easiest thing to do would be to pick integer lengths for the lengths of the sticks.
Name: Elementary Functions K nex AAP (Pythagorean theorem, function composition) My son has a set of construction toys called K nex. In this problem you will think like the designers of these toys. The
12-2 Area of Circles. Find the area of each circle. Round to the nearest tenth. 1. ANSWER: m 2. ANSWER: 12.6 yd 2 ANSWER: 132.
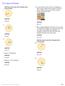Find the area of each circle. Round to the nearest tenth. 1. 6. A motion detector at the corner of a building can detect motion outside within a radius of 20 feet as shown. Within what area can it detect
Geometry: Pythagoras theorem
Geometry: Pythagoras theorem. Pythagoras theorem HOMWORK In each of the following triangles, find the hypotenuse, rounding off to a suitable degree of accuracy. a b c 5. cm cm. cm cm 3 cm 3.7 cm d e f.
1. Five more than three times a number x. 3. Seventeen percent of a number x.
Pre-Calculus: 1.7.1 Mastery Practice Name: Date Period Write a mathematical expression for the quantity described verbally: 1. Five more than three times a number x. 3. Seventeen percent of a number x.
Geometry Chapter 7 Review Right Triangles Use this review to help prepare for the Chapter 7 Test. The answers are attached at the end of the document.
Use this review to help prepare for the hapter 7 Test. The answers are attached at the end of the document. 1. Solve for a and b. 2. Find a, b, and h. 26 24 a h b 10 b a 4 12. The tangent of is. 4. A is
ROUND TOSS-UP: What is the square root of one million? (1000) (10 points) BONUS: How many zeros are at the end of ?
ROUND 1 1. TOSS-UP: What is 24% of 50? (12) (10 points) BONUS: A clothing store is having a 60% off sale on its dresses. Brandi has a coupon that lets her take 20% off of the sale price. If she pays $24
2011 Canadian Intermediate Mathematics Contest
The CENTRE for EDUCATION in MATHEMATICS and COMPUTING www.cemc.uwaterloo.ca 011 Canadian Intermediate Mathematics Contest Tuesday, November, 011 (in North America and South America) Wednesday, November
TEST NAME: G.7 TEST ID: GRADE:08 Eighth Grade SUBJECT: Mathematics TEST CATEGORY:School Assessment
TEST NAME: G.7 TEST ID:877132 GRADE:08 Eighth Grade SUBJECT: Mathematics TEST CATEGORY:School Assessment G.7 Page 1 of 89 Student: Class: Date: 1. Mr. Lopez has a rectangular classroom that measures 36
7 The Pythagorean Theorem
HPTER 7 The Pythagorean Theorem Lesson 7.1 Understanding the Pythagorean Theorem and Plane Figures For each figure, shade two right triangles and label the hypotenuse of each triangle with an arrow. 1.
Pythagorean Theorem Review Missing Hypotenuse. Name: Mr. Fourmy.
Name: Mr. Fourmy Date: Period: -------------------------- ---------------- Pythagorean Theorem Review Missing Hypotenuse --------- Directions: Using the Pythagorean Theorem.jind the missing side length/or
Chapter 7: Quadratics
Chapter 7: Quadratics Notes 7.8 Quadratic Modeling Name: Set up a quadratic equation to model the scenario and use ANY method to solve: Vertex Form to find max/min or symmetry Factoring to find zeros/solutions
A life not lived for others is not a life worth living. Albert Einstein
life not lived for others is not a life worth living. lbert Einstein Sides adjacent to the right angle are legs Side opposite (across) from the right angle is the hypotenuse. Hypotenuse Leg cute ngles
Downloaded From GovernmentAdda.com India s #1 Study Hub Lakshmi Vilas Bank Limited (LVB) Quantitative aptitude questions
Lakshmi Vilas Bank Limited (LVB) Quantitative aptitude questions 1 (95.6x 910.3) 92.56256 = 9? (A) 13.14 (B) 12.96 (C) 12.43 (D) 13.34-Answer 2. (4 86%of 6500) 36 =? (A) 867.8 (B) 792.31 (C) 877.5-Answer
Experiences with Area Assessment Materials
Experiences with Area Assessment Materials 1. Jenny bought a rectangular rug that had an area of 24 square feet and a perimeter of 20 feet. Which model shows the correct dimensions of the rug? A. 8 feet
COMPACTED MATHEMATICS CHAPTER 10 AREA AND PERIMETER TOPICS COVERED:
COMPACTED MATHEMATICS CHAPTER 10 AREA AND PERIMETER TOPICS COVERED: Perimeter of polygons Area of rectangles and squares Area of parallelograms Area of triangles Area of trapezoids Activity 10-1 Perimeter
Math 15 Test 3 Review Section Change 4.5 yards to inches. Round your answer to the nearest inch. (1 yd = 3 ft, 1 ft = 12 in)
Page 1 Math 15 Section 6.3 18. Change 4.5 yards to inches. Round your answer to the nearest inch. (1 yd = 3 ft, 1 ft = 12 in) 30. Change 528 inches to feet. (1 ft = 12 in) 42. Change 3 1/16 pounds to ounces.
The Pythagorean Theorem Diamond in the Rough
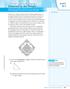The Pythagorean Theorem SUGGESTED LEARNING STRATEGIES: Shared Reading, Activating Prior Knowledge, Visualization, Interactive Word Wall Cameron is a catcher trying out for the school baseball team. He
9.3 Altitude-on-Hypotenuse Theorems
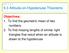9.3 Altitude-on-Hypotenuse Theorems Objectives: 1. To find the geometric mean of two numbers. 2. To find missing lengths of similar right triangles that result when an altitude is drawn to the hypotenuse
8-1. The Pythagorean Theorem and Its Converse. Vocabulary. Review. Vocabulary Builder. Use Your Vocabulary
8-1 he Pythagorean heorem and Its Converse Vocabulary Review 1. Write the square and the positive square root of each number. Number Square Positive Square Root 9 81 3 1 4 1 16 1 2 Vocabulary Builder leg
Bishop Kelley High School Summer Math Program Course: Trigonometry and Trigonometry with Pre-Calculus
015 01 Summer Math Program Course: Trigonometr and Trigonometr with Pre-Calculus NAME: DIRECTIONS: Show all work on loose-leaf paper, which ou will turn in with the packet. (NO WORK IN PACKET!) Put final
1. I: 3. M: 5. C: about m 6. T: m. 7. O: about. 9. O: about m 10. COMPOSITE cm cm
8.4 Warm Up For use before Activity 8.4. 100 ft. 150 m 56 in. 0 cm 5. about 14 ft 6. about 7850 yd 8.4 Start Thinking! For use before Lesson 8.4 Check students drawings and calculations. 8.4 Warm Up For
March 01, Applications of Rt triangle trig ink.notebook. 8.4 Applications of Rt Triangle Trig. Standards
Lesson Objectives Standards Lesson Notes Lesson Objectives Standards Lesson Notes 8.4 Applications of Rt Triangle Trig After this lesson, you should be able to successfully find and use trigonometric ratios
Week 11, Lesson 1 1. Warm Up 2. Notes Sine, Cosine, Tangent 3. ICA Triangles
Week 11, Lesson 1 1. Warm Up 2. Notes Sine, Cosine, Tangent 3. ICA Triangles HOW CAN WE FIND THE SIDE LENGTHS OF RIGHT TRIANGLES? Essential Question Essential Question Essential Question Essential Question
June x. 2. x. 3. x. Sunday Monday Tuesday Wednesday Thursday Friday Saturday 8.NS.1 8.NS.1 8.NS.1 8.NS.1 8.NS /3 + 1/9 2.
June 2018 Sunday Monday Tuesday Wednesday Thursday Friday Saturday 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 Father s Day 24 25 26 27 28 29 30 1. 1/3 + 1/9 2. 1 8/9 + 3 2/3 3. 9 6/7 +
Word Problems: Number Theory and past/future Alg. 1H
PS-A1 Word Problems: Number Theory and past/future Alg. 1H DO ON BINDER PAPER Define variables ("Let Statements"). Write a verbal model. Write an equation. Then solve your equation. Finally answer the
Algebra A/B MAT 035. Review for Final Exam
Computation: Evaluate the following expressions: 1. 5-7 + (-8) - (-3) 2 2. -5 (-3) (2) (-5) 3. 4. 5. 11 2 23 + 24 6. 7. (14-3) (3-7) +2 (3-9) 8. 7-2[ ] 9. 20-12 2 3-10. -8[ -4 6 (4-7)] 11. 12 4[7 3(6 2)]
Perimeter. Perimeter is the distance around a shape. You can use grid. Step 1 On grid paper, draw a rectangle that has a length
Lesson 13.1 Perimeter Perimeter is the distance around a shape. You can use grid paper to count the number of units around the outside of a rectangle to find its perimeter. How many feet of ribbon are
2011 Excellence in Mathematics Contest Team Project Level I (Precalculus and above) School Name: Group Members:
011 Excellence in Mathematics Contest Team Project Level I (Precalculus and above) School Name: Group Members: Reference Sheet Formulas and Facts You may need to use some of the following formulas and
Simplifying Radical Expressions and the Distance Formula
1 RD. Simplifying Radical Expressions and the Distance Formula In the previous section, we simplified some radical expressions by replacing radical signs with rational exponents, applying the rules of
Jefferson Township Public Schools Mathematics Department
Jefferson Township Public Schools Mathematics Department Dear Student of Math Investigations, Your first assignment as a Math Investigations student will be the summer assignment. This packet is a review
2017 AMC 12B. 2. Real numbers,, and satisfy the inequalities,, and. Which of the following numbers is necessarily positive?
2017 AMC 12B 1. Kymbrea's comic book collection currently has 30 comic books in it, and she is adding to her collection at the rate of 2 comic books per month. LaShawn's comic book collection currently
EQ: GPE.7 How do I find the perimeter and area of polygons?
EQ: GPE.7 How do I find the perimeter and area of polygons? Essential Question Essential Question Essential Question Essential Question Essential Question Essential Question Essential Question Week 14,
1ACE Exercise 4. Name Date Class
1ACE Exercise 4 Investigation 1 4. A farm wants to add a small rectangular petting zoo for the public. They have a fixed amount of fencing to use for the zoo. This graph shows the lengths and areas of
Parking Lot HW? Joke of the Day: What do you get when you combine a flat, infinite geometric figure with a beef patty?
Parking Lot HW? Joke of the Day: What do you get when you combine a flat, infinite geometric figure with a beef patty? a plane burger Agenda 1 23 hw? Finish Special Right Triangles L8 3 Trig Ratios HW:
Practice Test. 2 What is the area of this figure?
Practice Test 1 Which letter has a line of symmetry? S J R W L 3 Jane's house has a garden which is in the shape of a square. If each side of the garden is 18 feet then what is the perimeter of the garden?
Tilden Middle School Summer Math Packet Incoming Grade 6
Tilden Middle School Summer Math Packet Incoming Grade 6 . Several expressions are shown. Decide if the value of the expression is less than, equal to, or greater than 5. Write the expressions in the corresponding
More Word Problems. Front 19 x 19x. Rear 14 x (x + 525) Solve: 19x + 14(x + 525) = 31, front and 1265 rear
Name: Date: More Word Problems 1) Tickets to a concert were $19 for the seats near the front and $14 for the rear seats. There were 525 more rear seats sold than front seats, and sales for all tickets
Mathacle PSet Algebra Word Problems ( ) Level Number Name: Date:
Translate each problem into an equation. Then solve the equation. 1.) Howard works an 8-hour day at his gas station. He spends twice as much time working on cars as he does waiting on customers. He takes
Name. STAR CITY Math / Geometry / Special Right Triangles. Teacher Period. Use the diagram below to answer question 1.
STAR CITY Math / Geometry / Special Right Triangles Use the diagram below to answer question 1. Name Teacher Period 2. The drawing shows the measurements in a section of a circular design. How long is
2011 Excellence in Mathematics Contest Team Project Level I (Precalculus and above)
011 Excellence in Mathematics Contest Team Project Level I (Precalculus and above) School Name: Solutions Group Members: Reference Sheet Formulas and Facts You may need to use some of the following formulas
1. A right triangle has legs of 8 centimeters and 13 centimeters. Solve the triangle completely.
9.7 Warmup 1. A right triangle has legs of 8 centimeters and 13 centimeters. Solve the triangle completely. 2. A right triangle has a leg length of 7 in. and a hypotenuse length of 14 in. Solve the triangle
Lesson 6.1 Assignment
Lesson 6.1 Assignment Name Date Soon You Will Determine the Right Triangle Connection The Pythagorean Theorem 1. Lamar goes shopping for a new flat-panel television. A television is usually described by
Right is Special 1: Triangles on a Grid
Each student in your group should have a different equilateral triangle. Complete the following steps: Using the centimeter grid paper, determine the length of the side of the triangle. Write the measure
Grade 7 & 8 Math Circles Pair-O -Dice: The Game April 2/3, 2013
Faculty of Mathematics Waterloo, Ontario N2L 3G1 Instructions Set Up Grade 7 & 8 Math Circles Pair-O -Dice: The Game April 2/3, 2013 Get into a group of 3 to 5 players. Each group needs 2 different dice
Arithmetic with Units of Measure
Arithmetic with Units of Measure Reteaching 81 Math Course 1, Lesson 81 If units are not the same, convert first. Example: 2 ft + 12 in. 24 in. + 12 in. or 2 ft + 1 ft To add or subtract measures, keep
2018 Chapter Competition Countdown Round Problems 1 80
2018 Chapter Competition Countdown Round Problems 1 80 This booklet contains problems to be used in the Countdown Round. 2018 MATHCOUNTS National Competition Sponsor National Sponsors Raytheon Company