The Pythagorean Theorem and Its Converse Is That Right?

Transcription

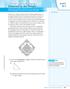
1 The Pythgoren Theorem nd Its Converse Is Tht Right? SUGGESTED LEARNING STRATEGIES: Activting Prior Knowledge, Mrking the Text, Shred Reding, Summrize/Prphrse/Retell ACTIVITY 3.6 How did Pythgors get theorem nmed fter him? Although mny exmples of the Pythgoren Theorem were known nd used y the Bylonins, Chinese, Hindu nd Egyptins well efore Pythgors ws orn (out 570 BCE), he is given credit for eing the first to formlly prove the theorem. Mny others since Pythgors time, including young mn nmed Jmes Grfield who would go on to e President of the United Sttes, hve lso offered forml proofs of the well known theorem. Exmine one proof of the Pythgoren Theorem tht is credited to Pythgors himself. Begin with squre hving edges of length +. In the squre, four right tringles with legs nd hve een drwn. M R N O P ACADEMIC VOCABULARY THE PYTHAGOREAN THEOREM In ny right tringle, the squre of the length of the hypotenuse is equl to the sum of the squres of the lengths of the legs. If nd re the lengths of the legs nd c is the length of the hypotenuse then, c 2 = S T Q 2010 College Bord. All rights reserved. 1. Ech of the four right tringles in the digrm ove re congruent. Wht tringle congruence method justifies this sttement? Explin your nswer. 2. Since the four right tringles re congruent, we know their hypotenuses, RN, TR, PT nd NP, re congruent.. Wht reson cn e used to justify this?. Lel ech hypotenuse in the digrm, c. Unit 3 Similrity, Right Tringles, nd Trigonometry 235

2 ACTIVITY 3.6 The Pythgoren Theorem nd Its Converse Is Tht Right? SUGGESTED LEARNING STRATEGIES: Activting Prior Knowledge, Look for Pttern, Quickwrite 3. MNR is right tringle nd MNR SRT.. Wht is the reltionship etween MRN nd MNR? How do you know?. Use the congruence sttement, MNR SRT. Wht does this indicte out the reltionship etween MRN nd SRT? Explin your resoning. c. Wht kind of ngle is NRT? How do you know? d. Wht re the mesures of RTP, TPN nd PNR? Justify your nswer. 4. Wht specil qudrilterl is formed y the four hypotenuses? Justify your nswer College Bord. All rights reserved. 236 SpringBord Mthemtics with Mening Geometry

3 The Pythgoren Theorem nd Its Converse Is Tht Right? ACTIVITY 3.6 SUGGESTED LEARNING STRATEGIES: Think/Pir/Shre, Crete Representtions 5. It cn e ssumed from the digrm tht the re of the lrge outside squre is equl to the sum of the res of the four tringles nd qudrilterl PNRT. Write n eqution, in terms of,, nd c tht represents this sttement. 6. Use lgeric properties to simplify oth sides of the eqution. 7. Solve the simplified eqution for c 2. You hve now verified lgericlly, much s Pythgors is thought to hve done, The Pythgoren Theorem nd cn use it to solve prolems College Bord. All rights reserved. 8. How high up verticl wll will 24 foot ldder rech if the foot of the ldder is plced 10 feet from the wll? Drw sketch nd show the clcultions tht support your nswer. Unit 3 Similrity, Right Tringles, nd Trigonometry 237

4 ACTIVITY 3.6 The Pythgoren Theorem nd Its Converse Is Tht Right? SUGGESTED LEARNING STRATEGIES: Activting Prior Knowledge, Close Reding, Mrking the Text, Think/Pir/ Shre, Self/Peer Revision 9. Find the re of rectngulr rug if the width of the rug is 13 feet nd the digonl mesures 20 feet. Drw sketch nd show the clcultions tht support your nswer. The Pythgoren Theorem sttes tht, in right tringle, the squre of the length of the hypotenuse is equl to the sum of the squres of the lengths of the legs. Is the converse of this sttement true? 10. Write the Pythgoren Theorem in if-then form. 11. Write the converse of the Pythgoren Theorem in if-then form. 12. Cn the converse of the Pythgoren Theorem e proven? Assume you hve ABC where c 2 = 2 + 2, s shown elow. Complete the following to try to prove ABC is right tringle. Use right DEF, with legs nd nd hypotenuse f. B C c A E F f D 2010 College Bord. All rights reserved. 238 SpringBord Mthemtics with Mening Geometry

5 The Pythgoren Theorem nd Its Converse Is Tht Right? ACTIVITY 3.6 SUGGESTED LEARNING STRATEGIES: Activting Prior Knowledge, Close Reding, Group Presenttion, Quickwrite. It is known tht f 2 = Give reson for this sttement.. It ws ssumed tht in ABC, c 2 = So, the sttement c = f cn e mde. Why is this true? c. ABC DEF y wht reson? d. C is right ngle. Give reson for this sttement. e. ABC is right tringle. Wht reson justifies this sttement? 2010 College Bord. All rights reserved. 13. You exmined the converse of the Pythgoren Theorem. Now, tke look t the inverse.. Write the inverse of the Pythgoren Theorem in if-then form.. Is the inverse true sttement? Why or why not? Unit 3 Similrity, Right Tringles, nd Trigonometry 239

6 ACTIVITY 3.6 The Pythgoren Theorem nd Its Converse Is Tht Right? SUGGESTED LEARNING STRATEGIES: Use Mnipultives Since you hve shown the Converse of the Pythgoren Theorem is true, little more explortion follows. 14. Use ech of the following sets of tringle side lengths to uild tringles using the mnipultives (strws) provided y your techer. Step 1: Step 2: Step 3: Step 4: Cut mnipultives into 5 cm, 6 cm, 12 cm, 13 cm, nd 15 cm lengths. Build ech tringle on centimeter grid pper. Identify ech tringle s right, cute or otuse. Complete the tle. Tringle side lengths Type of tringle c , 12, 13 6, 6, 12 5, 6, 12 5, 12, 15 5, 12, 12 6, 12, 13 6, 12, College Bord. All rights reserved. 240 SpringBord Mthemtics with Mening Geometry

7 The Pythgoren Theorem nd Its Converse Is Tht Right? ACTIVITY 3.6 SUGGESTED LEARNING STRATEGIES: Think/Pir/Shre, Look for Pttern 15. Wht does your work in Item 14 suggest out the reltionship etween 2, 2, c 2 nd the type of tringle? 16. Use the Converse of the Pythgoren Theorem to determine whether ech of the following sets of side lengths forms right tringle. If right tringle is not possile, tell whether n cute or otuse tringle cn e formed. Show the method you use to determine your nswers.. 12, 34, , 7 8, 10 7 c. 20, 42, College Bord. All rights reserved. Unit 3 Similrity, Right Tringles, nd Trigonometry 241

8 ACTIVITY 3.6 The Pythgoren Theorem nd Its Converse Is Tht Right? SUGGESTED LEARNING STRATEGIES: Activting Prior Knowledge Another wy to prove the Pythgoren theorem is y using tringle similrity. In right tringle ABC elow, n ltitude is drwn to hypotenuse AB, forming two right tringles tht re similr to tringle ABC. C h A x c x B Corresponding sides of similr tringles re in proportion, so you cn write these proportions involving sides of the tringles. x = c c x = c 17. Use the proportions ove nd lger to prove = c 2. c CHECK YOUR UNDERSTANDING Write your nswers on on noteook pper pper. or on Show grid your work. 3. Tell whether tringle cn e formed hving pper. Show your work. the following side lengths. If tringle cn e formed tell whether it is right, cute or otuse. 1. If television screen is rectngle with 53 inch digonl nd width of 45 inches, wht is the height of the screen? 2. A stndrd sell dimond is squre 90 feet on ech side. Find the distnce of throw mde from the ctcher 3 feet ehind home plte in n ttempt to throw out runner trying to stel second se. Round to the nerest whole numer.. 93 feet. 124 feet c. 130 feet d. 183 feet. 4, 6, 8. 8, 8, MATHEMATICAL REFLECTION The Pythgoren Theorem ws thought of y the erly Greeks s the following: The re of the squre on the hypotenuse of right tringle is equl to the sum of the res of the squres on the legs. Drw digrm to illustrte this sttement. Explin how your digrm illustrtes the Pythgoren Theorem College Bord. All rights reserved. 242 SpringBord Mthemtics with Mening Geometry