This article appeared in a journal published by Elsevier. The attached copy is furnished to the author for internal non-commercial research and
|
|
|
- Lynne Burke
- 5 years ago
- Views:
Transcription
1 This article appeared in a journal published by Elsevier. The attached copy is furnished to the author for internal non-commercial research and education use, including for instruction at the authors institution and sharing with colleagues. Other uses, including reproduction and distribution, or selling or licensing copies, or posting to personal, institutional or third party websites are prohibited. In most cases authors are permitted to post their version of the article (e.g. in Word or Tex form) to their personal website or institutional repository. Authors requiring further information regarding Elsevier s archiving and manuscript policies are encouraged to visit:
2 Measurement 42 (2009) Contents lists available at ScienceDirect Measurement journal homepage: Development of a wearable sensor system for quantitative gait analysis Tao Liu *, Yoshio Inoue, Kyoko Shibata Department of Intelligent Mechanical Systems Engineering, Kochi University of Technology, 185 Miyanokuchi, Tosayamada-cho, Kami-city, Kochi , Japan article info abstract Article history: Received 10 July 2007 Received in revised form 17 July 2008 Accepted 16 February 2009 Available online 23 February 2009 Keywords: Quantitative gait analysis Wearable sensor system Gait phases This paper presents a study on development of a wearable sensor system for quantitative gait analysis using inertial sensors of gyroscopes and accelerometers. This system was designed to detect gait phases including initial contact, loading response, mid stance, terminal stance, pre swing, initial swing, mid swing and terminal swing, which is quite inexpensive compared with conventional 3D motion analysis systems based on high-speed cameras. Since conventional camera-based systems require costly devices, vast space as well as time-consuming calibration experiments, the wearable sensor-based system is much cheaper. Gyroscopes (ENC-05EB) and two-axis ADXL202 accelerometers are incorporated in this wearable sensor system. The former are attached on the surface of the foot, shank and thigh to measure the angular velocity of each segment, and the latter are used to measure inclination of the attached leg segment (shank) in every single human motion cycle for recalibration. The gyroscope is sensitive to a temperature change or small changes in the structure (mechanical wear), which leads to fluctuating offsets from sensor output in applications of human motion measurements. The orientation estimation algorithm here continuously corrects orientation estimates obtained by mathematical integration of the angular velocity measured using the gyroscopes. Correction is performed using an inclination estimation obtained using the signal of the two-axis accelerometer during the interval of mid stance in each stride. The average of root mean squared error (RMSE) was not over 5.0 (the thigh angle orientation) when the calibration was implemented. Correlation coefficient (R) approached 0.9 when the segment angles obtained from the wearable sensor system were compared with the results from a conventional optical motion analysis system. Ó 2009 Elsevier Ltd. All rights reserved. 1. Introduction 1.1. Research background The standard method for human motion analysis is optical motion analysis using high-speed cameras to capture human motion. The integration of three-dimensional motion measurement using multi-camera systems and reaction force measurement using force plates has been successfully developed to tracking human body parts and performing dynamics analysis of their physical behaviors in a complex environment [1,2]. However, the optical * Corresponding author. Tel./fax: address: liu.tao@kochi-tech.ac.jp (T. Liu). motion analysis method needs considerable work space and high-speed graphic signal processing devices, and using this analysis method, the devices are expensive, and pre-calibration experiments and off-line analysis of recorded pictures are especially complex and time consuming. Therefore, this method and the other standard systems using magnetic or sonic technologies are limited to laboratory research, and are difficult to be applied in daily life applications or complex environments. Moreover, the human body is composed of many highly flexible segments, and the upper-body motion of human is especially complicated in terms of accuracy calculations. Thus, wearable sensor system with properties of lower cost, friendly operation and less effect to human is becoming an important topic in biomechanics and clinical applications /$ - see front matter Ó 2009 Elsevier Ltd. All rights reserved. doi: /j.measurement
3 T. Liu et al. / Measurement 42 (2009) To implement home-based rehabilitation and tele-rehabilitation, some researchers have developed many kinds of wearable (body-fixed) sensor system based to single accelerometers or multi-accelerometer and gyroscope combinations [3 6]. Moreover, for monitoring activities of daily living of disabled person and providing life support, new techniques using different types of ambulatory sensor systems can be helpful outside of a laboratory [7 10]. Recent research on wearable sensor systems for biomedical applications can be divided into two major directions: one is about state recognition on daily physical activities including walking feature assessment [11,12], walking condition classification [13 16] and gait phase detection [17 20], in which the kinematic data obtained from inertial sensors (accelerometer or gyroscope) are directly used as inputs of some inference techniques; and another direction is for accurate measurement of human motion such as joint angle, body segment 3D position and orientation, in which measurement calibration and data fusing of different inertial sensors are important to decrease errors of the quantitative human motion analysis. In our research, a wearable sensor system for human motion and ground reaction force measurement will be developed to estimate joint moment and muscle tension force, so we are focusing on the second direction for quantitative human motion analysis. There are growing interests in adopting commercial products of 3D motion sensor system, for example, smart sensor module MTx (Xsens, The Netherlands) [21] that realized a motion sensor by three angular rate sensors three accelerometers and three magnetic sensors, can reconstruct tri-axial angular displacements by means of a dedicated algorithm. However, it is sensitive to effect of magnetic filed environment, and the dynamic accuracy of this sensor is two degree RMS which depends on type of motion conditions. Using accelerometer and gyroscope combination without magnetic sensors, Dejnabadi et al., Williamson et al. and Favre et al. introduced some methods to estimate absolute joint angles without hindrance to natural activities [22 24]; however, segment orientation or joint position is very important information for some human dynamics analysis applications like joint moment estimation [25]. Sabatini et al. as well other authors (Luinge et al.) have proposed algorithms based to strap-down integration for foot orientation estimation by considering inclination during stance phase as initial condition for the integration of angular velocity [26 29]. Dejnabadi et al. also presented a method in [30] to estimate lower limbs orientations using a combination of accelerometers and gyroscopes, in which virtual sensors [22] were used to estimate joint angles, then by fusing the data of accelerometers regarded as goniometers during lower body motion acceleration, stable and drift-free estimation of segment orientation was implemented. As all the authors stated, there is a need of cycle rectification from data of accelerometer for strap-down integration method based to gyroscope measurement, but because of lower precision of accelerometer in dynamic condition and some special application like measurement for paralytic patient where the heel may never contact the ground, cyclically using of data of accelerometer in dynamic condition may be difficult to decrease error during orientation estimation. Some regression networks algorithms were introduced in [31,32] as another resolution for predicting the segmental orientations using wearable measurement devices such as gyroscopes and accelerometers, and the effect of loss of sensor data on lower limbs kinematics prediction was addressed. In this paper, based on the precision measurement of accelerometer during static situation and a linear regression method for simplified assessment of drift error, we proposed a motion analysis system with intelligent calibration for quantitative gait analysis including gait phase detection and leg segment orientation estimation. This motion analysis system is the combination of three gyroscopes that measure the rotational velocity of the foot, shank and thigh, and a two-axis accelerometer that can detect angle of inclination from measurements of twodirectional accelerations projected by gravity acceleration. An error estimation algorithm based on results of direct digital integration of gyroscope signals and segment angles of inclination measured by accelerometer in the static states of human walking, was developed to continuously correct orientation estimates obtained by mathematical integration of the angular velocity measured using gyroscopes. Gait analysis results including leg segment orientation obtained with this motion analysis system were compared with the motion analysis results obtained using a commercial optical motion analysis system Introduction of gait phase In the past it has been the custom to use normal events as the critical actions separating gait phases. While this practice proved appropriate for the amputee, it often failed to accommodate the gait deviations of patients impaired by paralysis or arthritis. For example, the onset of stance customarily has been called heel strike [18,19]; yet the heel of a paralytic patient may never contact the ground or do so much later in the gait cycle. Similarly initial floor contact may be by the whole foot (foot flat), rather than having forefoot contact occur later, after a period of heel-only support. To avoid these difficulties and other areas of confusion, the Rancho Los Amigos gait analysis committee developed a generic terminology for the functional phases of gait [33]. Analysis of human walking pattern by phases more directly identifies the functional significance of the different motions accruing at the individual joints and segments. In this paper, a normal walking gait cycle is divided into eight different gait phases including initial contact, loading response, mid stance, terminal stance, pre-swing, initial swing, mid swing and terminal swing (as shown in Fig. 1) [34]. In the following discussion, we assume that the subjects are viewed from the right lateral side and anticlockwise rotations are considered positive. h f ; h s and h t represent the inclination angles of the foot, shank and thigh with respect to gravity direction, respectively. x f ; x s and x t represent the angular velocities of the foot, shank and thigh in the lateral plane, respectively. Finally, e h ; e x and e a represent small threshold values for the detection of close to zero angle displacements, angular velocities and accelerations, respectively.
4 980 T. Liu et al. / Measurement 42 (2009) a Initial contact Loading response Mid stance Terminal stance z y x Sensor unit III: Single-axis gyroscope sensitive to y- pitch velocity Knee joint b Preswing Initial swing Mid swing Terminal swing z y x z y x Ankle joint Toe joint Sensor unit II: Single-axis gyroscope and two-axis Accelerometer for shank motion Sensor unit I: Single-axis gyroscope sensitive to y- pitch velocity Fig. 1. (a) Gait phases of stance period. (b) Gait phases of swing period. Each of the eight gait phase has a functional objective and a critical pattern of selective synergistic motion to accomplish this goal. The sequential combination of the phases also enables the lime to accomplish three basic tasks, which include weight acceptance, single limb support and limb advancement. Weight acceptance begins the stance period and uses phases of initial contact and loading response. Single limb support continues stance with phases of mid stance and terminal stance. Limb advancement begins in phase of pre-swing and then continues through the three phases of initial swing, mid swing and terminal swing. Fig. 2. Position and coordinates of the sensor units. In the local orientation coordinate of the sensor unit (X-, Y- and Z-axis), Y-axis denotes each joint s rocker axis, which is parallel to the sensitive axis of the gyroscope, while X-axis and Z-axis denote the unity vectors in the radial and tangential direction, respectively. Multi-channel Data- recorder 2. Methods and materials 2.1. Sensor system As shown in Fig. 2, three gyroscopes are used to measure angular velocities of leg segments of foot, shank and thigh (x 1, x 2 and x 3 Þ. The sensing axis is vertical to the medial lateral plane so that the angular velocity in the sagittal plane can be detected. In local coordinates of three segments, sensing axis of the gyroscopes is along y-axis, and the z-axis is along leg-bone. A two-axis accelerometer is attached on the side of shank to measure two-directional accelerations along tangent direction of x-axis ða t Þ and sagittal direction of z-axis ða r Þ. In this system, the data from accelerometer are fused with data collected from gyroscopes for cycle system calibration, through supplying initial angular displacement of the attached leg segment Hardware system design As shown in Fig. 3, the wearable sensor system includes an eight-channel data recorder (size, 110 mm 60 mm 20 mm; weight including cables, 200 g), a gyroscope and accelerometer combination unit and two gyroscope units. The two gyroscope units are attached on foot and thigh, respectively, and the gyroscope and accelerometer combination unit is located on shank, which is near to ankle. The data recorder can be pocketed by the subject. The principle operation of the gyroscope is the measurement of the Coriolis acceleration, which is generated when a rotational angular velocity is applied to the oscillating piezoelectric bimorph. These inertial sensor can work under low Sensor unit III on the thigh Sensor unit II on the shank Sensor unit I on the foot Fig. 3. Hardware system of the sensor system. A strap system is designed for the binding between the sensor units and human body. The sensor unit is attached to the strap. During walking, the strap is tied around the limb to secure the position of the sensor unit. energy consumption (4.6 ma at 5 V), and are appropriate for ambulatory measurements. The signal from the gyroscopes and accelerometer is amplified and low-pass filtered (cutoff frequency: 25 Hz) to remove electronic noise. The frequencies outside the pass band are filtered out because they are invalid in study of human kinetics. The multi-channel data recorder is specially designed for the wearable sensor system. A micro-computer PIC (16F877A) is used to develop the pocketed data recorder, and sampling data from the inertial sensors can be saved
5 T. Liu et al. / Measurement 42 (2009) in a SRAM. An off-line motion analysis can be performed by feeding data saved in the SRAM to a personal computer through a RS232 communication module or a wireless module. Since gyroscope (ENC-03J), accelerometer-chip (ADXL202) and PIC system are all devices of low energy consumption, the wearable sensor system can be powered using a rechargeable battery of 300 mah (NiMH 30R7H) Calibration of sensor units Complete architecture of a calibration system is showed in Fig. 4(a), and hardware devices of the system mainly include A/D card (Keyence NR-110), a potentiometer, a reference angle finder and a clamp (Fig. 4(b)). The sensor units are calibrated in two states of static and dynamic. The calibration of the accelerometer sensor is carried out during the static state. The accelerometer in sensor unit is subjected to different gravity vectors by rotating a based axis which is connected with a potentiometer. The dynamic calibration is completed to calibrate the gyroscopes and test the accelerometer in a moving condition. In both cases the calibration matrixes are computed using the least squares method. ½C h Š is calibration matrix for the angle position (1), where ½hŠ is the matrix of the imposed quantities, which a b a t, a r, ω p θ 180 a t Clamp Potentiometer ar 90 ω g Reference angle finder 45 0 Sensor unit Table 1 Calibration data of a sensor unit. Angle finder Potentiometer Accelerometer h ( ) p h (V) a t (V) a r (V) in this specific case were obtained when the sensor unit is rotated to different positions on the angle finder plane; ½p h Š is the matrix of the quantities acquired from the potentiometer, in the specific sensor unit positions. Angular position ½h r Š can be calculated using (2), and angular velocity of the sensor unit is obtained through difference computing of the angular positions in serial time. Gravity g subjected to the two sensitive axis (a t and a r ) of the accelerometer is estimated in (3) and (4) ½C h Š¼½hŠ½p h Š T ð½p h Š½p h Š T Þ 1 ð1þ ½h r Š¼½C h Š½p h Š ð2þ A t ¼ gcosðh r Þ ð3þ A r ¼ gsinðh r Þ ð4þ ½C at Š and ½C ar Š are calibration matrixes for the two-axis accelerometer (5) and (6), where ½A t Š and ½A r Š are the matrixes of the imposed quantities, which in this specific case were obtained when the sensor unit is subjected to different g vectors by rotating the sensor unit on the angle finder plane; ½a t Š and ½a r Š are the matrixes of the quantities assessed by the accelerometer in the sensor unit. Eqs. (7) and (8) give summations of subjected gravity g and segment motion acceleration on the two sensitive axes using the output signals of the accelerometer. Table 1 shows data of a sensor unit from a calibration experiment ½C at Š¼½A t Š½a t Š T ð½a t Š½a t Š T Þ 1 ð5þ ½C ar Š¼½A r Š½a r Š T ð½a r Š½a r Š T Þ 1 ð6þ ½A re r Š¼½C arš½a r Š ð7þ ½A re t Š¼½C atš½a t Š ð8þ Fig. 4. (a) Architecture of the equipment for the calibration of the sensor unit. Two-axis accelerometer is used to measure two-directional accelerations of a t and a r, and p h is output signal of the potentiometer which measures imposed rotational quantities and provides reference angular velocity quantities through difference computing. Signal of gyroscope in the sensor unit is defined as x, and its positive direction is anticlockwise. The four signals of p h ; x; a t and a r are sampled into computer through a 12-bit A/D card. (b) Hardware devices with mechanical case and interface for the calibration of the sensor unit. ½C g Š is calibration matrix for gyroscope sensor in the sensor units (9), where ½V g Š and ½p h Š are the matrixes of the quantities, respectively, acquired from the gyroscope and potentiometer in a serial time (t); ½C h Š is calibration matrix for the angle position (1). Angular position ½h r Š can be calculated using (2), and angular velocity of the sensor unit is obtained through difference computing of the angular positions in serial time. Gravity g subjected to the two sensitive axis (a t and a r ) of the accelerometer is estimated in (3) and (4) Z Z Z! T ½C g Š¼½C h Š½p h Š V g dt V g dt V g dt 1 ð9þ
6 982 T. Liu et al. / Measurement 42 (2009) Methods: quantitative gait analysis 3.1. Gait phase detection algorithm In the following discussion, we assume that the subject is viewed from the right lateral side and anticlockwise rotations are considered positive. h f ; h s and h t represent the inclination angles of the foot, shank and thigh with respect to gravity direction, respectively. We also define h f 0 ; h s0 and h t0 as initial (neutral) quantities of the orientation angle. x f ; x s and x t represent the angular velocities of the foot, shank and thigh in the lateral plane, respectively. Finally, e h ; e x and e a represent small threshold values for the detection of close to zero angle displacements, angular velocities and accelerations, respectively. A completed (normal) gait cycle is defined as following: S1: Start of initial contact (end of terminal swing). The hip is flexed, the knee is extended ðh s h t ¼ h s0 h t0 Þ, and the ankle is dorsiflexed to neutral ðh f h s ¼ h f 0 h s0 Þ. The inclinations of the leg segments are obtained by integrating the gyroscopes signal. Sensor condition: x f ¼ e x ; x s ¼ e x and x t ¼ e x. S2: Start of loading response (end of initial contact). Using the heel as a rocker, the knee is flexed for shock absorption (h s h t < h s0 h t0 ; h s > 0andh t > 0). Sensor condition: x f < 0; x s < 0 and x t < 0. S3: Start of mid stance (end of loading response). In this phase, the limb advances over the stationary foot by ankle dorsiflexion (ankle rocker) while the knee and hip extend ðh s h t ¼ e h Þ. Sensor condition: x f ¼ e x ; x s < 0 and x t < 0. S4: Start of terminal stance (end of mid stance). The terminal stance begins with heel rise and continues until the other foot strikes the ground, in which the heel rise and the limb advance over the forefoot rocker (h s h t ¼ h s0 h t0 ; h f < 0; h s < 0 and h t < 0Þ. Sensor condition: x f < 0; x s < 0 and x t < 0. S5: Start of pre-swing (end of terminal stance). The limb responds with increased ankle plantar flexion ðh f < 0Þ, greater knee flexion ðh s h t < 0Þ and loss of hip extension. Sensor condition: x f < 0; x s < 0andx t < 0. S6: Start of initial swing (end of pre-swing). In this phase, the foot is lifted and limb advanced by hip flexion and increased knee flexion ðh s h t < 0Þ. Sensor condition: x f > 0; x s > 0 and x t > 0. S7: Start of mid swing (end of initial swing). The knee is allowed to extend in response to gravity while the ankle continues dorsiflexion to neural (h f h s < 0; h t > 0 and h s < e h ). Sensor condition: x f > 0; x s > 0 and x t > 0. S8: Start of terminal swing (end of mid swing). Limb advancement is completed as the leg (shank) moves ahead of the thigh. In this phase the limb advancement is completed by knee extension, and the hip maintains its earlier flexion ðh f h s ¼ h f 0 h s0 Þ, and the ankle remains dorsiflexed to neural. Sensor condition: x f x s ¼ e x and x t > 0. In this paper, the motion analysis system with intelligent calibration for leg segment quantitative leg-motion analysis is developed. According above quantitative assessment of the eight gait phases, if the leg segments orientations (h f ; h s and h t ) cannot be accurately obtained and combined with the signals of the sensor units (x f ; x s and x t ), it is almost impossible that all the gait phases are effectively detected Quantitative gait analysis The loop frequency of the phase record is 100 Hz, i.e., equal to the sensors sampling frequency, and the number of sampling time point is counted in an integer value i (i = 1,2,3,...). The orientation of leg segment ðhðiþþ can be calculated by integration of the angular velocity ðxðiþþ of leg segment ((9) and (10)), which is directly measured using the wearable sensor unit. The inclination of shank and thigh is set to zero in the initial period, while the inclination of foot is set to 90 at start. However, the gyroscope in the sensor unit is a kind of inertial sensor that is affected by drift errors when it is worn on human body, so the integral calculation in (9) may produce cumulated errors in a multi-step walking motion analysis hðiþ ¼hði 1Þþðxði 1ÞþxðiÞÞDt=2 ð9þ where hð0þ ¼h 0 ; i ¼ 1; 2; 3... ð10þ We define the gait cycle (walking gait cycle number k =1,2,...) as the period from one stance phase of the foot to the next stance phase of one foot. In every walking cycle, the time points of transition from loading response phase to mid stance phase, and transition from pre-swing to initial swing phase are defined as T 41 ðkþ; T 42 ðkþ; T 43 ðkþ and T 44 ðkþ, respectively. Based on a pre-analysis of gait phase, the human motion analysis is implemented by calculating body segments angular displacements using inertial sensors of gyroscopes and accelerometers. As shown in Fig. 5, we can primarily detect the mid stance phase just using gyroscope signals and raw integration results of gyroscope signals from the three sensor units (x t < 0; x f ¼ e x ; x s < 0 and h s < 0). Moreover, we find that the rotational angular velocities of the shank and thigh are very small in later interval of this phase, because ankle is in state of dorsiflexion, and shank rotational velocity is limited. Therefore, the accelerometer can be used for inclination measurement with respect to gravity acceleration, when shank s sagittal direction A r (11) and A t (12) are mainly affected by the gravity acceleration s projection. Hence, we can make cycle calibration by measuring initial angular orientation of the attached segment (shank) using (13), and foot orientation ðh m f ¼ 0Þ and thigh orientation ðh m t ¼ h m s Þ are the initial calibration quantities for calculation of foot and thigh orientation. Integral calculations are performed in every gait cycle, which can decrease the cumulated errors in the longtime walking experiments A r ¼ gsinðh m s ÞþDðxm s Þ2 ð11þ A t ¼ gcosðh m s ÞþD _x m s ð12þ h m s ¼ arctanða r =A t Þ ð13þ However, some subjects (e.g., paralytic patient) the heel may never contact the ground, and the proposed direct inference algorithm cannot be used for cycle recalibration
7 T. Liu et al. / Measurement 42 (2009) Quadriceps From early interval to late interval Femur Knee Tibia Soleus, gastrocnemius D Sensor unit II Ankle rocker Foot Fig. 5. Mid stance phase including early interval and late interval. The orientation calibration is implemented in late interval of mid stand. Early interval has body over mid foot with climb vertical, ankle neutral and foot flat, in which quadriceps and soleus muscles are in activity. Later interval has body over forefoot with continued heel contact, while ankle is in state of dorsiflexion which limit shank rotational velocity. A small distance between sensor unit II and ankle rocker is denoted using D (it is about 50 mm). Moreover in later interval, soleus and gastrocnemius are only extensor muscles around tibia, which produces least vibration effect on the accelerometer. to decrease integration error. A linear regression method was developed to calculate drift error coming from digital integration, in which we supposed the error increase in linear function. The summary error ðh e ¼ h i h m Þ is obtained from single walking test in which subjects are requested to walk along a straight leading line, in which we let h i be direct integration results by (9), and h m be reference static inclination angle measured using accelerometer by (13). Error estimation function ðh e ðiþþ is given as following equation based to linear regression h e ðiþ ¼Dt i ðh i h m Þ=t; i ¼ 1; 2; 3;...; t ð14þ h c ðiþ ¼hðiÞ h e ðiþ ð15þ where Dt is sampling time and h c ðiþ was defined as estimated angle with error correction. A group of example figures including hðiþ and h e ðiþ for foot angle estimation is shown in Fig. 6. Drift error was significantly reduced from the simplified error estimation method; in the next step, the results of leg segment orientation were compared with measurements of a commercial motion analysis system based to high-speed cameras The optical motion analysis system To validate the sensor system performance we have compared the quantitative results of the sensor system with the measurements obtained with a commercial optical motion analysis system Hi-DCam (NAC Image Technology, Japan). Hi-DCam tracked and measured the three-dimensional (3D) trajectories of retro-reflective markers placed on the subject s body, as shown in Fig. 7. Two high-speed cameras with sampling frequency Fig. 6. Example figures of foot segment orientation estimated by eliminating linear drift error. 50 Hz are used to track the marker positions with accuracy of 1 mm Performance analysis of the sensor system Two criteria are used to evaluate the similarity between results of the sensor system and results of the optical motion analysis system. 1. The motion analysis results of the two systems should be identical in a time domain and therefore the correlation coefficient should approach one. 2. The motion analysis results of the two systems should be quantitatively identical, and therefore the root mean squared error (RMSE) should approach zero. The correlation coefficient is calculated to compare motion analysis results of the two sensor systems. If the Thigh marker Knee marker Ankle marker Heel marker Toe marker Fig. 7. Positions of the retro-reflective markers.
8 984 T. Liu et al. / Measurement 42 (2009) Fig. 8. Signals of the gyroscopes worn on a subject s limb. Fig. 9. Estimation results of leg segments rotational angles. correlation coefficient has a value closed to +1, then there is a linear relationship between these two results in the time domain. Correlation coefficient (R) is defined as: ðn P FF r P F P F r Þ R ¼ rffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi n P F 2 ð P FÞ 2 n P F 2 r ð P F r Þ 2 ð16þ where F is the results obtained from the developed sensor system, F r is the results from the reference optical motion analysis system, and the n is the number of the sample data. Moreover, the root mean squared error (RMSE) is used to compare the closeness in amplitude of the two system s measurement results. The percent error (PE) was calculated as the ratio between the RMSE errors to the average peak-to-peak amplitude of the optical analysis system s measurements s ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi 1 X RMSE ¼ ðf Fr Þ 2 ð17þ n 4. Experimental study The experiment of the sensory system for leg-motion analysis is implemented in the following three steps. First, the sensor devices are worn on the subject s leg to measure 2D motion of the foot, shank and thigh, and the sensors data are saved in the pocketed data recorder. Second, when the human motion record is finished, the data in the data recorder will be fed into personal computer through serial port (RS232), then leg-motion data is prepared for the offline motion analysis computing. Finally, the leg-motion analysis is performed to estimate the leg segments angular orientations Drift effect As shown in Fig. 8 and Fig. 9, an off-line analysis was made to analyze the leg segments motion during walking, when the subject walked with a stride length about 0.8 m, a gait cycle time about 1.2 s. The experiments data were processed using MATLAB, in which a direct integral calculation was designed to estimate orientations of the three leg segments. We have completed the motion analysis experiments on 10 subjects (average age, 21; average height, 1.7 m). To test drift error from the gyroscope worn on human body, we have compared the quantitative results of the sensor system using direct integral calculation with the measurements obtained with a commercial optical motion analysis system. As shown in Table 2, the maximum value of RMSE the orientation error during walking experiments Table 2 RMSE of orientation drift from integral calculation. Foot (RMSE) Shank (RMSE) Thigh (RMSE) Stride 1 Stride 2 Stride 3 Stride 1 Stride 2 Stride 3 Stride 1 Stride 2 Stride 3 Subject Subject Subject Subject Subject Subject Subject Subject Subject Subject
9 T. Liu et al. / Measurement 42 (2009) Intelligent calibration for reducing drift Fig. 10. Average orientation drift error (RMSE value) using direct integral calculation. In the serial three strides the drift of the three segments (foot, shank and thigh) continuously increases when using direct integral calculation from gyroscope signals. is 16.6 because of effects of drift. In the serial three strides, the drift of the three segments (foot, shank and thigh) continuously increase when using direct integral calculation from gyroscope signals (Fig. 10). The mid stance phase can be detected just using gyroscope signals and raw integration results of gyroscope signals from the three sensor units (x t < 0; x f ¼ e x ; x s < 0 and h s < 0). Moreover, we find that the rotational angular velocities of the shank and thigh are very small in later interval of this phase, because ankle is in state of dorsiflexion, and shank rotational velocity is limited. Therefore, the accelerometer can be used for inclination measurement with respect to gravity acceleration, when shank s sagittal direction A r (11) and A t (12) are mainly affected by the gravity acceleration s projection. Fig. 11 shows a subject walking experiment on period calibration for reducing drifts. In each mid stance phase of the four strides, the angle signals from accelerometer were used as initial value of integral calculation instead of the value from integral signal of the gyroscope (Table 3). Calibration experiments were finished on a group of subjects using the signals of the wearable sensor system and the optical motion analysis system. As shown in Fig. 12, the shank angle of a subject was derived from our motion analysis system in time domain. The drift Fig. 11. Period calibration by fusing signals of gyroscopes and accelerometers. (a) Late interval of mid stance in a gait cycle. Mid stance phase can be detected using gyroscopes on low limb: x t < 0; x f ¼ e x; x s < 0 and h s < 0. (b) Signals of accelerometer attached on shank during human walking. In the whole gait cycle, the acceleration measurements include projections of the sum of gravity acceleration and the attached segment motion. The accelerometer can work as a orientation meter in the late interval of mid stance, because the shank is moving with small rotational velocity and acceleration, and the accelerometer is near from rocker (the distance D between accelerometer and ankle joint is about 50 mm). (c) Angular orientations from gyroscope and accelerometer. The intelligent calibrations are implemented through resetting initial value in the integral calculation of gyroscope signal, in which the orientations from accelerometer is used to provide the integral initial value (13).
10 986 T. Liu et al. / Measurement 42 (2009) Table 3 RMSE of orientation drift from integral calculation. Stride Time (s) h s ( ) h m s ( ) h s : Shank angle calculated from signal of gyroscope using integral computing (9). : Shank angle from signal of accelerometer using (13). h m s Fig. 14. Average orientation error (RMSE value) using intelligent calibration. In the serial three strides the drift of the three segments (foot, shank and thigh) continuously increases when using direct integral calculation from gyroscope signals. The drift errors are never accumulated with increasing strides, when the calibration is implemented by fusing data of gyroscopes and accelerometers. Fig. 12. Period calibration by fusing signals of gyroscopes and accelerometers. errors are never accumulated with increasing strides, when the calibration was implemented by fusing data of gyroscopes and accelerometers. A set of example comparison figures from verification experiments on segmental angular displacements measured by wearable sensor systems and optical motion analysis systems (Hi-DCam) is given in Fig. 13, which demonstrate the two systems measurement results have high consistence. Moreover, Fig. 14 provides a statistical result about the validity of the intelligent calibration for decreasing drift, and experiments were completed on the ten healthy subjects. The average RMSE was not over 5.0 (the thigh angle orientation) when the calibration is implemented. Correlation coefficient (R) was not under 0.9 for the segment angles from the wearable sensor system and the results from the optical motion analysis system. 5. Discussions and conclusions Quantitative human motion analysis was implemented using a developed wearable sensor system with intelligent calibration. The results from the sensor system showed a high correlation to the results from the optical motion analysis system in the multi-step walking experiments, Fig. 13. Segmental angular displacements measured by wearable sensor systems (solid line) and Hi-DCam camera systems (dashed line). (a) Foot angular displacements. (b) Shank angular displacements. (c) Thigh angular displacements.
11 T. Liu et al. / Measurement 42 (2009) which proved the validity of the intelligent calibration method for decreasing drift errors. Pappas et al. [19] described a gait phase detection system which can be used in gait analysis applications and to control gait cycle of a neuroprosthesis for walking, but this system was only designed to detect in real time the following gait phases: stance, heel-off, swing, and heelstrike. This kind of gait phase detection often failed to accommodate the gait deviations of patients impaired by paralysis or arthritis whose heel may never contact the ground or do so much later in a gait cycle. In this paper, a normal walking gait cycle is divided into eight gait phases: initial contact, loading response, mid stance, terminal stance, pre-swing, initial swing, mid swing and terminal swing from the generic terminology developed by the Rancho Los Amigos gait analysis committee. We detected the eight gait phases using leg segments orientation angles and the signals of gyroscopes. The muscular tensions are very complex during walking, and the electromyogram (EMG) is a common method for this study. In next step of this study, we want to develop a wearable sensor system for estimating muscular tensions instead of EMG. Analysis of human walking pattern by the eight gait phases more directly identifies the functional significance (muscular tensions) of the different motions accruing at the individual joints and segments. For example, in mid stance phase including early interval and late interval, the early interval has body over mid foot, in which quadriceps and soleus muscles are in activity; later interval has body over forefoot, in which soleus and gastrocnemius are only extensor muscles around tibia. We can combine the developed wearable human motion analysis sensor system with a reaction force sensor worn under foot to estimate muscular tensions. The gait phase division will improve the precision of this method by providing constrain condition about the functional muscles for an optimum analysis [35,36]. Moreover, in the study of robotics, this wearable sensor system is applied for realtime control of a humanoid robot which may walk in the same phase as human walking. References [1] I.A. Karaulova, P.M. Hall, A.D. Marshall, Tracking people in three dimensions using a hierarchical model, Image and Vision Computing 20 (2002) [2] Y. Inoue, T. Matsuda, K. Shibata, Estimation of vertical reaction force and ankle joint moment by using plantar pressure sensor, in: JSME Symposium on Human Dynamics, 2003, pp [3] W.Y. Wong, M.S. Wong, K.H. Lo, Clinical applications of sensors for human posture and movement analysis: a review, Prosthetics and Orthotics International 31 (2007) [4] H. Zheng, N.D. Black, N.D. Harris, Position-sensing technologies for movement analysis in stroke rehabilitation, Medical and Biological Engineering and Computing 43 (4) (2005) [5] K. Turcot, R. Aissaoui, K. Boivin, M. Pelletier, N. Hagemeister, J.A. De Guise, New accelerometric method to discriminate between asymptomatic subjects and patients with medial knee osteoarthritis during 3-D gait, IEEE Transactions on Biomedical Engineering 55 (4) (2008) [6] A. Zijlstra, J.H.M. Goosen, C.C.P.M. Verheyen, W. Zijlstra, A body-fixedsensor based analysis of compensatory trunk movements during unconstrained walking, Gait and Posture 27 (1) (2008) [7] A.K. Bourke, G.M. Lyons, A threshold-based fall-detection algorithm using a bi-axial gyroscope sensor, Medical Engineering and Physics 30 (1) (2008) [8] J. Favre, F. Luthi, B.M. Jolles, O. Siegrist, B. Najafi, K. Aminian, A new ambulatory system for comparative evaluation of the threedimensional knee kinematics, applied to anterior cruciate ligament injuries, Knee Surgery, Sports Traumatology, Arthroscopy 14 (7) (2006) [9] K. Aminian, B. Najafi, Capturing human motion using body-fixed sensors: outdoor measurement and clinical applications, Computer Animation and Virtual Worlds 15 (2) (2004) [10] J.J. Kavanagh, H.B. Menz, Accelerometry: a technique for quantifying movement patterns during walking, Gait and Posture 28 (1) (2008) [11] A.M. Sabatini, C. Martelloni, S. Scapellato, F. Cavallo, Assessment of walking features from foot inertial sensing, IEEE Transactions on Biomedical Engineering 52 (3) (2005) [12] K. Aminian, B. Najafi, C. Bula, P.-F. Leyvraz, Ph. Robert, Spatiotemporal parameters of gait measured by an ambulatory system using miniature gyroscopes, Journal of Biomechanics 35 (5) (2002) [13] B. Coley, B. Najafi, A. Paraschiv-Ionescu, K. Aminian, Stair climbing detection during daily physical activity using a miniature gyroscope, Gait and Posture 22 (4) (2005) [14] H.-Y. Lau, K.-Y. Tong, H. Zhu, Support vector machine for classification of walking conditions using miniature kinematic sensors, Medical and Biological Engineering and Computing 46 (6) (2008) [15] B. Najafi, K. Aminian, F. Loew, Y. Blanc, P.A. Robert, Measurement of stand-sit and sit-stand transitions using a miniature gyroscope and its application in fall risk evaluation in the elderly, IEEE Transactions on Biomedical Engineering 49 (8) (2002) [16] K. Aminian, Ph. Robert, E.E. Buchser, B. Rutschmann, D. Hayoz, M. Depairon, Physical activity monitoring based on accelerometry: validation and comparison with video observation, Medical and Biological Engineering and Computing 37 (3) (1999) [17] H. Lau, K. Tong, The reliability of using accelerometer and gyroscope for gait event identification on persons with dropped foot, Gait and Posture 27 (2) (2008) [18] I.P.I. Pappas, T. Keller, S. Mangold, M.R. Popovic, V. Dietz, M. Morari, A reliable gyroscope-based gait-phase detection sensor embedded in a shoe insole, IEEE Sensors Journal 4 (2) (2004) [19] I.P.I. Pappas, M.R. Popovic, T. Keller, V. Dietz, M. Morari, A reliable gait phase detection system, IEEE Transactions on Neural Systems and Rehabilitation Engineering 9 (2) (2001) [20] J.M. Jasiewicz, J.H.J. Allum, J.W. Middleton, A. Barriskill, P. Condie, B. Purcell, R.C.T. Li, Gait event detection using linear accelerometers or angular velocity transducers in able-bodied and spinal-cord injured individuals, Gait and Posture 24 (4) (2006) [21] Available from: < [22] H. Dejnabadi, B.M. Jolles, K. Aminian, A new approach to accurate measurement of uniaxial joint angles based on a combination of accelerometers and gyroscopes, IEEE Transactions on Biomedical Engineering 52 (8) (2005) [23] R. Williamson, B.J. Andrews, Detecting absolute human knee angle and angular velocity using accelerometers and rate gyroscopes, Medical and Biological Engineering and Computing 39 (3) (2001) [24] J. Favre, B.M. Jolles, R. Aissaoui, K. Aminian, Ambulatory measurement of 3D knee joint angle, Journal of Biomechanics 41 (5) (2008) [25] R. Zheng, T. Liu, Y. Inoue, K. Shibata, K. Liu, Kinetics analysis of ankle, knee and hip joints using a wearable sensor system, Journal of Biomechanical Science and Engineering 3 (3) (2008) [26] A.M. Sabatini, Quaternion-based strap-down integration method for applications of inertial sensing to gait analysis, Medical and Biological Engineering and Computing 43 (1) (2005) [27] H.J. Luinge, P.H. Veltink, Measuring orientation of human body segments using miniature gyroscopes and accelerometers, Medical and Biological Engineering and Computing 43 (2) (2005) [28] H.J. Luinge, P.H. Veltink, C.T.M. Baten, Ambulatory measurement of arm orientation, Journal of Biomechanics 40 (1) (2007) [29] R.E. Mayagoitia, A.V. Nene, P.H. Veltink, Accelerometer and rate gyroscope measurement of kinematics: an inexpensive alternative to optical motion analysis systems, Journal of Biomechanics 35 (4) (2002) [30] H. Dejnabadi, B.M. Jolles, E. Casanova, P. Fua, K. Aminian, Estimation and visualization of sagittal kinematics of lower limbs orientation using body-fixed sensors, IEEE Transactions on Biomedical Engineering 53 (7) (2006)
12 988 T. Liu et al. / Measurement 42 (2009) [31] J.Y. Goulermas, D. Howard, C.J. Nester, R.K. Jones, L. Ren, Regression techniques for the prediction of lower limb kinematics, Journal of Biomechanical Engineering 127 (6) (2005) [32] A. Findlow, J.Y. Goulermas, C. Nester, D. Howard, L.P.J. Kenney, Predicting lower limb joint kinematics using wearable motion sensors, Gait and Posture 28 (1) (2008) [33] Pathokinesiology Department, Physical Therapy Department: Observational Gait Analysis Handbook, CA, The Professional Staff Association of Rancho Los Amigos Medical Center, [34] J. Parry, Gait Analysis Normal and Pathological Function, Slack Incorporated, [35] A. Pedotti, V.V. Krishnan, L. Stark, Optimization of muscle-force sequencing in human locomotion, Mathematical Biosciences 38 (1978) [36] Y. Ehara, M. Beppu, S. Nomura, Y. Kunimi, Estimation of energy consumption during level walking, Biomechanisms 10 (1990)
Development of Wearable Sensor Combinations for Human Lower Extremity Motion Analysis
 Proceedings of the 2006 IEEE International Conference on Robotics and Automation Orlando, Florida - May 2006 Development of Wearable Sensor Combinations for Human Lower Extremity Motion Analysis Tao Liu,
Proceedings of the 2006 IEEE International Conference on Robotics and Automation Orlando, Florida - May 2006 Development of Wearable Sensor Combinations for Human Lower Extremity Motion Analysis Tao Liu,
gait phases analysis. In the study by S. K. Ng and H. J.
 Proceedings 2005 IEEE International Symposium on Computational Intelligence in Robotics and Automation June 27-30, 2005, Espoo, Finland A Wearable Inertial Sensor System for Human Motion Analysis Tao Liu,
Proceedings 2005 IEEE International Symposium on Computational Intelligence in Robotics and Automation June 27-30, 2005, Espoo, Finland A Wearable Inertial Sensor System for Human Motion Analysis Tao Liu,
An investigation of kinematic and kinetic variables for the description of prosthetic gait using the ENOCH system
 An investigation of kinematic and kinetic variables for the description of prosthetic gait using the ENOCH system K. OBERG and H. LANSHAMMAR* Amputee Training and Research Unit, University Hospital, Fack,
An investigation of kinematic and kinetic variables for the description of prosthetic gait using the ENOCH system K. OBERG and H. LANSHAMMAR* Amputee Training and Research Unit, University Hospital, Fack,
Dynamic analysis and motion measurement of ski turns using inertial and force sensors
 Available online at www.sciencedirect.com Procedia Engineering 6 ( 213 ) 355 36 6th Asia-Pacific Conference on Sports Technology Dynamic analysis and motion measurement of ski turns using inertial and
Available online at www.sciencedirect.com Procedia Engineering 6 ( 213 ) 355 36 6th Asia-Pacific Conference on Sports Technology Dynamic analysis and motion measurement of ski turns using inertial and
Biomechanics and Models of Locomotion
 Physics-Based Models for People Tracking: Biomechanics and Models of Locomotion Marcus Brubaker 1 Leonid Sigal 1,2 David J Fleet 1 1 University of Toronto 2 Disney Research, Pittsburgh Biomechanics Biomechanics
Physics-Based Models for People Tracking: Biomechanics and Models of Locomotion Marcus Brubaker 1 Leonid Sigal 1,2 David J Fleet 1 1 University of Toronto 2 Disney Research, Pittsburgh Biomechanics Biomechanics
 Kochi University of Technology Aca Study on Dynamic Analysis and Wea Title stem for Golf Swing Author(s) LI, Zhiwei Citation 高知工科大学, 博士論文. Date of 2015-03 issue URL http://hdl.handle.net/10173/1281 Rights
Kochi University of Technology Aca Study on Dynamic Analysis and Wea Title stem for Golf Swing Author(s) LI, Zhiwei Citation 高知工科大学, 博士論文. Date of 2015-03 issue URL http://hdl.handle.net/10173/1281 Rights
Takashi Watanabe, Hiroki Saito, Eri Koike, and Kazuki Nitta. 1. Introduction
 Computational Intelligence and Neuroscience Volume 211, Article ID 975193, 12 pages doi:1.1155/211/975193 Research Article A Preliminary Test of Measurement of Joint Angles and Stride Length with Wireless
Computational Intelligence and Neuroscience Volume 211, Article ID 975193, 12 pages doi:1.1155/211/975193 Research Article A Preliminary Test of Measurement of Joint Angles and Stride Length with Wireless
CHAPTER IV FINITE ELEMENT ANALYSIS OF THE KNEE JOINT WITHOUT A MEDICAL IMPLANT
 39 CHAPTER IV FINITE ELEMENT ANALYSIS OF THE KNEE JOINT WITHOUT A MEDICAL IMPLANT 4.1 Modeling in Biomechanics The human body, apart of all its other functions is a mechanical mechanism and a structure,
39 CHAPTER IV FINITE ELEMENT ANALYSIS OF THE KNEE JOINT WITHOUT A MEDICAL IMPLANT 4.1 Modeling in Biomechanics The human body, apart of all its other functions is a mechanical mechanism and a structure,
NIH Public Access Author Manuscript Gait Posture. Author manuscript; available in PMC 2009 May 1.
 NIH Public Access Author Manuscript Published in final edited form as: Gait Posture. 2008 May ; 27(4): 710 714. Two simple methods for determining gait events during treadmill and overground walking using
NIH Public Access Author Manuscript Published in final edited form as: Gait Posture. 2008 May ; 27(4): 710 714. Two simple methods for determining gait events during treadmill and overground walking using
Walking Speed Estimation Using a Shank-Mounted Inertial Measurement Unit
 Walking Speed Estimation Using a Shank-Mounted Inertial Measurement Unit Q. Li,a,b, M. Young c, V. Naing c, J.M. Donelan c a Department of Mechanical and Materials Engineering, Queen s University, Kingston,
Walking Speed Estimation Using a Shank-Mounted Inertial Measurement Unit Q. Li,a,b, M. Young c, V. Naing c, J.M. Donelan c a Department of Mechanical and Materials Engineering, Queen s University, Kingston,
Analysis of stroke technique using acceleration sensor IC in freestyle swimming
 Analysis of stroke technique using acceleration sensor IC in freestyle swimming Y. Ohgi, M. Yasumura Faculty of Environmental Information, Keio Univ., Japan H. Ichikawa Doctoral Prog. of Health and Sport
Analysis of stroke technique using acceleration sensor IC in freestyle swimming Y. Ohgi, M. Yasumura Faculty of Environmental Information, Keio Univ., Japan H. Ichikawa Doctoral Prog. of Health and Sport
Transformation of nonfunctional spinal circuits into functional states after the loss of brain input
 Transformation of nonfunctional spinal circuits into functional states after the loss of brain input G. Courtine, Y. P. Gerasimenko, R. van den Brand, A. Yew, P. Musienko, H. Zhong, B. Song, Y. Ao, R.
Transformation of nonfunctional spinal circuits into functional states after the loss of brain input G. Courtine, Y. P. Gerasimenko, R. van den Brand, A. Yew, P. Musienko, H. Zhong, B. Song, Y. Ao, R.
Supplementary Figure S1
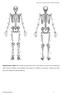 Supplementary Figure S1: Anterior and posterior views of the marker set used in the running gait trials. Forty-six markers were attached to the subject (15 markers on each leg, 4 markers on each arm, and
Supplementary Figure S1: Anterior and posterior views of the marker set used in the running gait trials. Forty-six markers were attached to the subject (15 markers on each leg, 4 markers on each arm, and
Improving pedestrian dynamics modelling using fuzzy logic
 Improving pedestrian dynamics modelling using fuzzy logic Phillip Tomé 1, François Bonzon 1, Bertrand Merminod 1, and Kamiar Aminian 2 1 EPFL Geodetic Engineering Lab (TOPO) Station 18 1015 Lausanne Switzerland
Improving pedestrian dynamics modelling using fuzzy logic Phillip Tomé 1, François Bonzon 1, Bertrand Merminod 1, and Kamiar Aminian 2 1 EPFL Geodetic Engineering Lab (TOPO) Station 18 1015 Lausanne Switzerland
Gait. Kinesiology RHS 341 Lecture 12 Dr. Einas Al-Eisa
 Gait Kinesiology RHS 341 Lecture 12 Dr. Einas Al-Eisa Definitions Locomotion = the act of moving from one place to the other Gait = the manner of walking Definitions Walking = a smooth, highly coordinated,
Gait Kinesiology RHS 341 Lecture 12 Dr. Einas Al-Eisa Definitions Locomotion = the act of moving from one place to the other Gait = the manner of walking Definitions Walking = a smooth, highly coordinated,
APPLICATION OF THREE DIMENSIONAL ACCELEROMETRY TO HUMAN MOTION ANALYSIS
 APPLICATION OF THREE DIMENSIONAL ACCELEROMETRY TO HUMAN MOTION ANALYSIS INTRODUCTION Ken'ichi Egawa, T. Tsuboi, T. Satoh, and M. Miyazaki Graduate School of Human Sciences, Waseda University Three dimensional
APPLICATION OF THREE DIMENSIONAL ACCELEROMETRY TO HUMAN MOTION ANALYSIS INTRODUCTION Ken'ichi Egawa, T. Tsuboi, T. Satoh, and M. Miyazaki Graduate School of Human Sciences, Waseda University Three dimensional
Artifacts Due to Filtering Mismatch in Drop Landing Moment Data
 Camenga et al. UW-L Journal of Undergraduate Research XVI (213) Artifacts Due to Filtering Mismatch in Drop Landing Moment Data Elizabeth T. Camenga, Casey J. Rutten, Brendan D. Gould, Jillian T. Asmus,
Camenga et al. UW-L Journal of Undergraduate Research XVI (213) Artifacts Due to Filtering Mismatch in Drop Landing Moment Data Elizabeth T. Camenga, Casey J. Rutten, Brendan D. Gould, Jillian T. Asmus,
Journal of Biomechanics
 Journal of Biomechanics 43 (2010) 3138 3143 Contents lists available at ScienceDirect Journal of Biomechanics journal homepage: www.elsevier.com/locate/jbiomech www.jbiomech.com Ambulatory estimation of
Journal of Biomechanics 43 (2010) 3138 3143 Contents lists available at ScienceDirect Journal of Biomechanics journal homepage: www.elsevier.com/locate/jbiomech www.jbiomech.com Ambulatory estimation of
Using GPOPS-II to optimize sum of squared torques of a double pendulum as a prosthesis leg. Abstract
 Using GPOPS-II to optimize sum of squared torques of a double pendulum as a prosthesis leg Abstract Milad Zarei MCE 593 Prosthesis Design & Control A two-dimensional, two links pendulum is developed to
Using GPOPS-II to optimize sum of squared torques of a double pendulum as a prosthesis leg Abstract Milad Zarei MCE 593 Prosthesis Design & Control A two-dimensional, two links pendulum is developed to
Dynamically stepping over large obstacle utilizing PSO optimization in the B4LC system
 1 Dynamically stepping over large obstacle utilizing PSO optimization in the B4LC system QI LIU, JIE ZHAO, KARSTEN BERNS Robotics Research Lab, University of Kaiserslautern, Kaiserslautern, 67655, Germany
1 Dynamically stepping over large obstacle utilizing PSO optimization in the B4LC system QI LIU, JIE ZHAO, KARSTEN BERNS Robotics Research Lab, University of Kaiserslautern, Kaiserslautern, 67655, Germany
WALKING MOTION ANALYSIS USING SMALL ACCELERATION SENSORS
 WALKING MOTION ANALYSIS USING SMALL ACCELERATION SENSORS Teruaki Ito Institute of Technology and Science University of Tokushima Tokushima, Japan e-mail: ito@me.tokushima-u.ac.jp Abstract Human walking
WALKING MOTION ANALYSIS USING SMALL ACCELERATION SENSORS Teruaki Ito Institute of Technology and Science University of Tokushima Tokushima, Japan e-mail: ito@me.tokushima-u.ac.jp Abstract Human walking
Stride October 20, 2017
 Preliminary Design Review Stride October 20, 2017 Advisor: ProfessorTessier Hollot 1 Advisor : Professor Group Members Richie Hartnett CSE Jarred Penney EE Advisor Prof. Tessier Joe Menzie CSE Jack Higgins
Preliminary Design Review Stride October 20, 2017 Advisor: ProfessorTessier Hollot 1 Advisor : Professor Group Members Richie Hartnett CSE Jarred Penney EE Advisor Prof. Tessier Joe Menzie CSE Jack Higgins
Gait analysis for the development of the biped robot foot structure
 Preprints of the 9th World Congress The International Federation of Automatic Control Cape Town, South Africa. August 4-9, 4 Gait analysis for the development of the biped robot foot structure Yusuke OGAWA
Preprints of the 9th World Congress The International Federation of Automatic Control Cape Town, South Africa. August 4-9, 4 Gait analysis for the development of the biped robot foot structure Yusuke OGAWA
REPRESENTATION OF HUMAN GAIT TRAJECTORY THROUGH TEMPOROSPATIAL IMAGE MODELLING
 REPRESENTATION OF HUMAN GAIT TRAJECTORY THROUGH TEMPOROSPATIAL IMAGE MODELLING Md. Akhtaruzzaman, Amir A. Shafie and Md. Raisuddin Khan Department of Mechatronics Engineering, Kulliyyah of Engineering,
REPRESENTATION OF HUMAN GAIT TRAJECTORY THROUGH TEMPOROSPATIAL IMAGE MODELLING Md. Akhtaruzzaman, Amir A. Shafie and Md. Raisuddin Khan Department of Mechatronics Engineering, Kulliyyah of Engineering,
Toward a Human-like Biped Robot with Compliant Legs
 Book Title Book Editors IOS Press, 2003 1 Toward a Human-like Biped Robot with Compliant Legs Fumiya Iida a,b,1, Yohei Minekawa a Juergen Rummel a and Andre Seyfarth a a Locomotion Laboratory, University
Book Title Book Editors IOS Press, 2003 1 Toward a Human-like Biped Robot with Compliant Legs Fumiya Iida a,b,1, Yohei Minekawa a Juergen Rummel a and Andre Seyfarth a a Locomotion Laboratory, University
Body Stabilization of PDW toward Humanoid Walking
 Body Stabilization of PDW toward Humanoid Walking Masaki Haruna, Masaki Ogino, Koh Hosoda, Minoru Asada Dept. of Adaptive Machine Systems, Osaka University, Suita, Osaka, 565-0871, Japan ABSTRACT Passive
Body Stabilization of PDW toward Humanoid Walking Masaki Haruna, Masaki Ogino, Koh Hosoda, Minoru Asada Dept. of Adaptive Machine Systems, Osaka University, Suita, Osaka, 565-0871, Japan ABSTRACT Passive
by Michael Young Human Performance Consulting
 by Michael Young Human Performance Consulting The high performance division of USATF commissioned research to determine what variables were most critical to success in the shot put The objective of the
by Michael Young Human Performance Consulting The high performance division of USATF commissioned research to determine what variables were most critical to success in the shot put The objective of the
In memory of Dr. Kevin P. Granata, my graduate advisor, who was killed protecting others on the morning of April 16, 2007.
 Acknowledgement In memory of Dr. Kevin P. Granata, my graduate advisor, who was killed protecting others on the morning of April 16, 2007. There are many others without whom I could not have completed
Acknowledgement In memory of Dr. Kevin P. Granata, my graduate advisor, who was killed protecting others on the morning of April 16, 2007. There are many others without whom I could not have completed
Inertial compensation for belt acceleration in an instrumented treadmill
 Inertial compensation for belt acceleration in an instrumented treadmill Sandra K. Hnat, Antonie J. van den Bogert Department of Mechanical Engineering, Cleveland State University Cleveland, OH 44115,
Inertial compensation for belt acceleration in an instrumented treadmill Sandra K. Hnat, Antonie J. van den Bogert Department of Mechanical Engineering, Cleveland State University Cleveland, OH 44115,
Computer Aided Drafting, Design and Manufacturing Volume 26, Number 2, June 2016, Page 53. The design of exoskeleton lower limbs rehabilitation robot
 Computer Aided Drafting, Design and Manufacturing Volume 26, Number 2, June 2016, Page 53 CADDM The design of exoskeleton lower limbs rehabilitation robot Zhao Xiayun 1, Wang Zhengxing 2, Liu Zhengyu 1,3,
Computer Aided Drafting, Design and Manufacturing Volume 26, Number 2, June 2016, Page 53 CADDM The design of exoskeleton lower limbs rehabilitation robot Zhao Xiayun 1, Wang Zhengxing 2, Liu Zhengyu 1,3,
Mobility Lab provides sensitive, valid and reliable outcome measures.
 Mobility Lab provides sensitive, valid and reliable outcome measures. ith hundreds of universities and hospitals using this system worldwide, Mobility Lab is the most trusted wearable gait and balance
Mobility Lab provides sensitive, valid and reliable outcome measures. ith hundreds of universities and hospitals using this system worldwide, Mobility Lab is the most trusted wearable gait and balance
Open Research Online The Open University s repository of research publications and other research outputs
 Open Research Online The Open University s repository of research publications and other research outputs Developing an intelligent table tennis umpiring system Conference or Workshop Item How to cite:
Open Research Online The Open University s repository of research publications and other research outputs Developing an intelligent table tennis umpiring system Conference or Workshop Item How to cite:
Jogging and Walking Analysis Using Wearable Sensors *
 Engineering, 2013, 5, 20-24 doi:10.4236/eng.2013.55b005 Published Online May 2013 (http://www.scirp.org/journal/eng) Jogging and Walking Analysis Using Wearable Sensors * Ching ee ong, Rubita Sudirman,
Engineering, 2013, 5, 20-24 doi:10.4236/eng.2013.55b005 Published Online May 2013 (http://www.scirp.org/journal/eng) Jogging and Walking Analysis Using Wearable Sensors * Ching ee ong, Rubita Sudirman,
Figure 1 betois (bending torsion insole system) system with five measuring points and A/D- converter.
 Bending and Torsional Moments - A new measuring system for gait analysis Nora Dawin & Annette Kerkhoff & Klaus Peikenkamp, University of Applied Sciences Münster, Germany Abstract The Laboratory of Biomechanics
Bending and Torsional Moments - A new measuring system for gait analysis Nora Dawin & Annette Kerkhoff & Klaus Peikenkamp, University of Applied Sciences Münster, Germany Abstract The Laboratory of Biomechanics
Gait analysis through sound
 Invited article Niigata Journal of Health and Welfare Vol. 15, No. 1 Gait analysis through sound Kaoru Abe Graduate School of Health and Welfare, Niigata University of Health and Welfare, Niigata, Japan
Invited article Niigata Journal of Health and Welfare Vol. 15, No. 1 Gait analysis through sound Kaoru Abe Graduate School of Health and Welfare, Niigata University of Health and Welfare, Niigata, Japan
Gait Analysis at Your Fingertips:
 Gait Analysis at Your Fingertips: Enhancing Observational Gait Analysis Using Mobile Device Technology and the Edinburgh Visual Gait Scale Jon R. Davids, MD; Shriners Hospitals for Children Northern California;
Gait Analysis at Your Fingertips: Enhancing Observational Gait Analysis Using Mobile Device Technology and the Edinburgh Visual Gait Scale Jon R. Davids, MD; Shriners Hospitals for Children Northern California;
SCHEINWORKS Measuring and Analysis Systems by
 Pressure Measurement Systems for standing and walking analysis Germany since 1879 Pressure Measurement Systems for standing and walking analysis Documentation of Gait image Stance Symmetry of all parameters
Pressure Measurement Systems for standing and walking analysis Germany since 1879 Pressure Measurement Systems for standing and walking analysis Documentation of Gait image Stance Symmetry of all parameters
Emergent walking stop using 3-D ZMP modification criteria map for humanoid robot
 2007 IEEE International Conference on Robotics and Automation Roma, Italy, 10-14 April 2007 ThC9.3 Emergent walking stop using 3-D ZMP modification criteria map for humanoid robot Tomohito Takubo, Takeshi
2007 IEEE International Conference on Robotics and Automation Roma, Italy, 10-14 April 2007 ThC9.3 Emergent walking stop using 3-D ZMP modification criteria map for humanoid robot Tomohito Takubo, Takeshi
video Purpose Pathological Gait Objectives: Primary, Secondary and Compensatory Gait Deviations in CP AACPDM IC #3 1
 s in CP Disclosure Information AACPDM 71st Annual Meeting September 13-16, 2017 Speaker Names: Sylvia Ounpuu, MSc and Kristan Pierz, MD Differentiating Between, Secondary and Compensatory Mechanisms in
s in CP Disclosure Information AACPDM 71st Annual Meeting September 13-16, 2017 Speaker Names: Sylvia Ounpuu, MSc and Kristan Pierz, MD Differentiating Between, Secondary and Compensatory Mechanisms in
REPORT. A comparative study of the mechanical and biomechanical behaviour of natural turf and hybrid turf for the practise of sports
 REPORT A comparative study of the mechanical and biomechanical behaviour of natural turf and hybrid turf for the practise of sports Addressed to: PSF - PALAU TURF Date: May 2015 Table of Contents SHEET
REPORT A comparative study of the mechanical and biomechanical behaviour of natural turf and hybrid turf for the practise of sports Addressed to: PSF - PALAU TURF Date: May 2015 Table of Contents SHEET
Controlling Walking Behavior of Passive Dynamic Walker utilizing Passive Joint Compliance
 Controlling Walking Behavior of Passive Dynamic Walker utilizing Passive Joint Compliance Takashi TAKUMA, Koh HOSODA Department of Adaptive Machine Systems, Graduate School of Engineering Osaka University
Controlling Walking Behavior of Passive Dynamic Walker utilizing Passive Joint Compliance Takashi TAKUMA, Koh HOSODA Department of Adaptive Machine Systems, Graduate School of Engineering Osaka University
1B1 Meridium. Reclaim your way. Information for practitioners. Meridium Ottobock 1
 1B1 Meridium Reclaim your way. Information for practitioners Meridium Ottobock 1 Reclaim your way. With the development of the individualized Meridium prosthetic foot, Ottobock has incorporated the latest
1B1 Meridium Reclaim your way. Information for practitioners Meridium Ottobock 1 Reclaim your way. With the development of the individualized Meridium prosthetic foot, Ottobock has incorporated the latest
Decentralized Autonomous Control of a Myriapod Locomotion Robot
 Decentralized utonomous Control of a Myriapod Locomotion Robot hmet Onat Sabanci University, Turkey onat@sabanciuniv.edu Kazuo Tsuchiya Kyoto University, Japan tsuchiya@kuaero.kyoto-u.ac.jp Katsuyoshi
Decentralized utonomous Control of a Myriapod Locomotion Robot hmet Onat Sabanci University, Turkey onat@sabanciuniv.edu Kazuo Tsuchiya Kyoto University, Japan tsuchiya@kuaero.kyoto-u.ac.jp Katsuyoshi
Gait Analysis by High School Students
 Gait Analysis by High School Students André Heck 1 and Caroline van Dongen 2 1 AMSTEL Institute, University of Amsterdam, Amsterdam, The Netherlands, heck@science.uva.nl 2 St. Antoniuscollege, Gouda, The
Gait Analysis by High School Students André Heck 1 and Caroline van Dongen 2 1 AMSTEL Institute, University of Amsterdam, Amsterdam, The Netherlands, heck@science.uva.nl 2 St. Antoniuscollege, Gouda, The
Gait Analyser. Description of Walking Performance
 Gait Analyser Description of Walking Performance This brochure will help you to understand clearly the parameters described in the report of the Gait Analyser, provide you with tips to implement the walking
Gait Analyser Description of Walking Performance This brochure will help you to understand clearly the parameters described in the report of the Gait Analyser, provide you with tips to implement the walking
Gait Analysis System. User Manual and Outcome parameters Patent WO2012/ A1
 Gait Analysis System User Manual and Outcome parameters Patent WO212/7855 A1 Thank you for purchasing our Gait Analysis Package. Gait Up s goal is to provide you with a user-friendly setup to measure accurately
Gait Analysis System User Manual and Outcome parameters Patent WO212/7855 A1 Thank you for purchasing our Gait Analysis Package. Gait Up s goal is to provide you with a user-friendly setup to measure accurately
Normal and Abnormal Gait
 Normal and Abnormal Gait Adrielle Fry, MD EvergreenHealth, Division of Sport and Spine University of Washington Board Review Course March 6, 2017 What are we going to cover? Definitions and key concepts
Normal and Abnormal Gait Adrielle Fry, MD EvergreenHealth, Division of Sport and Spine University of Washington Board Review Course March 6, 2017 What are we going to cover? Definitions and key concepts
GROUND REACTION FORCE DOMINANT VERSUS NON-DOMINANT SINGLE LEG STEP OFF
 GROUND REACTION FORCE DOMINANT VERSUS NON-DOMINANT SINGLE LEG STEP OFF Sara Gharabaghli, Rebecca Krogstad, Sara Lynch, Sofia Saavedra, and Tamara Wright California State University, San Marcos, San Marcos,
GROUND REACTION FORCE DOMINANT VERSUS NON-DOMINANT SINGLE LEG STEP OFF Sara Gharabaghli, Rebecca Krogstad, Sara Lynch, Sofia Saavedra, and Tamara Wright California State University, San Marcos, San Marcos,
+ t1 t2 moment-time curves
 Part 6 - Angular Kinematics / Angular Impulse 1. While jumping over a hurdle, an athlete s hip angle was measured to be 2.41 radians. Within 0.15 seconds, the hurdler s hip angle changed to be 3.29 radians.
Part 6 - Angular Kinematics / Angular Impulse 1. While jumping over a hurdle, an athlete s hip angle was measured to be 2.41 radians. Within 0.15 seconds, the hurdler s hip angle changed to be 3.29 radians.
Disability assessment using visual gait analysis
 Disability assessment using visual gait analysis Sherif El-Sayed Hussein Computer and Systems Department, Mansoura University, Mansoura, Egypt Tel: +2 0122205369 Fax: +2 0502244690 E-mail: sherif_hussein@mans.edu.eg
Disability assessment using visual gait analysis Sherif El-Sayed Hussein Computer and Systems Department, Mansoura University, Mansoura, Egypt Tel: +2 0122205369 Fax: +2 0502244690 E-mail: sherif_hussein@mans.edu.eg
Brief Biomechanical Analysis on the Walking of Spinal Cord Injury Patients with a Lower Limb Exoskeleton Robot
 13 IEEE International Conference on Rehabilitation Robotics June 24-26, 13 Seattle, Washington USA Brief Biomechanical Analysis on the Walking of Spinal Cord Injury Patients with a Lower Limb Exoskeleton
13 IEEE International Conference on Rehabilitation Robotics June 24-26, 13 Seattle, Washington USA Brief Biomechanical Analysis on the Walking of Spinal Cord Injury Patients with a Lower Limb Exoskeleton
A Bio-inspired Behavior Based Bipedal Locomotion Control B4LC Method for Bipedal Upslope Walking
 1 A Bio-inspired Behavior Based Bipedal Locomotion Control B4LC Method for Bipedal Upslope Walking JIE ZHAO, QI LIU, STEFFEN SCHUETZ, and KARSTEN BERNS Robotics Research Lab, University of Kaiserslautern,
1 A Bio-inspired Behavior Based Bipedal Locomotion Control B4LC Method for Bipedal Upslope Walking JIE ZHAO, QI LIU, STEFFEN SCHUETZ, and KARSTEN BERNS Robotics Research Lab, University of Kaiserslautern,
Impact Points and Their Effect on Trajectory in Soccer
 Proceedings Impact Points and Their Effect on Trajectory in Soccer Kaoru Kimachi 1, *, Sungchan Hong 2, Shuji Shimonagata 3 and Takeshi Asai 2 1 Doctoral Program of Coaching Science, University of Tsukuba,
Proceedings Impact Points and Their Effect on Trajectory in Soccer Kaoru Kimachi 1, *, Sungchan Hong 2, Shuji Shimonagata 3 and Takeshi Asai 2 1 Doctoral Program of Coaching Science, University of Tsukuba,
Sample Solution for Problem 1.a
 Sample Solution for Problem 1.a 1 Inverted Pendulum Model (IPM) 1.1 Equations of Motion and Ground Reaction Forces Figure 1: Scheme of the Inverted Pendulum Model (IPM). The equations of motion of this
Sample Solution for Problem 1.a 1 Inverted Pendulum Model (IPM) 1.1 Equations of Motion and Ground Reaction Forces Figure 1: Scheme of the Inverted Pendulum Model (IPM). The equations of motion of this
ASSESMENT Introduction REPORTS Running Reports Walking Reports Written Report
 ASSESMENT REPORTS Introduction Left panel Avatar Playback Right Panel Patient Gait Parameters Report Tab Click on parameter to view avatar at that point in time 2 Introduction Software will compare gait
ASSESMENT REPORTS Introduction Left panel Avatar Playback Right Panel Patient Gait Parameters Report Tab Click on parameter to view avatar at that point in time 2 Introduction Software will compare gait
Walking with coffee: when and why coffee spills
 Walking with coffee: when and why coffee spills Hans C. Mayer and Rouslan Krechetnikov Department of Mechanical Engineering University of California at Santa Barbara February 20-24, 2012 Page 1/25 Motivation
Walking with coffee: when and why coffee spills Hans C. Mayer and Rouslan Krechetnikov Department of Mechanical Engineering University of California at Santa Barbara February 20-24, 2012 Page 1/25 Motivation
Increasing ankle push-off work with a powered prosthesis does not necessarily reduce metabolic rate for transtibial amputees
 Supplementary Materials Increasing ankle push-off work with a powered prosthesis does not necessarily reduce metabolic rate for transtibial amputees Roberto E. Quesada, Joshua M. Caputo,, and Steven H.
Supplementary Materials Increasing ankle push-off work with a powered prosthesis does not necessarily reduce metabolic rate for transtibial amputees Roberto E. Quesada, Joshua M. Caputo,, and Steven H.
A Biomechanical Approach to Javelin. Blake Vajgrt. Concordia University. December 5 th, 2012
 A Biomechanical Approach to Javelin Blake Vajgrt Concordia University December 5 th, 2012 The Biomechanical Approach to Javelin 2 The Biomechanical Approach to Javelin Javelin is one of the four throwing
A Biomechanical Approach to Javelin Blake Vajgrt Concordia University December 5 th, 2012 The Biomechanical Approach to Javelin 2 The Biomechanical Approach to Javelin Javelin is one of the four throwing
Humanoid Robots and biped locomotion. Contact: Egidio Falotico
 Humanoid Robots and biped locomotion Contact: Egidio Falotico e.falotico@sssup.it Outline What is a Humanoid? Why Develop Humanoids? Challenges in Humanoid robotics Active vs Passive Locomotion Active
Humanoid Robots and biped locomotion Contact: Egidio Falotico e.falotico@sssup.it Outline What is a Humanoid? Why Develop Humanoids? Challenges in Humanoid robotics Active vs Passive Locomotion Active
EXPERIMENTAL STUDY OF EXOSKELETON FOR ANKLE AND KNEE JOINT
 EXPERIMENTAL STUDY OF EXOSKELETON FOR ANKLE AND KNEE JOINT PROJECT REFERENCE NO. : 37S0925 COLLEGE : NEW HORIZON COLLEGE OF ENGINEERING, BANGALORE BRANCH : MECHANICAL ENGINEERING GUIDES : DR GANESHA PRASAD
EXPERIMENTAL STUDY OF EXOSKELETON FOR ANKLE AND KNEE JOINT PROJECT REFERENCE NO. : 37S0925 COLLEGE : NEW HORIZON COLLEGE OF ENGINEERING, BANGALORE BRANCH : MECHANICAL ENGINEERING GUIDES : DR GANESHA PRASAD
EXSC 408L Fall '03 Problem Set #2 Linear Motion. Linear Motion
 Problems: 1. Once you have recorded the calibration frame for a data collection, why is it important to make sure the camera does not shut off? hat happens if the camera automatically shuts off after being
Problems: 1. Once you have recorded the calibration frame for a data collection, why is it important to make sure the camera does not shut off? hat happens if the camera automatically shuts off after being
Current issues regarding induced acceleration analysis of walking using the integration method to decompose the GRF
 Current issues regarding induced acceleration analysis of walking using the integration method to decompose the GRF George Chen May 17, 2002 Stanford Neuromuscular Biomechanics Lab Group Muscle contribution
Current issues regarding induced acceleration analysis of walking using the integration method to decompose the GRF George Chen May 17, 2002 Stanford Neuromuscular Biomechanics Lab Group Muscle contribution
ZMP Trajectory Generation for Reduced Trunk Motions of Biped Robots
 ZMP Trajectory Generation for Reduced Trunk Motions of Biped Robots Jong H. Park School of Mechanical Engineering Hanyang University Seoul, 33-79, Korea email:jong.park@ieee.org Yong K. Rhee School of
ZMP Trajectory Generation for Reduced Trunk Motions of Biped Robots Jong H. Park School of Mechanical Engineering Hanyang University Seoul, 33-79, Korea email:jong.park@ieee.org Yong K. Rhee School of
Robot motion by simultaneously wheel and leg propulsion
 Robot motion by simultaneously wheel and leg propulsion Aarne Halme, Ilkka Leppänen, Miso Montonen, Sami Ylönen Automation Technology Laboratory Helsinki University of Technology PL 5400, 02015 HUT, Finland
Robot motion by simultaneously wheel and leg propulsion Aarne Halme, Ilkka Leppänen, Miso Montonen, Sami Ylönen Automation Technology Laboratory Helsinki University of Technology PL 5400, 02015 HUT, Finland
AN31E Application Note
 Balancing Theory Aim of balancing How an unbalance evolves An unbalance exists when the principle mass axis of a rotating body, the so-called axis of inertia, does not coincide with the rotational axis.
Balancing Theory Aim of balancing How an unbalance evolves An unbalance exists when the principle mass axis of a rotating body, the so-called axis of inertia, does not coincide with the rotational axis.
Walking and Running BACKGROUND REVIEW. Planar Pendulum. BIO-39 October 30, From Oct. 25, Equation of motion (for small θ) Solution is
 Walking and Running BIO-39 October 30, 2018 BACKGROUND REVIEW From Oct. 25, 2018 Planar Pendulum Equation of motion (for small θ) 2 d g 0 2 dt Solution is Where: g is acceleration due to gravity l is pendulum
Walking and Running BIO-39 October 30, 2018 BACKGROUND REVIEW From Oct. 25, 2018 Planar Pendulum Equation of motion (for small θ) 2 d g 0 2 dt Solution is Where: g is acceleration due to gravity l is pendulum
Development of a Simulation Model for Swimming with Diving Fins
 Proceedings Development of a Simulation Model for Swimming with Diving Fins Motomu Nakashima 1, *, Yosuke Tanno 2, Takashi Fujimoto 3 and Yutaka Masutani 3 1 Department of Systems and Control Engineering,
Proceedings Development of a Simulation Model for Swimming with Diving Fins Motomu Nakashima 1, *, Yosuke Tanno 2, Takashi Fujimoto 3 and Yutaka Masutani 3 1 Department of Systems and Control Engineering,
Purpose. Outline. Angle definition. Objectives:
 Disclosure Information AACPDM 69 th Annual Meeting October 21-24, 2015 Speaker Names: Sylvia Õunpuu, MSc and Kristan Pierz, MD Gait Analysis Data Interpretation: Understanding Kinematic Relationships Within
Disclosure Information AACPDM 69 th Annual Meeting October 21-24, 2015 Speaker Names: Sylvia Õunpuu, MSc and Kristan Pierz, MD Gait Analysis Data Interpretation: Understanding Kinematic Relationships Within
A NEURAL PROSTHESIS TO IMPROVE GAIT IN PEOPLE WITH MUSCLE WEAKNESS
 A NEURAL PROSTHESIS TO IMPROVE GAIT IN PEOPLE WITH MUSCLE WEAKNESS A thesis presented to the faculty of the Graduate School of Western Carolina University in partial fulfillment of the requirements for
A NEURAL PROSTHESIS TO IMPROVE GAIT IN PEOPLE WITH MUSCLE WEAKNESS A thesis presented to the faculty of the Graduate School of Western Carolina University in partial fulfillment of the requirements for
C-Brace Orthotronic Mobility System
 C-Brace Orthotronic Mobility System You ll always remember your first step Information for practitioners C-Brace Orthotics reinvented Until now, you and your patients with conditions like incomplete spinal
C-Brace Orthotronic Mobility System You ll always remember your first step Information for practitioners C-Brace Orthotics reinvented Until now, you and your patients with conditions like incomplete spinal
The Starting Point. Prosthetic Alignment in the Transtibial Amputee. Outline. COM Motion in the Coronal Plane
 Prosthetic Alignment in the Transtibial Amputee The Starting Point David C. Morgenroth, MD, Department of Rehabilitation Medicine University of Washington VAPSHCS Outline COM Motion in the Coronal Plane
Prosthetic Alignment in the Transtibial Amputee The Starting Point David C. Morgenroth, MD, Department of Rehabilitation Medicine University of Washington VAPSHCS Outline COM Motion in the Coronal Plane
Available online at ScienceDirect. Procedia Engineering 112 (2015 )
 Available online at www.sciencedirect.com ScienceDirect Procedia Engineering 112 (2015 ) 196 201 7th Asia-Pacific Congress on Sports Technology, APCST 2015 Dynamics of spin bowling: the normalized precession
Available online at www.sciencedirect.com ScienceDirect Procedia Engineering 112 (2015 ) 196 201 7th Asia-Pacific Congress on Sports Technology, APCST 2015 Dynamics of spin bowling: the normalized precession
Generation of Robot Motion Based on Measurement of Human Movement. Susumu Sakano 1, Satoru Shoji 1
 Generation of Robot Motion Based on Measurement of Human Movement Susumu Sakano 1, Satoru Shoji 1 1College of Engineering, Nihon University 1 Nakagawara Tokusada Tamura-machi Koriyama 963-8642 Japan Tel;
Generation of Robot Motion Based on Measurement of Human Movement Susumu Sakano 1, Satoru Shoji 1 1College of Engineering, Nihon University 1 Nakagawara Tokusada Tamura-machi Koriyama 963-8642 Japan Tel;
DIFFERENCE BETWEEN TAEKWONDO ROUNDHOUSE KICK EXECUTED BY THE FRONT AND BACK LEG - A BIOMECHANICAL STUDY
 268 Isas 2000! Hong Kong DIFFERENCE BETWEEN TAEKWONDO ROUNDHOUSE KICK EXECUTED BY THE FRONT AND BACK LEG - A BIOMECHANICAL STUDY Pui-Wah Kong, Tze-Chung Luk and Youlian Hong The Chinese University of Hong
268 Isas 2000! Hong Kong DIFFERENCE BETWEEN TAEKWONDO ROUNDHOUSE KICK EXECUTED BY THE FRONT AND BACK LEG - A BIOMECHANICAL STUDY Pui-Wah Kong, Tze-Chung Luk and Youlian Hong The Chinese University of Hong
A NEW GOLF-SWING ROBOT MODEL UTILIZING SHAFT ELASTICITY
 Journal of Sound and Vibration (1998) 17(1), 17 31 Article No. sv981733 A NEW GOLF-SWING ROBOT MODEL UTILIZING SHAFT ELASTICITY S. SUZUKI Department of Mechanical System Engineering, Kitami Institute of
Journal of Sound and Vibration (1998) 17(1), 17 31 Article No. sv981733 A NEW GOLF-SWING ROBOT MODEL UTILIZING SHAFT ELASTICITY S. SUZUKI Department of Mechanical System Engineering, Kitami Institute of
Geometric moments for gait description
 Geometric moments for gait description C. Toxqui-Quitl, V. Morales-Batalla, A. Padilla-Vivanco, and C. Camacho-Bello. Universidad Politécnica de Tulancingo, Ingenierías 100, 43629 Hidalgo, México. ctoxqui@upt.edu.mx
Geometric moments for gait description C. Toxqui-Quitl, V. Morales-Batalla, A. Padilla-Vivanco, and C. Camacho-Bello. Universidad Politécnica de Tulancingo, Ingenierías 100, 43629 Hidalgo, México. ctoxqui@upt.edu.mx
PURPOSE. METHODS Design
 7 Murrary, M.P.; Sepic, S.B.; Gardner, G.M.; and Mollinger, L.A., "Gait patterns of above-knee amputees using constant-friction knee components," Bull Prosthet Res, 17(2):35-45, 1980. 8 Godfrey, C.M.;
7 Murrary, M.P.; Sepic, S.B.; Gardner, G.M.; and Mollinger, L.A., "Gait patterns of above-knee amputees using constant-friction knee components," Bull Prosthet Res, 17(2):35-45, 1980. 8 Godfrey, C.M.;
Meridium. Reclaim your way. Information for clinicians
 Meridium Reclaim your way. Information for clinicians Reclaim your way. With the development of the individualised Meridium prosthetic foot, Ottobock has incorporated the latest technology to achieve a
Meridium Reclaim your way. Information for clinicians Reclaim your way. With the development of the individualised Meridium prosthetic foot, Ottobock has incorporated the latest technology to achieve a
Towards determining absolute velocity of freestyle swimming using 3-axis accelerometers
 Towards determining absolute velocity of freestyle swimming using 3-axis accelerometers Author Stamm, Andy, Thiel, David, Burkett, Brendan, James, Daniel Published 2011 Journal Title Procedia Engineering
Towards determining absolute velocity of freestyle swimming using 3-axis accelerometers Author Stamm, Andy, Thiel, David, Burkett, Brendan, James, Daniel Published 2011 Journal Title Procedia Engineering
Normal Gait and Dynamic Function purpose of the foot in ambulation. Normal Gait and Dynamic Function purpose of the foot in ambulation
 Normal Gait and Dynamic Function purpose of the foot in ambulation Edward P. Mulligan, PT, DPT, OCS, SCS, ATC Assistant Professor; Residency Chair UT Southwestern School of Health Professions Department
Normal Gait and Dynamic Function purpose of the foot in ambulation Edward P. Mulligan, PT, DPT, OCS, SCS, ATC Assistant Professor; Residency Chair UT Southwestern School of Health Professions Department
Characteristics of ball impact on curve shot in soccer
 Available online at www.sciencedirect.com Procedia Engineering 60 (2013 ) 249 254 6 th Asia-Pacific Congress on Sports Technology (APCST) Characteristics of ball impact on curve shot in soccer Sungchan
Available online at www.sciencedirect.com Procedia Engineering 60 (2013 ) 249 254 6 th Asia-Pacific Congress on Sports Technology (APCST) Characteristics of ball impact on curve shot in soccer Sungchan
PERCEPTIVE ROBOT MOVING IN 3D WORLD. D.E- Okhotsimsky, A.K. Platonov USSR
 PERCEPTIVE ROBOT MOVING IN 3D WORLD D.E- Okhotsimsky, A.K. Platonov USSR Abstract. This paper reflects the state of development of multilevel control algorithms for a six-legged mobile robot. The robot
PERCEPTIVE ROBOT MOVING IN 3D WORLD D.E- Okhotsimsky, A.K. Platonov USSR Abstract. This paper reflects the state of development of multilevel control algorithms for a six-legged mobile robot. The robot
WalkOn product range. Dynamic Ankle-Foot Orthoses. Information for specialist dealers
 WalkOn product range Dynamic Ankle-Foot Orthoses Information for specialist dealers WalkOn Flex WalkOn WalkOn Trimable WalkOn Reaction WalkOn Reaction plus One range Many different applications The WalkOn
WalkOn product range Dynamic Ankle-Foot Orthoses Information for specialist dealers WalkOn Flex WalkOn WalkOn Trimable WalkOn Reaction WalkOn Reaction plus One range Many different applications The WalkOn
Available online at ScienceDirect. Procedia Computer Science 76 (2015 )
 Available online at www.sciencedirect.com ScienceDirect Procedia Computer Science 76 (2015 ) 257 263 2015 IEEE International Symposium on Robotics and Intelligent Sensors (IRIS 2015) Walking-Assisted Gait
Available online at www.sciencedirect.com ScienceDirect Procedia Computer Science 76 (2015 ) 257 263 2015 IEEE International Symposium on Robotics and Intelligent Sensors (IRIS 2015) Walking-Assisted Gait
Sensing and Modeling of Terrain Features using Crawling Robots
 Czech Technical University in Prague Sensing and Modeling of Terrain Features using Crawling Robots Jakub Mrva 1 Faculty of Electrical Engineering Agent Technology Center Computational Robotics Laboratory
Czech Technical University in Prague Sensing and Modeling of Terrain Features using Crawling Robots Jakub Mrva 1 Faculty of Electrical Engineering Agent Technology Center Computational Robotics Laboratory
Step Detection Algorithm For Accurate Distance Estimation Using Dynamic Step Length
 Step Detection Algorithm For Accurate Distance Estimation Using Dynamic Step Length Ahmad Abadleh ahmad_a@mutah.edu.jo Eshraq Al-Hawari eshraqh@mutah.edu.jo Esra'a Alkafaween Esra_ok@mutah.edu.jo Hamad
Step Detection Algorithm For Accurate Distance Estimation Using Dynamic Step Length Ahmad Abadleh ahmad_a@mutah.edu.jo Eshraq Al-Hawari eshraqh@mutah.edu.jo Esra'a Alkafaween Esra_ok@mutah.edu.jo Hamad
Gait Analysis Using Wearable Sensors
 Sensors 2012, 12, 2255-2283; doi:10.3390/s120202255 Review OPEN ACCESS sensors ISSN 1424-8220 www.mdpi.com/journal/sensors Gait Analysis Using Wearable Sensors Weijun Tao 1, Tao Liu 2, *, Rencheng Zheng
Sensors 2012, 12, 2255-2283; doi:10.3390/s120202255 Review OPEN ACCESS sensors ISSN 1424-8220 www.mdpi.com/journal/sensors Gait Analysis Using Wearable Sensors Weijun Tao 1, Tao Liu 2, *, Rencheng Zheng
The technique of reciprocal walking using the hip guidance orthosis (hgo) with crutches
 The technique of reciprocal walking using the hip guidance orthosis (hgo) with crutches P. B. BUTLER, R. E. MAJOR and J. H. PATRICK Orthotic Research and Locomotor Assessment Unit, The Robert Jones and
The technique of reciprocal walking using the hip guidance orthosis (hgo) with crutches P. B. BUTLER, R. E. MAJOR and J. H. PATRICK Orthotic Research and Locomotor Assessment Unit, The Robert Jones and
Fall Prevention Midterm Report. Akram Alsamarae Lindsay Petku 03/09/2014 Dr. Mansoor Nasir
 Fall Prevention Midterm Report Akram Alsamarae Lindsay Petku 03/09/2014 Dr. Mansoor Nasir Updates to timeline Last semester we created a timeline that included important milestones. We have narrowed down
Fall Prevention Midterm Report Akram Alsamarae Lindsay Petku 03/09/2014 Dr. Mansoor Nasir Updates to timeline Last semester we created a timeline that included important milestones. We have narrowed down
Novel Technique for Gait Analysis Using Two Waist Mounted Gyroscopes
 Old Dominion University ODU Digital Commons Computer Science Theses & Dissertations Computer Science Summer 2018 Novel Technique for Gait Analysis Using Two Waist Mounted Gyroscopes Ahmed Nasr Old Dominion
Old Dominion University ODU Digital Commons Computer Science Theses & Dissertations Computer Science Summer 2018 Novel Technique for Gait Analysis Using Two Waist Mounted Gyroscopes Ahmed Nasr Old Dominion
WATER HYDRAULIC HIGH SPEED SOLENOID VALVE AND ITS APPLICATION
 WATER HYDRAULIC HIGH SPEED SOLENOID VALVE AND ITS APPLICATION Akihito MITSUHATA *, Canghai LIU *, Ato KITAGAWA * and Masato KAWASHIMA ** * Department of Mechanical and Control Engineering, Graduate school
WATER HYDRAULIC HIGH SPEED SOLENOID VALVE AND ITS APPLICATION Akihito MITSUHATA *, Canghai LIU *, Ato KITAGAWA * and Masato KAWASHIMA ** * Department of Mechanical and Control Engineering, Graduate school
Ecole doctorale SMAER Sciences Mécaniques, Acoustique, Electronique, Robotique
 Thesis subject 2017 Laboratory : Institut des Systèmes Intelligents et de Robotiques (ISIR) CNRS UMR 7222 University: Université Pierre et Marie Curie Title of the thesis: Development of a Body-Machine-Interface
Thesis subject 2017 Laboratory : Institut des Systèmes Intelligents et de Robotiques (ISIR) CNRS UMR 7222 University: Université Pierre et Marie Curie Title of the thesis: Development of a Body-Machine-Interface
Toward a Human-like Biped Robot with Compliant Legs
 Book Title Book Editors IOS Press, 23 1 Toward a Human-like Biped Robot with Compliant Legs Fumiya Iida a,b,1, Yohei Minekawa a Juergen Rummel a and Andre Seyfarth a a Locomotion Laboratory, University
Book Title Book Editors IOS Press, 23 1 Toward a Human-like Biped Robot with Compliant Legs Fumiya Iida a,b,1, Yohei Minekawa a Juergen Rummel a and Andre Seyfarth a a Locomotion Laboratory, University
Aalborg Universitet. Published in: Sensors. DOI (link to publication from Publisher): /s Creative Commons License CC BY 4.
 Aalborg Universitet Estimation of ground reaction forces and moments during gait using only inertial motion capture Karatsidis, Angelos; Bellusci, Giovanni; Schepers, H. Martin; de Zee, Mark; Andersen,
Aalborg Universitet Estimation of ground reaction forces and moments during gait using only inertial motion capture Karatsidis, Angelos; Bellusci, Giovanni; Schepers, H. Martin; de Zee, Mark; Andersen,
Does Ski Width Influence Muscle Action in an Elite Skier? A Case Study. Montana State University Movement Science Laboratory Bozeman, MT 59717
 Does Ski Width Influence Muscle Action in an Elite Skier? A Case Study John G. Seifert 1, Heidi Nunnikhoven 1, Cory Snyder 1, Ronald Kipp 2 1 Montana State University Movement Science Laboratory Bozeman,
Does Ski Width Influence Muscle Action in an Elite Skier? A Case Study John G. Seifert 1, Heidi Nunnikhoven 1, Cory Snyder 1, Ronald Kipp 2 1 Montana State University Movement Science Laboratory Bozeman,
AN ACTIVITY MONITORING SYSTEM FOR ELDERLY
 AN ACTIVITY MONITORING SYSTEM FOR ELDERLY Kian Sek Tee, Afiqa Hairennas Binti Zulkifli and Chin Fhong Soon Faculty of Electrical and Electronic Engineering, University Tun Hussein Onn Malaysia, Parit Raja,
AN ACTIVITY MONITORING SYSTEM FOR ELDERLY Kian Sek Tee, Afiqa Hairennas Binti Zulkifli and Chin Fhong Soon Faculty of Electrical and Electronic Engineering, University Tun Hussein Onn Malaysia, Parit Raja,
Compliance for a cross four-bar knee joint
 Compliance for a cross four-bar knee joint Arnaud Hamon, Yannick Aoustin To cite this version: Arnaud Hamon, Yannick Aoustin. Compliance for a cross four-bar knee joint. The 14th International Conference
Compliance for a cross four-bar knee joint Arnaud Hamon, Yannick Aoustin To cite this version: Arnaud Hamon, Yannick Aoustin. Compliance for a cross four-bar knee joint. The 14th International Conference
Balance and knee extensibility evaluation of hemiplegic gait using an inertial body sensor network
 Guo et al. BioMedical Engineering OnLine 213, 12:83 RESEARCH Open Access Balance and knee extensibility evaluation of hemiplegic gait using an inertial body sensor network Yanwei Guo 1,2, Guoru Zhao 1,
Guo et al. BioMedical Engineering OnLine 213, 12:83 RESEARCH Open Access Balance and knee extensibility evaluation of hemiplegic gait using an inertial body sensor network Yanwei Guo 1,2, Guoru Zhao 1,
Smart shoe-based evaluation of gait phase detection accuracy using body-worn accelerometers
 Paper draft - please export an up-to-date reference from http://www.iet.unipi.it/m.cimino/pub Smart shoe-based evaluation of gait phase detection accuracy using body-worn accelerometers Marco Avvenuti
Paper draft - please export an up-to-date reference from http://www.iet.unipi.it/m.cimino/pub Smart shoe-based evaluation of gait phase detection accuracy using body-worn accelerometers Marco Avvenuti
Journal of Chemical and Pharmaceutical Research, 2016, 8(6): Research Article. Walking Robot Stability Based on Inverted Pendulum Model
 Available online www.jocpr.com Journal of Chemical and Pharmaceutical Research, 2016, 8(6):463-467 Research Article ISSN : 0975-7384 CODEN(USA) : JCPRC5 Walking Robot Stability Based on Inverted Pendulum
Available online www.jocpr.com Journal of Chemical and Pharmaceutical Research, 2016, 8(6):463-467 Research Article ISSN : 0975-7384 CODEN(USA) : JCPRC5 Walking Robot Stability Based on Inverted Pendulum
