Mechanics of dog walking compared with a passive, stiff-limbed, 4-bar linkage model, and their collisional implications
|
|
|
- Oswin Parrish
- 6 years ago
- Views:
Transcription
1 533 The Journal of Experimental Biology 1, Published by The Company of Biologists 7 doi:1.14/jeb.647 Mechanics of dog walking compared with a passive, stiff-limbed, 4-bar linkage model, and their collisional implications James R. Usherwood*, Sarah B. Williams and Alan M. Wilson The Royal Veterinary College, North Mymms, Hatfield, Herts, AL9 7TA, UK *Author for correspondence ( jusherwood@rvc.ac.uk) Accepted 13 November 6 Here, we present a simple stiff-limbed passive model of quadrupedal walking, compare mechanics predicted from the model with those observed from forceplate measurements of walking dogs and consider the implications of deviation from model predictions, especially with reference to collision mechanics. The model is based on the geometry of a 4-bar linkage consisting of a stiff hindleg, back, foreleg and the ground between the hind and front feet. It uses empirical morphological and kinematic inputs to determine the fluctuations in potential and kinetic energy, vertical and horizontal forces and energy losses associated with inelastic collisions at each foot placement. Using forceplate measurements to calculate centre of mass motions of walking dogs, we find Summary that (1) dogs may, but are not required to, spend periods of double support (one hind- and one forefoot) agreeing with the passive model; () legs are somewhat compliant, and mechanical energy fluctuates during triple support, with mechanical energy being lost directly after hindfoot placement and replaced following forefoot placement. Footfall timings and timing of mechanical energy fluctuations are consistent with strategies to reduce collisional forces, analogous to the suggested role of ankle extension as an efficient powering mechanism in human walking. Key words: collision, inverted pendulum, walk, quadruped. Introduction Walking with relatively stiff limbs, vaulting the hips (or hips and shoulders in the case of quadrupeds) over incompliant legs, presents a strategy for limiting the cost of locomotion. With this gait, mechanical energy forms interchange for free potential energy converts to kinetic as the centre of mass (COM) falls, and returns to potential as it rises again so walking in bipeds is often described in terms of an inverted pendulum (e.g. Cavagna et al., 1977). While fluctuations in kinetic and potential energy of the COM are also largely out of phase in walking quadrupeds (Cavagna et al., 1977) including dogs (Griffin et al., 4), the mechanics of quadrupedal walking is generally less clear: although kinetic and potential energy oscillations can be broadly out of phase, the degree to which limbs can be treated as stiff, inverted pendulums is uncertain. Consideration of passive dynamic walking for bipeds (McGeer, 199; Garcia et al., 1998) and quadrupeds (Smith and Berkemeir, 1997) subjectively shows remarkably life-like motions with simple stiff-limbed machines powered only by changes in potential energy due to walking down a gentle slope in order to overcome collisional losses. The relevance of the energetic cost of collisions at each limb placement is being increasingly understood in a variety of locomotory systems, including bipedal walking (Kuo, ; Donelan et al., ; Collins et al., 5), gibbon brachiation (Usherwood and Bertram, 3) and horse galloping (Ruina et al., 5). Here, we discuss some of the implications of minimising or managing collisions in quadrupedal walking and their potential use in accounting for observed footfall patterns and powering strategies. As highlighted by Aristotle, Again, why do quadrupeds move their legs criss-cross? We have to examine the reasons for all these facts, and others cognate to them; that the facts are such is clear from our Natural History, we have now to ask reasons for the facts. In an effort to approach this issue in the case of quadrupedal walking, we present a passive model based on the geometry of a 4-bar linkage to show (1) the fluctuations in potential and kinetic energy, () the vertical and horizontal forces, and (3) the mechanical energy losses that would be associated with each foot placement for a stiff-limbed, walking quadruped represented as a pair of inverted pendulums linked by a stiff, incompressible back. This model is not intended to accurately predict the kinetics, forces or energetics of actual quadrupedal walking; rather, it provides a reductionist position, from which the observed deviations from the passive, stifflimbed case can be highlighted and their implications discussed.
2 534 J. R. Usherwood, S. B. Williams and A. M. Wilson Materials and methods Here we present methods for: (1) a simple model of quadrupedal walking based on the geometry of a 4-bar linkage, predicting fluctuations in potential and kinetic energies, and horizontal and vertical accelerations, for passive, stiff-limbed quadrupeds; () extension of the model to derive energy losses due to collision as functions of limb phase and powering strategy; (3) empirical determination of fluctuations in potential and kinetic energies, horizontal and vertical accelerations, and power from forceplate and kinematic measurements; and (4) quantitative comparison of the model and observed fluctuations in potential and kinetic energies to determine the degree to which quadrupedal walking is passive (with a high energy recovery ) and stiff-limbed (with a high value of the novel parameter compression ratio ). Further comparisons between model and empirical observations in this manuscript are qualitative. Model construction Phase As walking can be considered a symmetrical gait, the footfall pattern can be described usefully in terms of phase ( ), expressed as a percentage throughout, where = T H1 F1 / T. (1) T H1 F1 is the time period between the first hindfoot and the first forefoot making contact with the ground as a proportion of the complete stride time (T) (the period between successive contacts with the same foot double the period of a step). We assume symmetry between left and right throughout: the first hind foot hits the ground at % of stride period, the first front foot at % and the second hind foot at 5%. As an example, an evenly spaced Hind-Fore-Hind-Fore-Hind (H-F-H-F) footfall pattern would have a phase of 5%. Phases less than 5% are biased towards H-F H-F H. Note that, with this definition, left and right make no difference; a stride can begin with either left hind- or right hindfoot. Note that the model uses a subtly different form of phase [the geometric phase ( geom ), see below], but this has an imperceptible bearing on the results. Numerical 4-bar model The model reduces quadrupedal walking to a 4-bar linkage (Fig. 1) that continuously conserves mechanical energy (although see the collisions calculations section on powering strategies). The geometry of the path of the hips and shoulders is determined by a compass gait for hind- and forelimbs, and a linkage between hips and shoulders provided by an incompressible, rigid back. This can be viewed as a 4-bar linkage consisting of a mass-less hindleg, a back with a distributed mass, a mass-less front leg and the static ground between the front and hind feet. This geometry determines the height, and thus potential energy, of the COM at every hindleg angle ( ) (taken from the vertical). Swing legs are disregarded. We calculate the appropriate geometry for the 4- bar linkage for the full range of hindlimb angles from hind to + hind (repeated to make two steps, or one stride, Fig. 1B). For each small change in hindlimb angle (a 15th of hind, so approximately.18 in our simulations), the time interval is calculated that results in the appropriate linear and angular velocities required for the kinetic energies to combine with potential energy to result in a constant total mechanical energy (see Usherwood and Bertram, 3). With the additional assumption that the limbs sweep through equal angles before and after the vertical, the only required inputs are as follows. Morphological: hind- and foreleg lengths (L hind, L fore ); body mass (m b ); bias of body mass towards the shoulders [p, which we take as 6% following Jayes and Alexander (Jayes and Alexander, 1978), Lee et al. (Lee et al., 1999) and Griffin et al. (Griffin et al., 4)]; and body moment of inertia about the COM (I). Kinematic: the mean horizontal velocity V, which with stride period T is used to determine hind (below) and the limb phase ( ). By iteration, the total mechanical energy of the system is found that results in the observed net forward velocity (V). The maximum angle swept from the vertical of the hindlimb ( hind ) is given by: z position (m) A Hip B hind = sin 1 (VT / 4L hind ). () COM θ hind L hind L fore Shoulder θ fore* Direction of motion x position (m) Fig. 1. Model geometry. (A) A 4-bar linkage consisting of a stiff hindleg (red, length L hind ), back, foreleg (blue, length L fore ) and the ground between the hind and front feet. The path of the body centre of mass (COM) and its rotations are calculated from purely geometric considerations as the hindleg vaults over the vertical (B). The stride begins at the instant of hindfoot placement. Both hind- and foreleg angles are assumed to sweep an equal angle before and after vertical. The initial foreleg angle fore * is determined from the phase. The hindlimb angle is incremented, changing COM position (green dots) and body angle, and the appropriate time step for each increment throughout the stride is calculated such that the total mechanical energy is constant (although see the powering strategies section). Interchanges between mechanical energy components (potential, kinetic and rotational kinetic energies), velocities and accelerations were thus calculated from the 4-bar linkage geometry as a function of time. Total mechanical energy was adjusted so that the model and observed mean horizontal velocities corresponded.
3 Mechanics of quadrupedal walking 535 This definition of hind is appropriate for use in the 4-bar model as the model assumes symmetry about the vertical and a duty factor (DF) of.5 (as the legs are infinitely stiff). True maximum sweep values are larger because the DF is >.5 during walking, and are somewhat biased so that the hindfoot travels further back than it does forwards with respect to the hip. However, the aim of the model is to make the simplest default position, with which to contrast empirical observation. We calculate an approximation of the moment of inertia (second moment of mass) of the body about the COM with the following assumptions: the mass distribution behind the COM is even and the distribution after the COM towards the shoulders is also even, but the mass is biased towards the shoulders such that p=.6. It turns out that modelled changes in rotational kinetic energy account for only a very small proportion of energy interchange (the amplitude in our simulations is typically 18 times less than for potential energy); therefore, we consider this very basic approximation for the moment of inertia to be adequate for the purposes of this study, and do not consider rotational kinetic energy further. The model uses a geometric form for phase ( geom ) as an input for the geometry: geom = ( fore + fore *) / 4 fore, (3) where fore is the maximum angle from vertical swept by the forelegs, and fore * is the angle of the forelegs from vertical at the instant of hindfoot placement (Fig. 1). As the magnitude of the velocity varies little throughout a stride, despite fluctuations in kinetic energy, the two forms for phase (Equations 1 and 3) give indistinguishable (<1% difference) values. Collision calculations The instantaneous change in velocity at each foot-on of the stiff-legged walking model is associated with a collision [see (Ruina et al., 5) for extensive discussion of collision mechanics]. Treating this collision as inelastic, a mechanical energetic cost of these collisions can be calculated from the velocity of the COM immediately before foot-on (v) and the step change in direction of the COM ( ) (Fig. ): v / v = cos( ), (4) where v is the velocity directly after the collision, before any energy return has taken place. From this, the ratio of post- and pre-collision kinetic energies (E k and E k, respectively) can be calculated: E k / E k = cos ( ). (5) Therefore, the energy lost with each sudden redirection of the COM trajectory at both hind and front foot placement can be calculated from the stiff-limbed 4-bar linkage model described above: E coll = E k E k = G m b v [1 cos ( )]. (6) It is worth noting that, although the magnitude of the accelerations (and so forces) at each collision is high v COM v γ Fig.. Collision geometry at foreleg contact. A component of the centre of mass (COM) velocity just prior to collision v can be maintained after the collision (v ) despite an inelastic redirection through an angle determined from the 4-bar linkage geometry. The collisional energy loss calculated at each leg contact is dependent on both velocity and the angle with which the COM path is suddenly deflected. (approaching infinite with a stiff-limbed model) and dependent on the simulation step size, energy losses associated with collision are finite and relatively insensitive to simulation step size. Model powering strategies For steady speed walking to be maintained, the energetic losses due to COM collision at each foot placement must be recovered over the stride cycle. The timing of energy return has a bearing on the collision energy losses and/or the speed that can be achieved for a given cost. For the completely stifflimbed walker, energy should ideally be put into the system only directly following a collision event, as this allows the greatest period at highest speed for a given collisional energy loss; any other energy input strategy would require higher velocities at the instant of collision (and so higher collisional energy losses) if the same average horizontal velocity was to be achieved. We therefore study the collision energy losses associated with three extreme energy input strategies: first, an immediate recovery of each energy loss directly after each collision (this is the strategy assumed in all previous sections); second, a recovery of energy only directly after forelimb contact (resulting in a reduced total mechanical energy between hindfoot contact and forefoot contact); third, a recovery of energy only directly after hindlimb contact. Note that, for fair comparison, the initial energy conditions are adjusted so that the mean speed is the same in each case. Empirical measurements Dogs and forceplate and integrations Five sound pet dogs covering a moderate range of sizes and proportions (Table 1) were walked over a forceplate, following procedures approved by the Royal Veterinary College. Speeds were selected at which each dog appeared to walk steadily without breaking into a trot or pausing. Non-dimensionalised speeds (Froude numbers Fr=V /gl hind, where g is the acceleration due to gravity) were calculated following Alexander and Jayes (Alexander and Jayes, 1983), using the hindlimb length (floor to hip during standing) as the
4 536 J. R. Usherwood, S. B. Williams and A. M. Wilson Table 1. Morphology and key kinematic variables for the five dogs Dog 1 Dog Dog 3* Dog 4 Dog 5 Breed Labrador Australian shepherd Australian shepherd Springer spaniel Bull terrier Sex Male Male Female Male Male Mass (kg) Hindlimb (m) Back (m) Forelimb (m) Number of trials Mean ± 1 s.d. hind ( ) 5.3±. 6.7±1. 3.4± ± ±.9 Mean phase ± 1 s.d. (%) 16.5±.9 1.9± ± ± ±1.5 *The dog for which example trials of very slow, slow and moderate walking (Fig. 3) were taken. Excluded from Fig. 4 as energy recovery was <5% throughout the Froude number range; this dog exhibited a bouncing gait even when kinematically walking. representative length. Basic two-dimensional kinematic parameters (from 4 Hz 5-camera Qualisys system; Qualisys, Gothenberg, Sweden) and ground reaction forces (from a Kistler 987BA; Kistler Instruments Ltd, Alton, UK) recording at 1 Hz and low-pass filtered at 5 Hz with a zero-lag digital fourth-order Butterworth filter were repeatedly recorded for single steps. Mean horizontal velocity, required as a model input and for forceplate integration (see below), was derived from motion of a marker sited on the trunk at approximately halfway down the seventh rib. Foot-on timings (required for limb phase, an input of the model) and foot-off timings (to show periods of triple support) were assessed from kinematic markers on the feet. Motions of the COM were calculated from the measured ground reaction forces, as were the associated changes in potential and kinetic energy, following the principles described by Cavagna (Cavagna, 1975). In order to minimise drift due to integrating or double-integrating over long periods, we used measurements for single steps (we use from hind-on to the contralateral hind-on) and duplicated the derived values, assuming walking to be a symmetrical gait, to provide results for a complete stride (two steps). In addition, it was assumed that there is no net change in COM height over a step (mean vertical velocity is zero), the mean horizontal velocity is that observed from kinematics and there is no net horizontal acceleration or deceleration. Unlike Cavagna (Cavagna, 1975), we include vertical kinetic energy in our calculation of kinetic energy. COM power (external mechanical power) is calculated from the changes in the sum of potential and kinetic energies for a small time-step ( t): P COM = (E p + E k ) / t. (7) Energy recovery and compression ratio To provide a quantitative assessment of the degree to which walking quadrupeds follow stiff-limbed, passive walking, we use both the widely discussed term energy recovery (e.g. Cavagna et al., 1977; Griffin et al., 4) and a new term, which we describe as a compression ratio (CR). Energy recovery describes the proportion of combined potential and kinetic energy fluctuation that could be achieved passively: ER = 1 E m / ( E k + E p ) = ( E k + E p E m )/ ( E k + E p ), (8) where E m is the total instantaneous mechanical (E p +E k ) energy. A value of 1 would suggest perfect E k -E p -E k interchange and a constant zero P COM. The CR is based on the variations in potential energy that would occur if the quadruped was stiff-limbed, using the observed morphology and foot kinematics. It is based on the amplitude of changes in energy, and takes no account of timing. It can be used as a measure of the degree to which limbs can be viewed as being stiff: CR = a Ep,obs / a Ep,mod, (9) where a Ep,obs is the amplitude of the forceplate-derived variation in potential energy, and a Ep,mod is that derived from the stiff-limbed model. A value of zero would show that the COM travelled in a completely level path; a value of 1 suggests that the COM changes height exactly as calculated from the rigid 4-bar linkage model. Note that this metric is only useful for walking: values near 1 can be achieved with trotting, but it should not then be inferred that stiff limbs are being used. Also note that for a walking biped, this would be simply CR biped = a Ep,obs / m b gl [1 cos( )], (1) where L is the leg length and the maximum leg angle from vertical. Results and discussion Model- and forceplate-derived results for three trials of one dog (Dog 3, an Australian Shepherd; Table 1) are shown in Fig. 3. The appropriate observed kinematic inputs (V,, T) from each trial were used as inputs to the model. These three trials were selected as they cover very slow, slow and moderate walking speeds, and deviations from the zero acceleration assumption used in the forceplate integrations were small
5 Mechanics of quadrupedal walking 537 (impulses over the integration period would have accounted maximally for a change in.6 m s 1 or.7 m s 1 in horizontal and vertical velocity, respectively). Each trace shows values for a complete stride, adjusted to start at hindfoot contact (derived from kinematics). Results for three of the four additional dogs broadly matched those for the moderate example trial (Fig. 3iii). The remaining dog, also the smallest, locomoted at an appropriate range of Froude numbers (.3.46) for walking dogs; however, this dog appeared to use a bouncing gait at these Froude numbers, with the energy recovery values often below 5%. Fluctuations in E p and E k : energy recovery and the compression ratio At low speeds, fluctuations in potential energy approach those predicted by the stifflimbed geometry (Fig. 3iA, and the CR of Fig. 4). However, this is associated with energy input as the COM rises, and loss as it falls again (Fig. 3iE), as indicated by the power profile, the low amplitude of the E k fluctuations (Fig. 3iB) and the diminished energy recovery [Fig. 4, matching the observations of Griffin et al. (Griffin et al., 4)]. At intermediate speeds, observed fluctuations in E p are of a lower amplitude and match the stiff-limbed model less well, presumably indicating that the limbs compress to a greater extent. However, E k -E p -E k energy interchange is more effective during periods of double support (one hindand one forefoot), suggesting passive stifflimbed or inverted pendulum mechanisms are effective: COM powers are low during this period (Fig. 3iiE), and energy recovery is at a maximum (Fig. 4) at these speeds. At higher walking speeds, the observed E p fluctuations flatten further, and COM powers are consistent with spring-like behaviour of the forelimbs, with mechanical energy lost during the first half of stance and recovered during the second half. This theme continues with increasing speed, with a reduction in both energy recovery (suggesting more spring-like behaviour and less stiff-limbed or inverted-pendulum energy interchange) and the CR (indicating that limbs compress to a greater extent). These results show the value of the term energy recovery and the proposed term compression ratio in the study of walking. Although energy recovery has proved effective in indicating the potential for passive E p -E k -E p interchange, it is unable to provide an indication of how important this interchange is. Consider a large animal walking with a near- Groucho gait (with a level, constant speed COM) that fluctuates E p and E k by only a very small amount. If this small ΔE p (J) ΔE k (J) a z (m s ) a x (m s ) COM power (W) A B C D E F H F V=.81 m s 1 Fr=.145 H1 F1 i ii iii H F V=.85 m s 1 Fr= Time (s) F H1 F1 H F V=1.14 m s 1 Fr=.88 H1 F1 fluctuation happened to be exactly out of phase, consideration of energy recovery alone might suggest that it was walking efficiently, while each limb performed massive internal negative and positive works [and, presumably, at high metabolic cost (Ortega and Farley, 5)]. Without resorting to leg-by-leg forceplate measurements and analysis, the CR provides an indication of the energy fluctuations that would be associated with stiff-limbed walking, and therefore how much weight to put on the consideration of the energy recovery term. So, there are two key questions to be asked when studying a walking animal: what proportion of the E k -E p -E k interchanges may be considered passive and to what extent might this be achieved using stiff limbs. Although a full inverse dynamics F H F Fig. 3. Observed and model energy fluctuations (A,B), accelerations (C,D) and powers (E) for three example walking strides ranging from very slow (i) through slow (ii) to moderate (iii). Model outcomes, derived using empirical kinematic inputs and the stifflimbed, constant energy (the immediate energy recovery strategy) model are shown in blue; values derived from forceplate measurements and kinematics are shown in red. Model accelerations go off-scale at the instants of each foot initial contact. Foot contact timings (F) can be used to identify periods of double and triple support.
6 538 J. R. Usherwood, S. B. Williams and A. M. Wilson CR Froude number Dog 1 Dog Dog 3 (example) Dog 4 Fig. 4. Combined summary results for four walking dogs over a range of speeds. Solid outlines relate to the left axis [compression ratio (CR)] and represent the observed fluctuations in potential energy as a proportion of those calculated from stiff-limbed 4-bar linkage geometry. Symbols with grey outlines relate to the right-hand axis [energy recovery (ER)] and represent the effectiveness of energy interchange between kinetic and potential energies (1 being perfect). Lines show quadratic fits. assessment of the walking animal is required to answer these questions fully, we consider energy recovery and CR to provide broad metrics for these two questions. Each of these terms indicates necessary but not adequate conditions for passive, ER stiff-limbed walking. High values of each can potentially be achieved with near-groucho (ER) or bouncing (CR) walking. High values for both, however, provide strong evidence for passive, stiff-limbed walking mechanics without the requirement of a full inverse dynamics analysis. Observed and model accelerations (forces) Deviations between observed and model vertical and horizontal accelerations can be broadly understood by consideration of a certain degree of limb compliance, increasing with speed. The model predicts very high accelerations (or forces) at the instant of each foot placement; forceplate records show that there is a delay between foot placement and peak force, and the force peaks are smoothed. Once this is taken into account, the model is effective in accounting for both horizontal and vertical accelerations, particularly during periods of double (one hind-, one forefoot) stance (Fig. 3C,D). With increasing speeds, the model predicts larger components of the vertical impulse to be contained in the collision spikes. Mean vertical acceleration remains zero (mean vertical force = body weight) but, while the COM arcs along its trajectory, centripetal acceleration requirements become apparent vertical accelerations during the majority of the stride fall below zero. The model indicates that this trend would continue with increasing speed until the dog requires vertical accelerations below 9.81 m s ; at this point there is insufficient gravity to keep the model dog in contact with the ground, and walking cannot be maintained. For the morphological and kinematic inputs of the medium trial ( hind =4.8, =13.%), this condition would occur at a Froude number of.84; with the same parameters but a phase of % Collision energy loss per step (J) 4 A B H-F H-F H F-H F- H-F-H-F- C D Phase (%) Phase (%) Fig. 5. Model collisional energy losses for a step with full ranges of forelimb hindlimb phases. A ±5% limb phase suggests exactly even timing between hind- and forefoot contacts (H-F-H-F-, represented by vertical grey broken lines). Dotted lines represent energy lost at hind-foot contact; broken lines the energy lost at forefoot contact; solid lines the total energy lost for a step (one hind- and one forefoot contact). Three hypothetical powering strategies are shown: immediate recovery of energy loss (black); energy recovery only directly after forefoot contact (red) (most realistic); energy recovery only after hindfoot contact (blue). (A) Results for a fore-aft symmetrical walking dog with even fore- and hindleg lengths and a centre of mass (COM) mid-way along the body. (B) As for A, but with a realistic bias in leg lengths (foreleg =.47 m, hindleg =.46 m). (C) As for A, but with a realistic bias in mass position, with the COM towards the shoulders (p=.6). (D) Results using realistic values of both limb length and mass bias. The underlying grey box represents the observed range of mean phases for walking dogs.
7 Mechanics of quadrupedal walking 539 or 5% (pacing or trotting footfall pattern), at Fr>.76; with a phase of 5%, at Fr>.84. This phenomenon, therefore, occurs at speeds considerably greater than those tested in this study. This speed limitation to walking is largely equivalent to that described by Alexander (1989) and Usherwood (5), traditionally understood using inverted pendulum mechanics to describe the centripetal acceleration requirements of stifflimbed walking. However, even at moderate Froude numbers, limb compliance smoothes the COM trajectories, thus reducing both the impulses attributable to the collision spikes, and the centripetal acceleration requirements, effectively spreading the weight support across the stance. Collision results Results from the collision model (Fig. 5) indicate the implications of bias in front/back leg length, fore/aft mass distribution, powering strategy and phase. A realistic bias in front/back leg length (Fig. 5B) has little bearing on collisional energy losses compared with equal leg lengths. The mass bias (Fig. 5C), however, has a notable effect: the collisional energy loss due to hindfoot contact (dotted lines) is reduced, while that due to forefoot contact (broken lines) is increased, resulting in ii A B i Hypothetical powering impulse Hip Smoothed COM path Fig. 6. Hypothetical propulsive impulses consistent with collision amelioration. If the mechanism for providing a powering impulse to the centre of mass (COM) also smoothes its path (A), powering is more efficient as collision losses are reduced. This may be achieved by two mechanisms (B): (i) hip torque while the hindleg is in early stance, or (ii) hindleg extension while the hindleg is late in stance. Either, or both, would have the effect of smoothing the path of the COM during forefoot placement, thus reducing the relatively high collision losses at this instant. Both of these mechanisms would be more effective, providing upward and forward impulses, with fore hind phases of less than 5%. a net increase in collisional energy losses. If the most life-like powering strategy, of returning lost energy directly after forefoot contact (red lines), is used, total collisional energy losses are reduced at low phases (H-F H-F H). The observed range of phases (grey bar in Fig. 4D), however, remains below those predicted by any of the collision models. Collision discussion It is clear that no walking animal is actually perfectly passive nor perfectly stiff-limbed. Equally, it is clear that there are never step changes in COM direction, and so there are not infinite forces, and energy losses calculated from a passive, stiff-limbed model should not be considered accurate. However, consideration of collisions, and especially their avoidance or potential amelioration, can provide insight into the selective pressures on both footfall timing [see Ruina et al. for horse galloping (Ruina et al., 5)] and mechanisms of powering [see Kuo for bipedal walking (Kuo, )] quadrupedal walking. Collisional energy losses in our example walking quadruped (Fig. 5) are minimised at a phase of ±5% an even spacing between each hindfoot and each forefoot placement. The reason behind this is twofold: first, the velocity at each collision is minimised if, when the front foot is being placed on the ground the hips are as high as possible and, when the hindleg is being placed on the ground, the shoulders are as high as possible. With this arrangement, achieved at phases of ±5%, the smallest possible proportion of mechanical energy is in the form of kinetic energy at each foot placement. Second, the deflection of the COM path at each foot placement is evenly divided; collision losses are reduced if the COM path is deflected by two intermediate changes rather than one large and one small (consider Equations 4 6). With our dogs, however, phases are approximately 1 17% (Table 1); in horses, the bias is also in this direction, accounting for their characteristic clipclop clip-clop sound. Note that this theme is not, however, universal (see Hildebrand, 1968) for walking quadrupeds. Let us first consider the effect of powering strategy given the observation that dogs (and horses) generally walk with a phase relationship of <5%. Fig. 5 suggests that the implications of realistic fore hind leg length and mass distribution have relatively little bearing on the take-home message apparent in the fore-aft symmetrical case (Fig. 5A). That is, at phases less than 5% there is a benefit in terms of a reduction in collision energy losses (for walking at a given speed) to the powering strategy displayed in red: energy lost at hindfoot collision should not be replaced immediately; rather, the energy lost because of both hind- and forefoot collisions should be replaced directly after forefoot placement. The reason for this is as follows: with this powering strategy, at lower phases the effect of the energy lost at hindfoot placement on the overall mean speed becomes small because a relatively brief part of the step is spent at this reduced energy state. Meanwhile, the energy, and so the speed of the COM, is reduced for the instant of front foot placement, thus reducing the collisional losses because of front foot contact. Interestingly, this timing of
8 54 J. R. Usherwood, S. B. Williams and A. M. Wilson mechanical energy loss and recovery is consistent with that observed in all our forceplate measurements. Let us next consider a potential selective pressure towards sub-5% phases from the phase described above as minimising collisional losses (5%). Here, we turn to the potential mechanisms for providing the required powering impulses. Kuo shows, for bipedal walking, some mechanisms of adding mechanical energy can be considerably more efficient than others (Kuo, ). In the bipedal case, powering with an ankle extension (presumably gastrocnemius action) late in stance may be four times less costly [than powering with a hip torque] because it decreases the collision loss at heel strike ; the collision geometry at foot placement can be smoothed by the lengthening of the trailing leg. We propose here two powering mechanisms with the potential for analogous path-smoothing benefits for quadrupeds (Fig. 6). Either a hip torque while the hindleg is early in stance or hindleg extension late in stance would contribute powering impulses with the concomitant effect of smoothing the COM path (deviating from the 4-bar linkage geometry) and reducing the collisional energy loss at front foot placement (the more significant collision because of the mass bias towards the front limbs, Fig. 5C,D). So, if quadrupeds habitually power locomotion with their hindlimbs [as suggested by their muscle anatomy, and supported for trotting by forceplate measurements (Lee et al., 1999)], then powering with either hip torques or leg extension would be effective in reducing collision costs, particularly at phases less than 5%. Whether collision mechanics might explain why many quadrupeds power locomotion with their hindlimbs, or the tendency for quadrupeds to have a mass bias towards the forelimbs, is beyond the scope of this study, but deserves further attention. We would like to recognise the contributions made by John Bertram and Russell Main during the development of this project, and thank John Hutchinson and two anonymous reviewers for their most helpful comments. This work was funded by the BBSRC. References Alexander, R. M. (1989). Optimization and gaits in the locomotion of vertebrates. Physiol. Rev. 69, Alexander, R. M. and Jayes, A. S. (1983). A dynamic similarity hypothesis for the gaits of quadrupedal mammals. J. Zool. Lond. 1, Cavagna, G. A. (1975). Force platforms as ergometers. J. Appl. Physiol. 39, Cavagna, G. A., Heglund, N. C. and Taylor, C. R. (1977). Mechanical work in terrestrial locomotion: two basic mechanisms for minimizing energy expenditure. Am. J. Physiol. 33, R43-R61. Collins, S., Ruina, A., Tedrake, R. and Wisse, M. (5). Efficient bipedal robots based on passive-dynamic walkers. Science 37, Donelan, J. M., Kram, R. and Kuo, A. D. (). Simultaneous positive and negative external mechanical work in human walking. J. Biomech. 35, Garcia, M., Chatterjee, A., Ruina, A. and Coleman, M. (1998). The simplest walking model: stability, complexity, and scaling. J. Biomech. Eng. 1, Griffin, T. M., Main, R. P. and Farley, C. T. (4). Biomechanics of quadrupedal walking: how do four-legged animals achieve inverted pendulum-like movements? J. Exp. Biol. 7, Hildebrand, M. (1968). Symmetrical gaits of dogs in relation to body build. J. Morphol. 14, Jayes, A. S. and Alexander, R. M. (1978). Mechanics of locomotion of dogs (Canis familiaris) and sheep (Ovis aries). J. Zool. Lond. 185, Kuo, A. D. (). Energetics of actively powered locomotion using the simplest walking model. J. Biomech. Eng. 14, Lee, D. V., Bertram, J. E. A. and Todhunter, R. J. (1999). Acceleration and balance in trotting dogs. J. Exp. Biol., McGeer, T. (199). Passive dynamic walking. Int. J. Robot. Res. 9, 6-8. Ortega, J. D. and Farley, C. T. (5). Minimizing center of mass vertical movement increases metabolic cost in walking. J. Appl. Physiol. 99, Ruina, A., Bertram, J. E. and Srinivasan, M. (5). A collisional model of the energetic cost of support work qualitatively explains leg sequencing in walking and galloping, pseudo-elastic leg behavior in running and the walkto-run transition. J. Theor. Biol. 14, Smith, A. C. and Berkemeir, M. D. (1997). Passive dynamic quadrupedal walking. Proceedings of the 1997 IEEE International Conference on Robotics and Automation Usherwood, J. R. (5). Why not walk faster? Biol. Lett. 1, Usherwood, J. R. and Bertram, J. E. A. (3). Understanding brachiation: insight from a collisional perspective. J. Exp. Biol. 6,
Biomechanics of quadrupedal walking: how do four-legged animals achieve inverted pendulum-like movements?
 The Journal of Experimental Biology 27, 3545-3558 Published by The Company of Biologists 24 doi:1.1242/jeb.1177 3545 Biomechanics of quadrupedal walking: how do four-legged animals achieve inverted pendulum-like
The Journal of Experimental Biology 27, 3545-3558 Published by The Company of Biologists 24 doi:1.1242/jeb.1177 3545 Biomechanics of quadrupedal walking: how do four-legged animals achieve inverted pendulum-like
Walking and Running BACKGROUND REVIEW. Planar Pendulum. BIO-39 October 30, From Oct. 25, Equation of motion (for small θ) Solution is
 Walking and Running BIO-39 October 30, 2018 BACKGROUND REVIEW From Oct. 25, 2018 Planar Pendulum Equation of motion (for small θ) 2 d g 0 2 dt Solution is Where: g is acceleration due to gravity l is pendulum
Walking and Running BIO-39 October 30, 2018 BACKGROUND REVIEW From Oct. 25, 2018 Planar Pendulum Equation of motion (for small θ) 2 d g 0 2 dt Solution is Where: g is acceleration due to gravity l is pendulum
-Elastic strain energy (duty factor decreases at higher speeds). Higher forces act on feet. More tendon stretch. More energy stored in tendon.
 As velocity increases ( ) (i.e. increasing Froude number v 2 / gl) the component of the energy cost of transport associated with: -Internal kinetic energy (limbs accelerated to higher angular velocity).
As velocity increases ( ) (i.e. increasing Froude number v 2 / gl) the component of the energy cost of transport associated with: -Internal kinetic energy (limbs accelerated to higher angular velocity).
(2) BIOMECHANICS of TERRESTRIAL LOCOMOTION
 (2) BIOMECHANICS of TERRESTRIAL LOCOMOTION Questions: - How does size influence the mode and speed of locomotion? - What determines the energy cost of locomotion? - Why do humans walk and run the way we
(2) BIOMECHANICS of TERRESTRIAL LOCOMOTION Questions: - How does size influence the mode and speed of locomotion? - What determines the energy cost of locomotion? - Why do humans walk and run the way we
Sample Solution for Problem 1.a
 Sample Solution for Problem 1.a 1 Inverted Pendulum Model (IPM) 1.1 Equations of Motion and Ground Reaction Forces Figure 1: Scheme of the Inverted Pendulum Model (IPM). The equations of motion of this
Sample Solution for Problem 1.a 1 Inverted Pendulum Model (IPM) 1.1 Equations of Motion and Ground Reaction Forces Figure 1: Scheme of the Inverted Pendulum Model (IPM). The equations of motion of this
Energetics of Actively Powered Locomotion Using the Simplest Walking Model
 Arthur D. Kuo Dept. of Mechanical Engineering and Applied Mechanics, University of Michigan, Ann Arbor, MI 48109-2125 email: artkuo@umich.edu Energetics of Actively Powered Locomotion Using the Simplest
Arthur D. Kuo Dept. of Mechanical Engineering and Applied Mechanics, University of Michigan, Ann Arbor, MI 48109-2125 email: artkuo@umich.edu Energetics of Actively Powered Locomotion Using the Simplest
RUNNING SPRINGS: SPEED AND ANIMAL SIZE
 J. exp. Biol. 185, 71 86 (1993) Printed in Great Britain The Company of Biologists Limited 1993 71 RUNNING SPRINGS: SPEED AND ANIMAL SIZE CLAIRE T. FARLEY 1, *, JAMES GLASHEEN 2 AND THOMAS A. MCMAHON 3
J. exp. Biol. 185, 71 86 (1993) Printed in Great Britain The Company of Biologists Limited 1993 71 RUNNING SPRINGS: SPEED AND ANIMAL SIZE CLAIRE T. FARLEY 1, *, JAMES GLASHEEN 2 AND THOMAS A. MCMAHON 3
Mechanical energy fluctuations during hill walking: the effects of slope on inverted pendulum exchange
 4895 The Journal of Experimental Biology 209, 4895-4900 Published by The Company of Biologists 2006 doi:10.1242/jeb.02584 Mechanical energy fluctuations during hill walking: the effects of slope on inverted
4895 The Journal of Experimental Biology 209, 4895-4900 Published by The Company of Biologists 2006 doi:10.1242/jeb.02584 Mechanical energy fluctuations during hill walking: the effects of slope on inverted
OPTIMAL TRAJECTORY GENERATION OF COMPASS-GAIT BIPED BASED ON PASSIVE DYNAMIC WALKING
 OPTIMAL TRAJECTORY GENERATION OF COMPASS-GAIT BIPED BASED ON PASSIVE DYNAMIC WALKING Minseung Kim Dept. of Computer Science Illinois Institute of Technology 3201 S. State St. Box 2082 Chicago IL 60616
OPTIMAL TRAJECTORY GENERATION OF COMPASS-GAIT BIPED BASED ON PASSIVE DYNAMIC WALKING Minseung Kim Dept. of Computer Science Illinois Institute of Technology 3201 S. State St. Box 2082 Chicago IL 60616
Body Stabilization of PDW toward Humanoid Walking
 Body Stabilization of PDW toward Humanoid Walking Masaki Haruna, Masaki Ogino, Koh Hosoda, Minoru Asada Dept. of Adaptive Machine Systems, Osaka University, Suita, Osaka, 565-0871, Japan ABSTRACT Passive
Body Stabilization of PDW toward Humanoid Walking Masaki Haruna, Masaki Ogino, Koh Hosoda, Minoru Asada Dept. of Adaptive Machine Systems, Osaka University, Suita, Osaka, 565-0871, Japan ABSTRACT Passive
Effects of Ankle Stiffness on Gait Selection of Dynamic Bipedal Walking with Flat Feet
 2 IEEE International Conference on Rehabilitation Robotics Rehab Week Zurich, ETH Zurich Science City, Switzerland, June 29 - July, 2 Effects of Ankle Stiffness on Gait Selection of Dynamic Bipedal Walking
2 IEEE International Conference on Rehabilitation Robotics Rehab Week Zurich, ETH Zurich Science City, Switzerland, June 29 - July, 2 Effects of Ankle Stiffness on Gait Selection of Dynamic Bipedal Walking
Toward a Human-like Biped Robot with Compliant Legs
 Book Title Book Editors IOS Press, 2003 1 Toward a Human-like Biped Robot with Compliant Legs Fumiya Iida a,b,1, Yohei Minekawa a Juergen Rummel a and Andre Seyfarth a a Locomotion Laboratory, University
Book Title Book Editors IOS Press, 2003 1 Toward a Human-like Biped Robot with Compliant Legs Fumiya Iida a,b,1, Yohei Minekawa a Juergen Rummel a and Andre Seyfarth a a Locomotion Laboratory, University
Biomechanics and Models of Locomotion
 Physics-Based Models for People Tracking: Biomechanics and Models of Locomotion Marcus Brubaker 1 Leonid Sigal 1,2 David J Fleet 1 1 University of Toronto 2 Disney Research, Pittsburgh Biomechanics Biomechanics
Physics-Based Models for People Tracking: Biomechanics and Models of Locomotion Marcus Brubaker 1 Leonid Sigal 1,2 David J Fleet 1 1 University of Toronto 2 Disney Research, Pittsburgh Biomechanics Biomechanics
Humanoid Robots and biped locomotion. Contact: Egidio Falotico
 Humanoid Robots and biped locomotion Contact: Egidio Falotico e.falotico@sssup.it Outline What is a Humanoid? Why Develop Humanoids? Challenges in Humanoid robotics Active vs Passive Locomotion Active
Humanoid Robots and biped locomotion Contact: Egidio Falotico e.falotico@sssup.it Outline What is a Humanoid? Why Develop Humanoids? Challenges in Humanoid robotics Active vs Passive Locomotion Active
The double contact phase in walking children
 The Journal of Experimental Biology 26, 2967-2978 23 The Company of Biologists Ltd doi:1.1242/jeb.494 2967 The double contact phase in walking children G. J. Bastien, N. C. Heglund and B. Schepens* Unité
The Journal of Experimental Biology 26, 2967-2978 23 The Company of Biologists Ltd doi:1.1242/jeb.494 2967 The double contact phase in walking children G. J. Bastien, N. C. Heglund and B. Schepens* Unité
Energetics Study of Mechanically Coupled Human Walking. Honors Undergraduate Thesis. the Undergraduate School of The Ohio State University
 Energetics Study of Mechanically Coupled Human Walking Honors Undergraduate Thesis Presented in partial fulfillment of the requirements for the degree Bachelor of Science in the Undergraduate School of
Energetics Study of Mechanically Coupled Human Walking Honors Undergraduate Thesis Presented in partial fulfillment of the requirements for the degree Bachelor of Science in the Undergraduate School of
Human Pose Tracking III: Dynamics. David Fleet University of Toronto
 Human Pose Tracking III: Dynamics David Fleet University of Toronto CIFAR Summer School, 2009 Interactions with the world are fundamental Implausible motions [Poon and Fleet, 01] Kinematic Model: damped
Human Pose Tracking III: Dynamics David Fleet University of Toronto CIFAR Summer School, 2009 Interactions with the world are fundamental Implausible motions [Poon and Fleet, 01] Kinematic Model: damped
Energetic Consequences of Walking Like an Inverted Pendulum: Step-to-Step Transitions
 ARTICLE Energetic Consequences of Walking Like an Inverted Pendulum: Step-to-Step Transitions Arthur D. Kuo, 1 J. Maxwell Donelan, 2 and Andy Ruina 3 1 Departments of Mechanical Engineering & Biomedical
ARTICLE Energetic Consequences of Walking Like an Inverted Pendulum: Step-to-Step Transitions Arthur D. Kuo, 1 J. Maxwell Donelan, 2 and Andy Ruina 3 1 Departments of Mechanical Engineering & Biomedical
MECHANICS OF LOCOMOTION IN LIZARDS
 The Journal of Experimental Biology 2, 2177 2188 (1997) Printed in Great Britain The Company of Biologists Limited 1997 JEB769 2177 MECHANICS OF LOCOMOTION IN LIZARDS CLAIRE T. FARLEY* AND T. CHRISTINE
The Journal of Experimental Biology 2, 2177 2188 (1997) Printed in Great Britain The Company of Biologists Limited 1997 JEB769 2177 MECHANICS OF LOCOMOTION IN LIZARDS CLAIRE T. FARLEY* AND T. CHRISTINE
THE OHIO JOURNAL OF SCIENCE
 THE OHIO JOURNAL OF SCIENCE Vol. 72 JULY, 1972 No. 4 BODY FORM AND GAIT IN TERRESTRIAL VERTEBRATES 1 WARREN F. WALKER, JR. Department of Biology, Oberlin College, Oberlin, Ohio 44074 One appeal of pure
THE OHIO JOURNAL OF SCIENCE Vol. 72 JULY, 1972 No. 4 BODY FORM AND GAIT IN TERRESTRIAL VERTEBRATES 1 WARREN F. WALKER, JR. Department of Biology, Oberlin College, Oberlin, Ohio 44074 One appeal of pure
Stable Upright Walking and Running using a simple Pendulum based Control Scheme
 1 Stable Upright Walking and Running using a simple Pendulum based Control Scheme H.-M. MAUS, J. RUMMEL and A. SEYFARTH Lauflabor Locomotion Laboratory, University of Jena, Germany E-mail: moritz.maus@uni-jena.de
1 Stable Upright Walking and Running using a simple Pendulum based Control Scheme H.-M. MAUS, J. RUMMEL and A. SEYFARTH Lauflabor Locomotion Laboratory, University of Jena, Germany E-mail: moritz.maus@uni-jena.de
An investigation of kinematic and kinetic variables for the description of prosthetic gait using the ENOCH system
 An investigation of kinematic and kinetic variables for the description of prosthetic gait using the ENOCH system K. OBERG and H. LANSHAMMAR* Amputee Training and Research Unit, University Hospital, Fack,
An investigation of kinematic and kinetic variables for the description of prosthetic gait using the ENOCH system K. OBERG and H. LANSHAMMAR* Amputee Training and Research Unit, University Hospital, Fack,
MECHANICS OF SIX-LEGGED RUNNERS
 J. exp. Biol. 14S, 129-146 (1990) 129 Printed in Great Britain The Company of Biologists Limited 1990 MECHANICS OF SIX-LEGGED RUNNERS BY ROBERT J. FULL AND MICHAEL S. TU Department of Zoology, University
J. exp. Biol. 14S, 129-146 (1990) 129 Printed in Great Britain The Company of Biologists Limited 1990 MECHANICS OF SIX-LEGGED RUNNERS BY ROBERT J. FULL AND MICHAEL S. TU Department of Zoology, University
Swing leg retraction helps biped walking stability
 Proceedings of 25 5th IEEE-RAS International Conference on Humanoid Robots Swing leg retraction helps biped walking stability M Wisse*, C G Atkeson,DKKloimwieder * Delft University of Technology, wwwdbltudelftnl,
Proceedings of 25 5th IEEE-RAS International Conference on Humanoid Robots Swing leg retraction helps biped walking stability M Wisse*, C G Atkeson,DKKloimwieder * Delft University of Technology, wwwdbltudelftnl,
Simultaneous positive and negative external mechanical work in human walking
 Journal of Biomechanics 35 (2002) 117 124 Simultaneous positive and negative external mechanical work in human walking J.Maxwell Donelan a, *, Rodger Kram a, Arthur D. Kuo b a Locomotion Laboratory, Department
Journal of Biomechanics 35 (2002) 117 124 Simultaneous positive and negative external mechanical work in human walking J.Maxwell Donelan a, *, Rodger Kram a, Arthur D. Kuo b a Locomotion Laboratory, Department
Putting Report Details: Key and Diagrams: This section provides a visual diagram of the. information is saved in the client s database
 Quintic Putting Report Information Guide Putting Report Details: Enter personal details of the client or individual who is being analysed; name, email address, date, mass, height and handicap. This information
Quintic Putting Report Information Guide Putting Report Details: Enter personal details of the client or individual who is being analysed; name, email address, date, mass, height and handicap. This information
Toward a Human-like Biped Robot with Compliant Legs
 Book Title Book Editors IOS Press, 23 1 Toward a Human-like Biped Robot with Compliant Legs Fumiya Iida a,b,1, Yohei Minekawa a Juergen Rummel a and Andre Seyfarth a a Locomotion Laboratory, University
Book Title Book Editors IOS Press, 23 1 Toward a Human-like Biped Robot with Compliant Legs Fumiya Iida a,b,1, Yohei Minekawa a Juergen Rummel a and Andre Seyfarth a a Locomotion Laboratory, University
Using GPOPS-II to optimize sum of squared torques of a double pendulum as a prosthesis leg. Abstract
 Using GPOPS-II to optimize sum of squared torques of a double pendulum as a prosthesis leg Abstract Milad Zarei MCE 593 Prosthesis Design & Control A two-dimensional, two links pendulum is developed to
Using GPOPS-II to optimize sum of squared torques of a double pendulum as a prosthesis leg Abstract Milad Zarei MCE 593 Prosthesis Design & Control A two-dimensional, two links pendulum is developed to
by Michael Young Human Performance Consulting
 by Michael Young Human Performance Consulting The high performance division of USATF commissioned research to determine what variables were most critical to success in the shot put The objective of the
by Michael Young Human Performance Consulting The high performance division of USATF commissioned research to determine what variables were most critical to success in the shot put The objective of the
Data-Informed Modeling of Milligram-Scale Quadrupedal Robot Locomotion
 Data-Informed Modeling of Milligram-Scale Quadrupedal Robot Locomotion Walker Gosrich, Ryan St. Pierre, and Sarah Bergbreiter Abstract This work uses the microquad, a quadrupedal, magnetically actuated
Data-Informed Modeling of Milligram-Scale Quadrupedal Robot Locomotion Walker Gosrich, Ryan St. Pierre, and Sarah Bergbreiter Abstract This work uses the microquad, a quadrupedal, magnetically actuated
INTERACTION OF STEP LENGTH AND STEP RATE DURING SPRINT RUNNING
 INTERACTION OF STEP LENGTH AND STEP RATE DURING SPRINT RUNNING Joseph P. Hunter 1, Robert N. Marshall 1,, and Peter J. McNair 3 1 Department of Sport and Exercise Science, The University of Auckland, Auckland,
INTERACTION OF STEP LENGTH AND STEP RATE DURING SPRINT RUNNING Joseph P. Hunter 1, Robert N. Marshall 1,, and Peter J. McNair 3 1 Department of Sport and Exercise Science, The University of Auckland, Auckland,
The validity of a rigid body model of a cricket ball-bat impact
 Available online at www.sciencedirect.com Procedia Engineering 34 (2012 ) 682 687 9 th Conference of the International Sports Engineering Association (ISEA) The validity of a rigid body model of a cricket
Available online at www.sciencedirect.com Procedia Engineering 34 (2012 ) 682 687 9 th Conference of the International Sports Engineering Association (ISEA) The validity of a rigid body model of a cricket
EXSC 408L Fall '03 Problem Set #2 Linear Motion. Linear Motion
 Problems: 1. Once you have recorded the calibration frame for a data collection, why is it important to make sure the camera does not shut off? hat happens if the camera automatically shuts off after being
Problems: 1. Once you have recorded the calibration frame for a data collection, why is it important to make sure the camera does not shut off? hat happens if the camera automatically shuts off after being
Supplementary Figure 1 An insect model based on Drosophila melanogaster. (a)
 Supplementary Figure 1 An insect model based on Drosophila melanogaster. (a) Side and ventral images of adult female flies used to calculate the sizes of body and leg segments. Scale bar is 0.3 mm. Green,
Supplementary Figure 1 An insect model based on Drosophila melanogaster. (a) Side and ventral images of adult female flies used to calculate the sizes of body and leg segments. Scale bar is 0.3 mm. Green,
Walking and running in the red-legged running frog, Kassina maculata
 The Journal of Experimental Biology 27, 399-41 Published by The Company of Biologists 24 doi:1.1242/jeb.761 399 Walking and running in the red-legged running frog, Kassina maculata A. N. Ahn*, E. Furrow
The Journal of Experimental Biology 27, 399-41 Published by The Company of Biologists 24 doi:1.1242/jeb.761 399 Walking and running in the red-legged running frog, Kassina maculata A. N. Ahn*, E. Furrow
Equine Cannon Angle System
 Equine Cannon System How to interpret the results December 2010 Page 1 of 14 Table of Contents Introduction... 3 The Sagittal Plane... 4 The Coronal Plane... 5 Results Format... 6 How to Interpret the
Equine Cannon System How to interpret the results December 2010 Page 1 of 14 Table of Contents Introduction... 3 The Sagittal Plane... 4 The Coronal Plane... 5 Results Format... 6 How to Interpret the
CHAPTER IV FINITE ELEMENT ANALYSIS OF THE KNEE JOINT WITHOUT A MEDICAL IMPLANT
 39 CHAPTER IV FINITE ELEMENT ANALYSIS OF THE KNEE JOINT WITHOUT A MEDICAL IMPLANT 4.1 Modeling in Biomechanics The human body, apart of all its other functions is a mechanical mechanism and a structure,
39 CHAPTER IV FINITE ELEMENT ANALYSIS OF THE KNEE JOINT WITHOUT A MEDICAL IMPLANT 4.1 Modeling in Biomechanics The human body, apart of all its other functions is a mechanical mechanism and a structure,
A New Approach to Modeling Vertical Stiffness in Heel-Toe Distance Runners
 Brigham Young University BYU ScholarsArchive All Faculty Publications 2003-12-01 A New Approach to Modeling Vertical Stiffness in Heel-Toe Distance Runners Iain Hunter iain_hunter@byu.edu Follow this and
Brigham Young University BYU ScholarsArchive All Faculty Publications 2003-12-01 A New Approach to Modeling Vertical Stiffness in Heel-Toe Distance Runners Iain Hunter iain_hunter@byu.edu Follow this and
Analysis of ankle kinetics and energy consumption with an advanced microprocessor controlled ankle foot prosthesis.
 Analysis of ankle kinetics and energy consumption with an advanced microprocessor controlled ankle foot prosthesis. D.Moser, N.Stech, J.McCarthy, G.Harris, S.Zahedi, A.McDougall Summary This study reports
Analysis of ankle kinetics and energy consumption with an advanced microprocessor controlled ankle foot prosthesis. D.Moser, N.Stech, J.McCarthy, G.Harris, S.Zahedi, A.McDougall Summary This study reports
Mobile Robots (Legged) (Take class notes)
 Mobile Robots (Legged) (Take class notes) Legged mobile robots Mobile robots are robots which can move There are two types of mobile robots - Legged two, four, six and eight legs - Wheeled one, two, three
Mobile Robots (Legged) (Take class notes) Legged mobile robots Mobile robots are robots which can move There are two types of mobile robots - Legged two, four, six and eight legs - Wheeled one, two, three
Ground reaction forces in horses trotting up an incline and on the level over a range of speeds
 The Journal of Experimental Biology 7, 357-35 Published by The Company of Biologists 4 doi:1./jeb.1171 357 Ground reaction forces in horses trotting up an incline and on the level over a range of speeds
The Journal of Experimental Biology 7, 357-35 Published by The Company of Biologists 4 doi:1./jeb.1171 357 Ground reaction forces in horses trotting up an incline and on the level over a range of speeds
Artifacts Due to Filtering Mismatch in Drop Landing Moment Data
 Camenga et al. UW-L Journal of Undergraduate Research XVI (213) Artifacts Due to Filtering Mismatch in Drop Landing Moment Data Elizabeth T. Camenga, Casey J. Rutten, Brendan D. Gould, Jillian T. Asmus,
Camenga et al. UW-L Journal of Undergraduate Research XVI (213) Artifacts Due to Filtering Mismatch in Drop Landing Moment Data Elizabeth T. Camenga, Casey J. Rutten, Brendan D. Gould, Jillian T. Asmus,
Stabilization of a Three-Dimensional Limit Cycle Walking Model through Step-to-Step Ankle Control
 2013 IEEE International Conference on Rehabilitation Robotics June 24-26, 2013 Seattle, Washington USA Stabilization of a Three-Dimensional Limit Cycle Walking Model through Step-to-Step Ankle Control
2013 IEEE International Conference on Rehabilitation Robotics June 24-26, 2013 Seattle, Washington USA Stabilization of a Three-Dimensional Limit Cycle Walking Model through Step-to-Step Ankle Control
Biomechanics of locomotion in Asian elephants
 694 The Journal of Experimental Biology 3, 694-76. Published by The Company of Biologists Ltd doi:.4/jeb.35436 Biomechanics of locomotion in Asian elephants J. J. Genin, P. A. Willems, G. A. Cavagna, R.
694 The Journal of Experimental Biology 3, 694-76. Published by The Company of Biologists Ltd doi:.4/jeb.35436 Biomechanics of locomotion in Asian elephants J. J. Genin, P. A. Willems, G. A. Cavagna, R.
Dynamically stepping over large obstacle utilizing PSO optimization in the B4LC system
 1 Dynamically stepping over large obstacle utilizing PSO optimization in the B4LC system QI LIU, JIE ZHAO, KARSTEN BERNS Robotics Research Lab, University of Kaiserslautern, Kaiserslautern, 67655, Germany
1 Dynamically stepping over large obstacle utilizing PSO optimization in the B4LC system QI LIU, JIE ZHAO, KARSTEN BERNS Robotics Research Lab, University of Kaiserslautern, Kaiserslautern, 67655, Germany
THE ROLE OF COMPLIANCE IN MAMMALIAN RUNNING GAITS
 J. exp. Biol. 115, 263-282 (1985) 263 Printed in Gnat Britain The Company of Biologists Limited 1985 THE ROLE OF COMPLIANCE IN MAMMALIAN RUNNING GAITS BY T. A. M C M A H O N Division of Applied Sciences,
J. exp. Biol. 115, 263-282 (1985) 263 Printed in Gnat Britain The Company of Biologists Limited 1985 THE ROLE OF COMPLIANCE IN MAMMALIAN RUNNING GAITS BY T. A. M C M A H O N Division of Applied Sciences,
Sprinting: A Biomechanical Approach By Tom Tellez
 Sprinting: A Biomechanical Approach By Tom Tellez World class male sprinters stride approximately forty-three times for a 100 meter race. If a mechanical error costs one-one thousandth of a second per
Sprinting: A Biomechanical Approach By Tom Tellez World class male sprinters stride approximately forty-three times for a 100 meter race. If a mechanical error costs one-one thousandth of a second per
In memory of Dr. Kevin P. Granata, my graduate advisor, who was killed protecting others on the morning of April 16, 2007.
 Acknowledgement In memory of Dr. Kevin P. Granata, my graduate advisor, who was killed protecting others on the morning of April 16, 2007. There are many others without whom I could not have completed
Acknowledgement In memory of Dr. Kevin P. Granata, my graduate advisor, who was killed protecting others on the morning of April 16, 2007. There are many others without whom I could not have completed
Controlling Walking Behavior of Passive Dynamic Walker utilizing Passive Joint Compliance
 Controlling Walking Behavior of Passive Dynamic Walker utilizing Passive Joint Compliance Takashi TAKUMA, Koh HOSODA Department of Adaptive Machine Systems, Graduate School of Engineering Osaka University
Controlling Walking Behavior of Passive Dynamic Walker utilizing Passive Joint Compliance Takashi TAKUMA, Koh HOSODA Department of Adaptive Machine Systems, Graduate School of Engineering Osaka University
RESEARCH ARTICLE Biomechanics of human bipedal gallop: asymmetry dictates leg function
 8 The Journal of Experimental Biology 6, 8-9. Published by The Company of Biologists Ltd doi:./jeb.769 RESEARCH ARTICLE Biomechanics of human bipedal gallop: asymmetry dictates leg function Pieter Fiers,,
8 The Journal of Experimental Biology 6, 8-9. Published by The Company of Biologists Ltd doi:./jeb.769 RESEARCH ARTICLE Biomechanics of human bipedal gallop: asymmetry dictates leg function Pieter Fiers,,
John Sushko. Major Professor: Kyle B. Reed, Ph.D. Rajiv Dubey, Ph.D. Jose Porteiro, Ph.D. Date of Approval: October 21, 2011
 Asymmetric Passive Dynamic Walker Used to Examine Gait Rehabilitation Methods by John Sushko A thesis submitted in partial fulfillment of the requirements for the degree of Master of Science Department
Asymmetric Passive Dynamic Walker Used to Examine Gait Rehabilitation Methods by John Sushko A thesis submitted in partial fulfillment of the requirements for the degree of Master of Science Department
Mechanics of Legged Locomotion. Running. Dr Dan Dudek
 Mechanics of Legged Locomotion Running Dr Dan Dudek North Cross School dmdudek@northcross.org https://sites.google.com/a/northcross.org/dr-dan-dudek/ 1 Wheel Hypothesis Sir James Gray 2 BioWheel? Stomatopod
Mechanics of Legged Locomotion Running Dr Dan Dudek North Cross School dmdudek@northcross.org https://sites.google.com/a/northcross.org/dr-dan-dudek/ 1 Wheel Hypothesis Sir James Gray 2 BioWheel? Stomatopod
THE INITIAL STAGE THE FINAL STAGE
 THE JAVELIN RUN-UP By Hans Torim A detailed description of the author s views on the javelin run-up from the initial stages to the impulse stride and the pre-delivery position. The article is a slightly
THE JAVELIN RUN-UP By Hans Torim A detailed description of the author s views on the javelin run-up from the initial stages to the impulse stride and the pre-delivery position. The article is a slightly
Current issues regarding induced acceleration analysis of walking using the integration method to decompose the GRF
 Current issues regarding induced acceleration analysis of walking using the integration method to decompose the GRF George Chen May 17, 2002 Stanford Neuromuscular Biomechanics Lab Group Muscle contribution
Current issues regarding induced acceleration analysis of walking using the integration method to decompose the GRF George Chen May 17, 2002 Stanford Neuromuscular Biomechanics Lab Group Muscle contribution
Variable Face Milling to Normalize Putter Ball Speed and Maximize Forgiveness
 Proceedings Variable Face Milling to Normalize Putter Ball Speed and Maximize Forgiveness Jacob Lambeth *, Dustin Brekke and Jeff Brunski Cleveland Golf, 5601 Skylab Rd. Huntington Beach, CA 92647, USA;
Proceedings Variable Face Milling to Normalize Putter Ball Speed and Maximize Forgiveness Jacob Lambeth *, Dustin Brekke and Jeff Brunski Cleveland Golf, 5601 Skylab Rd. Huntington Beach, CA 92647, USA;
Biomechanics Sample Problems
 Biomechanics Sample Problems Forces 1) A 90 kg ice hockey player collides head on with an 80 kg ice hockey player. If the first person exerts a force of 450 N on the second player, how much force does
Biomechanics Sample Problems Forces 1) A 90 kg ice hockey player collides head on with an 80 kg ice hockey player. If the first person exerts a force of 450 N on the second player, how much force does
Steffen Willwacher, Katina Fischer, Gert Peter Brüggemann Institute of Biomechanics and Orthopaedics, German Sport University, Cologne, Germany
 P01-3 ID126 SURFACE STIFFNESS AFFECTS JOINT LOADING IN RUNNING Steffen Willwacher, Katina Fischer, Gert Peter Brüggemann Institute of Biomechanics and Orthopaedics, German Sport University, Cologne, Germany
P01-3 ID126 SURFACE STIFFNESS AFFECTS JOINT LOADING IN RUNNING Steffen Willwacher, Katina Fischer, Gert Peter Brüggemann Institute of Biomechanics and Orthopaedics, German Sport University, Cologne, Germany
SIMULTANEOUS RECORDINGS OF VELOCITY AND VIDEO DURING SWIMMING
 Portuguese Journal of Sport Sciences. 6:supl. 2, 32-35, 2006 SIMULTANEOUS RECORDINGS OF VELOCITY AND VIDEO DURING SWIMMING Albert B. Craig 1, Budd Termin2, and David R. Pendergast 2 1University of Rochester,
Portuguese Journal of Sport Sciences. 6:supl. 2, 32-35, 2006 SIMULTANEOUS RECORDINGS OF VELOCITY AND VIDEO DURING SWIMMING Albert B. Craig 1, Budd Termin2, and David R. Pendergast 2 1University of Rochester,
Gait Analysis of a Little Biped Robot. Received May 2015; accepted July 2015
 ICIC Express Letters Part B: Applications ICIC International c216 ISSN 2185-2766 Volume 7, Number 5, May 216 pp. 1 6 Gait Analysis of a Little Biped Robot Chi-Sheng Tsai 1, Chen-Huei Hsieh 1, Wenning QIU
ICIC Express Letters Part B: Applications ICIC International c216 ISSN 2185-2766 Volume 7, Number 5, May 216 pp. 1 6 Gait Analysis of a Little Biped Robot Chi-Sheng Tsai 1, Chen-Huei Hsieh 1, Wenning QIU
Foot Placement in the Simplest Slope Walker Reveals a Wide Range of Walking Solutions
 Foot Placement in the Simplest Slope Walker Reveals a Wide Range of Walking Solutions Pranav A. Bhounsule Abstract We show that the simplest slope walker can walk over wide combinations of step lengths
Foot Placement in the Simplest Slope Walker Reveals a Wide Range of Walking Solutions Pranav A. Bhounsule Abstract We show that the simplest slope walker can walk over wide combinations of step lengths
DETC DESIGN OPTIMIZATION OF A NOVEL TRIPEDAL LOCOMOTION ROBOT THROUGH SIMULATION AND EXPERIMENTS FOR A SINGLE STEP DYNAMIC GAIT
 Proceedings of the ASME 27 International Design Engineering Technical Conferences & Computers and Information in Engineering Conference IDETC/CIE 27 September 4-7, 27, Las Vegas, Nevada, USA DETC27-34472
Proceedings of the ASME 27 International Design Engineering Technical Conferences & Computers and Information in Engineering Conference IDETC/CIE 27 September 4-7, 27, Las Vegas, Nevada, USA DETC27-34472
MECHANICS OF A RAPID RUNNING INSECT: TWO-, FOUR- AND SEX-LEGGED LOCOMOTION
 J. exp. Biol. 156, 215-231 (1991) 2 1 5 Printed in Great Britain The Company of Biologists Limited 1991 MECHANICS OF A RAPID RUNNING INSECT: TWO-, FOUR- AND SEX-LEGGED LOCOMOTION BY ROBERT J. FULL AND
J. exp. Biol. 156, 215-231 (1991) 2 1 5 Printed in Great Britain The Company of Biologists Limited 1991 MECHANICS OF A RAPID RUNNING INSECT: TWO-, FOUR- AND SEX-LEGGED LOCOMOTION BY ROBERT J. FULL AND
Impact Points and Their Effect on Trajectory in Soccer
 Proceedings Impact Points and Their Effect on Trajectory in Soccer Kaoru Kimachi 1, *, Sungchan Hong 2, Shuji Shimonagata 3 and Takeshi Asai 2 1 Doctoral Program of Coaching Science, University of Tsukuba,
Proceedings Impact Points and Their Effect on Trajectory in Soccer Kaoru Kimachi 1, *, Sungchan Hong 2, Shuji Shimonagata 3 and Takeshi Asai 2 1 Doctoral Program of Coaching Science, University of Tsukuba,
Journal of Chemical and Pharmaceutical Research, 2016, 8(6): Research Article. Walking Robot Stability Based on Inverted Pendulum Model
 Available online www.jocpr.com Journal of Chemical and Pharmaceutical Research, 2016, 8(6):463-467 Research Article ISSN : 0975-7384 CODEN(USA) : JCPRC5 Walking Robot Stability Based on Inverted Pendulum
Available online www.jocpr.com Journal of Chemical and Pharmaceutical Research, 2016, 8(6):463-467 Research Article ISSN : 0975-7384 CODEN(USA) : JCPRC5 Walking Robot Stability Based on Inverted Pendulum
+ t1 t2 moment-time curves
 Part 6 - Angular Kinematics / Angular Impulse 1. While jumping over a hurdle, an athlete s hip angle was measured to be 2.41 radians. Within 0.15 seconds, the hurdler s hip angle changed to be 3.29 radians.
Part 6 - Angular Kinematics / Angular Impulse 1. While jumping over a hurdle, an athlete s hip angle was measured to be 2.41 radians. Within 0.15 seconds, the hurdler s hip angle changed to be 3.29 radians.
Gyro stabilized biped walking
 Gyro stabilized biped walking N. Michael Mayer Asada S.I. Project, ERATO JST Osaka, Japan Email: michael@jeap.org Kazuhiro Masui Osaka University, Osaka, Japan Email: masui@jeap.org Matthew Browne CSIRO
Gyro stabilized biped walking N. Michael Mayer Asada S.I. Project, ERATO JST Osaka, Japan Email: michael@jeap.org Kazuhiro Masui Osaka University, Osaka, Japan Email: masui@jeap.org Matthew Browne CSIRO
Each copy of any part of a JSTOR transmission must contain the same copyright notice that appears on the screen or printed page of such transmission.
 Walking and Running Author(s): R. McNeill Alexander Source: The Mathematical Gazette, Vol. 80, No. 488 (Jul., 1996), pp. 262-266 Published by: The Mathematical Association Stable URL: http://www.jstor.org/stable/3619558
Walking and Running Author(s): R. McNeill Alexander Source: The Mathematical Gazette, Vol. 80, No. 488 (Jul., 1996), pp. 262-266 Published by: The Mathematical Association Stable URL: http://www.jstor.org/stable/3619558
A Bio-inspired Behavior Based Bipedal Locomotion Control B4LC Method for Bipedal Upslope Walking
 1 A Bio-inspired Behavior Based Bipedal Locomotion Control B4LC Method for Bipedal Upslope Walking JIE ZHAO, QI LIU, STEFFEN SCHUETZ, and KARSTEN BERNS Robotics Research Lab, University of Kaiserslautern,
1 A Bio-inspired Behavior Based Bipedal Locomotion Control B4LC Method for Bipedal Upslope Walking JIE ZHAO, QI LIU, STEFFEN SCHUETZ, and KARSTEN BERNS Robotics Research Lab, University of Kaiserslautern,
Mechanical work and muscular efficiency in walking children
 The Journal of Experimental Biology 7, 587-59 Published by The Company of Biologists doi:/jeb79 587 Mechanical work and muscular efficiency in walking children B Schepens, G J Bastien, N C Heglund and
The Journal of Experimental Biology 7, 587-59 Published by The Company of Biologists doi:/jeb79 587 Mechanical work and muscular efficiency in walking children B Schepens, G J Bastien, N C Heglund and
Development of a Simulation Model for Swimming with Diving Fins
 Proceedings Development of a Simulation Model for Swimming with Diving Fins Motomu Nakashima 1, *, Yosuke Tanno 2, Takashi Fujimoto 3 and Yutaka Masutani 3 1 Department of Systems and Control Engineering,
Proceedings Development of a Simulation Model for Swimming with Diving Fins Motomu Nakashima 1, *, Yosuke Tanno 2, Takashi Fujimoto 3 and Yutaka Masutani 3 1 Department of Systems and Control Engineering,
REPORT DOCUMENTATION PAGE
 REPORT DOCUMENTATION PAGE Form Approved OMB NO. 0704-0188 The public reporting burden for this collection of information is estimated to average 1 hour per response, including the time for reviewing instructions,
REPORT DOCUMENTATION PAGE Form Approved OMB NO. 0704-0188 The public reporting burden for this collection of information is estimated to average 1 hour per response, including the time for reviewing instructions,
How Do You Swing? You should be working with new lab partners starting with this lab.
 You should be working with new lab partners starting with this lab. Exploration: Swinging your arms and legs back and forth Discuss and try out the following questions within your lab group. After you
You should be working with new lab partners starting with this lab. Exploration: Swinging your arms and legs back and forth Discuss and try out the following questions within your lab group. After you
From Passive to Active Dynamic 3D Bipedal Walking - An Evolutionary Approach -
 From Passive to Active Dynamic 3D Bipedal Walking - An Evolutionary Approach - Steffen Wischmann and Frank Pasemann Fraunhofer Institute for Autonomous Intelligent Systems (AiS) Schloss Birlinghoven, 53754
From Passive to Active Dynamic 3D Bipedal Walking - An Evolutionary Approach - Steffen Wischmann and Frank Pasemann Fraunhofer Institute for Autonomous Intelligent Systems (AiS) Schloss Birlinghoven, 53754
Gait Analysis of Wittenberg s Women s Basketball Team: The Relationship between Shoulder Movement and Injuries
 Gait Analysis of Wittenberg s Women s Basketball Team: The Relationship between Shoulder Movement and Injuries Katie Bondy Senior Presentation May 1 st 2013 Research Question Among basketball players,
Gait Analysis of Wittenberg s Women s Basketball Team: The Relationship between Shoulder Movement and Injuries Katie Bondy Senior Presentation May 1 st 2013 Research Question Among basketball players,
Supplementary Figure S1
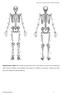 Supplementary Figure S1: Anterior and posterior views of the marker set used in the running gait trials. Forty-six markers were attached to the subject (15 markers on each leg, 4 markers on each arm, and
Supplementary Figure S1: Anterior and posterior views of the marker set used in the running gait trials. Forty-six markers were attached to the subject (15 markers on each leg, 4 markers on each arm, and
ZMP Trajectory Generation for Reduced Trunk Motions of Biped Robots
 ZMP Trajectory Generation for Reduced Trunk Motions of Biped Robots Jong H. Park School of Mechanical Engineering Hanyang University Seoul, 33-79, Korea email:jong.park@ieee.org Yong K. Rhee School of
ZMP Trajectory Generation for Reduced Trunk Motions of Biped Robots Jong H. Park School of Mechanical Engineering Hanyang University Seoul, 33-79, Korea email:jong.park@ieee.org Yong K. Rhee School of
Walking with coffee: when and why coffee spills
 Walking with coffee: when and why coffee spills Hans C. Mayer and Rouslan Krechetnikov Department of Mechanical Engineering University of California at Santa Barbara February 20-24, 2012 Page 1/25 Motivation
Walking with coffee: when and why coffee spills Hans C. Mayer and Rouslan Krechetnikov Department of Mechanical Engineering University of California at Santa Barbara February 20-24, 2012 Page 1/25 Motivation
Perry Issue: Gait Rehab
 Perry Issue: Gait Rehab Dynamic Principles of Gait and Their Clinical Implications Arthur D. Kuo, J. Maxwell Donelan A healthy gait pattern depends on an array of biomechanical features, orchestrated by
Perry Issue: Gait Rehab Dynamic Principles of Gait and Their Clinical Implications Arthur D. Kuo, J. Maxwell Donelan A healthy gait pattern depends on an array of biomechanical features, orchestrated by
Kinematic Differences between Set- and Jump-Shot Motions in Basketball
 Proceedings Kinematic Differences between Set- and Jump-Shot Motions in Basketball Hiroki Okubo 1, * and Mont Hubbard 2 1 Department of Advanced Robotics, Chiba Institute of Technology, 2-17-1 Tsudanuma,
Proceedings Kinematic Differences between Set- and Jump-Shot Motions in Basketball Hiroki Okubo 1, * and Mont Hubbard 2 1 Department of Advanced Robotics, Chiba Institute of Technology, 2-17-1 Tsudanuma,
 Kochi University of Technology Aca Study on Dynamic Analysis and Wea Title stem for Golf Swing Author(s) LI, Zhiwei Citation 高知工科大学, 博士論文. Date of 2015-03 issue URL http://hdl.handle.net/10173/1281 Rights
Kochi University of Technology Aca Study on Dynamic Analysis and Wea Title stem for Golf Swing Author(s) LI, Zhiwei Citation 高知工科大学, 博士論文. Date of 2015-03 issue URL http://hdl.handle.net/10173/1281 Rights
Motion Control of a Bipedal Walking Robot
 Motion Control of a Bipedal Walking Robot Lai Wei Ying, Tang Howe Hing, Mohamed bin Hussein Faculty of Mechanical Engineering Universiti Teknologi Malaysia, 81310 UTM Skudai, Johor, Malaysia. Wylai2@live.my
Motion Control of a Bipedal Walking Robot Lai Wei Ying, Tang Howe Hing, Mohamed bin Hussein Faculty of Mechanical Engineering Universiti Teknologi Malaysia, 81310 UTM Skudai, Johor, Malaysia. Wylai2@live.my
Gait. Kinesiology RHS 341 Lecture 12 Dr. Einas Al-Eisa
 Gait Kinesiology RHS 341 Lecture 12 Dr. Einas Al-Eisa Definitions Locomotion = the act of moving from one place to the other Gait = the manner of walking Definitions Walking = a smooth, highly coordinated,
Gait Kinesiology RHS 341 Lecture 12 Dr. Einas Al-Eisa Definitions Locomotion = the act of moving from one place to the other Gait = the manner of walking Definitions Walking = a smooth, highly coordinated,
Equation 1: F spring = kx. Where F is the force of the spring, k is the spring constant and x is the displacement of the spring. Equation 2: F = mg
 1 Introduction Relationship between Spring Constant and Length of Bungee Cord In this experiment, we aimed to model the behavior of the bungee cord that will be used in the Bungee Challenge. Specifically,
1 Introduction Relationship between Spring Constant and Length of Bungee Cord In this experiment, we aimed to model the behavior of the bungee cord that will be used in the Bungee Challenge. Specifically,
Megan E. Krause, BSBSE, Young Hui Chang, Ph.D. Comparative Neuromechanics Laboratory. Georgia Institute of Technology
 Megan E. Krause, BSBSE, Young Hui Chang, Ph.D. Comparative Neuromechanics Laboratory Sh School of Applied Physiology Georgia Institute of Technology 1 Variety of ankle constraints during locomotion: Fashion
Megan E. Krause, BSBSE, Young Hui Chang, Ph.D. Comparative Neuromechanics Laboratory Sh School of Applied Physiology Georgia Institute of Technology 1 Variety of ankle constraints during locomotion: Fashion
Robots With Legs. Helge Wrede
 Robots With Legs Helge Wrede 27.11.2017 Outline Motivation Overview Properties Number of legs Balance Walking Basic Bipedal Implementation Dynamic Balancing Concepts 3D-LIPM 2 Motivation Figure: Side view
Robots With Legs Helge Wrede 27.11.2017 Outline Motivation Overview Properties Number of legs Balance Walking Basic Bipedal Implementation Dynamic Balancing Concepts 3D-LIPM 2 Motivation Figure: Side view
Toward a human-like biped robot with compliant legs
 Robotics and Autonomous Systems ( ) www.elsevier.com/locate/robot Toward a human-like biped robot with compliant legs Fumiya Iida a,b,c,, Yohei Minekawa a, Jürgen Rummel a, André Seyfarth a a Locomotion
Robotics and Autonomous Systems ( ) www.elsevier.com/locate/robot Toward a human-like biped robot with compliant legs Fumiya Iida a,b,c,, Yohei Minekawa a, Jürgen Rummel a, André Seyfarth a a Locomotion
RESEARCH ARTICLE Energetically optimal stride frequency in running: the effects of incline and decline
 289 The Journal of Experimental Biology 214, 289-295 211. Published by The Company of Biologists Ltd doi:1.1242/jeb.53157 RESEARCH ARTICLE Energetically optimal stride frequency in running: the effects
289 The Journal of Experimental Biology 214, 289-295 211. Published by The Company of Biologists Ltd doi:1.1242/jeb.53157 RESEARCH ARTICLE Energetically optimal stride frequency in running: the effects
Limit Cycle Walking and Running of Biped Robots
 Tokyo Institute of Technology Yamakita Lab. Limit Cycle Walking and Running of Biped Robots Masaki Yamakita Tokyo Institute of Technology Introduction of Yamakita Lab. 1/14 Other Research Topics State
Tokyo Institute of Technology Yamakita Lab. Limit Cycle Walking and Running of Biped Robots Masaki Yamakita Tokyo Institute of Technology Introduction of Yamakita Lab. 1/14 Other Research Topics State
STABILITY AND CHAOS IN PASSIVE-DYNAMIC LOCOMOTION
 STABILITY AND CHAOS IN PASSIVE-DYNAMIC LOCOMOTION M.J. COLEMAN, M. GARCIA, A. L. RUINA AND J. S. CAMP Department of Theoretical and Applied Mechanics Cornell University, Ithaca, NY 14853-751 AND A. CHATTERJEE
STABILITY AND CHAOS IN PASSIVE-DYNAMIC LOCOMOTION M.J. COLEMAN, M. GARCIA, A. L. RUINA AND J. S. CAMP Department of Theoretical and Applied Mechanics Cornell University, Ithaca, NY 14853-751 AND A. CHATTERJEE
Colin Jackson's Hurdle Clearance Technique
 Colin Jackson's Hurdle Clearance Technique By Milan Čoh, Biomechanical Laboratory, Faculty of Sport, University of Ljubljana, Slovenia INTRODUCTION Colin Jackson is, uncontestedly, one of the greatest
Colin Jackson's Hurdle Clearance Technique By Milan Čoh, Biomechanical Laboratory, Faculty of Sport, University of Ljubljana, Slovenia INTRODUCTION Colin Jackson is, uncontestedly, one of the greatest
ITF Coaches Education Programme Biomechanics of the forehand stroke
 ITF Coaches Education Programme Biomechanics of the forehand stroke Original article: Bahamonde, R. (2001). ITF CSSR, 24, 6-8 Introduction The tennis forehand stroke has changed drastically over the last
ITF Coaches Education Programme Biomechanics of the forehand stroke Original article: Bahamonde, R. (2001). ITF CSSR, 24, 6-8 Introduction The tennis forehand stroke has changed drastically over the last
Learning Energy Efficient Walking Based on Ballistics
 Learning Energy Efficient Walking Based on Ballistics Masaki Ogino, Koh Hosoda and Minoru Asada Dept. of Adaptive Machine Systems, Graduate School of Engineering,, HANDAI Frontier Research Center ogino@er.ams.eng.osaka-u.ac.jp,
Learning Energy Efficient Walking Based on Ballistics Masaki Ogino, Koh Hosoda and Minoru Asada Dept. of Adaptive Machine Systems, Graduate School of Engineering,, HANDAI Frontier Research Center ogino@er.ams.eng.osaka-u.ac.jp,
First Hops of the 3D Bow Leg
 First Hops of the 3D Bow Leg Garth Zeglin and H. Benjamin Brown, Jr. Robotics Institute Carnegie Mellon University Pittsburgh, PA 15213, USA ABSTRACT We have constructed several hopping machines using
First Hops of the 3D Bow Leg Garth Zeglin and H. Benjamin Brown, Jr. Robotics Institute Carnegie Mellon University Pittsburgh, PA 15213, USA ABSTRACT We have constructed several hopping machines using
Using sensory feedback to improve locomotion performance of the salamander robot in different environments
 Using sensory feedback to improve locomotion performance of the salamander robot in different environments João Lourenço Silvério Assistant: Jérémie Knüsel Structure of the presentation: I. Overview II.
Using sensory feedback to improve locomotion performance of the salamander robot in different environments João Lourenço Silvério Assistant: Jérémie Knüsel Structure of the presentation: I. Overview II.
The Starting Point. Prosthetic Alignment in the Transtibial Amputee. Outline. COM Motion in the Coronal Plane
 Prosthetic Alignment in the Transtibial Amputee The Starting Point David C. Morgenroth, MD, Department of Rehabilitation Medicine University of Washington VAPSHCS Outline COM Motion in the Coronal Plane
Prosthetic Alignment in the Transtibial Amputee The Starting Point David C. Morgenroth, MD, Department of Rehabilitation Medicine University of Washington VAPSHCS Outline COM Motion in the Coronal Plane
A NEW GOLF-SWING ROBOT MODEL UTILIZING SHAFT ELASTICITY
 Journal of Sound and Vibration (1998) 17(1), 17 31 Article No. sv981733 A NEW GOLF-SWING ROBOT MODEL UTILIZING SHAFT ELASTICITY S. SUZUKI Department of Mechanical System Engineering, Kitami Institute of
Journal of Sound and Vibration (1998) 17(1), 17 31 Article No. sv981733 A NEW GOLF-SWING ROBOT MODEL UTILIZING SHAFT ELASTICITY S. SUZUKI Department of Mechanical System Engineering, Kitami Institute of
Biomechanics analysis of human walking with load carriage
 Technology and Health Care 23 (2015) S567 S575 DOI 10.3233/THC-150995 IOS Press S567 Biomechanics analysis of human walking with load carriage Xiuxia Yang, Guorong Zhao, Di Liu, Weiei Zhou and Hewei Zhao
Technology and Health Care 23 (2015) S567 S575 DOI 10.3233/THC-150995 IOS Press S567 Biomechanics analysis of human walking with load carriage Xiuxia Yang, Guorong Zhao, Di Liu, Weiei Zhou and Hewei Zhao
Prelab for the Ballistic Pendulum
 Ballistic Pendulum 1 Prelab for the Ballistic Pendulum 1. Write the general horizontal and vertical motion Kinematics equations for a horizontally launched projectile. 2. Write the relevant Conservation
Ballistic Pendulum 1 Prelab for the Ballistic Pendulum 1. Write the general horizontal and vertical motion Kinematics equations for a horizontally launched projectile. 2. Write the relevant Conservation
Gait analysis for the development of the biped robot foot structure
 Preprints of the 9th World Congress The International Federation of Automatic Control Cape Town, South Africa. August 4-9, 4 Gait analysis for the development of the biped robot foot structure Yusuke OGAWA
Preprints of the 9th World Congress The International Federation of Automatic Control Cape Town, South Africa. August 4-9, 4 Gait analysis for the development of the biped robot foot structure Yusuke OGAWA
3D Limit Cycle Walking of Musculoskeletal Humanoid Robot with Flat Feet
 The 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems October 11-15, 2009 St. Louis, USA 3D Limit Cycle Walking of Musculoskeletal Humanoid Robot with Flat Feet Kenichi Narioka,
The 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems October 11-15, 2009 St. Louis, USA 3D Limit Cycle Walking of Musculoskeletal Humanoid Robot with Flat Feet Kenichi Narioka,
