Control and Function of Arm Swing in Human Walking and Running
|
|
|
- Owen Barnett
- 6 years ago
- Views:
Transcription
1 Control and Function of Arm Swing in Human Walking and Running The Harvard community has made this article openly available. Please share how this access benefits you. Your story matters. Citation Published Version Accessed Citable Link Terms of Use Pontzer, Herman, John H. Holloway III, David A. Raichlen, and Daniel E. Lieberman. 29. Control and function of arm swing in human walking and running. Journal of Experimental Biology 22: doi:.22/jeb.2927 December, 27 5:5:25 PM EST This article was downloaded from Harvard University's DASH repository, and is made available under the terms and conditions applicable to Other Posted Material, as set forth at (Article begins on next page)
2 523 The Journal of Experimental Biology 22, Published by The Company of Biologists 29 doi:.22/jeb.2927 Control and function of arm swing in human walking and running Herman Pontzer, *, John H. Holloway 3rd, David A. Raichlen 2 and Daniel E. Lieberman 3 Department of Anthropology, Washington University, 9 McMillan Hall, Saint Louis, MO 633, USA, 2 Department of Anthropology, University of Arizona, 9 E. South Campus Drive, PO Box 23, Tucson, AZ 8572, USA and 3 Department of Anthropology, Harvard University, Divinity Avenue, Cambridge, MA 238, USA *Author for correspondence ( hpontzer@artsci.wustl.edu) Accepted 9 November 28 SUMMARY We investigated the control and function of arm swing in human walking and running to test the hypothesis that the arms act as passive mass dampers powered by movement of the lower body, rather than being actively driven by the shoulder muscles. We measured locomotor cost, deltoid muscle activity and kinematics in healthy adult subjects while walking and running on a treadmill in three experimental conditions: control; no arms (arms folded across the chest); and arm weights (weights worn at the elbow). Decreasing and increasing the moment of inertia of the upper body in no arms and arm weights conditions, respectively, had corresponding effects on head yaw and on the phase differences between shoulder and pelvis rotation, consistent with the view of arms as mass dampers. Angular acceleration of the shoulders and arm increased with torsion of the trunk and shoulder, respectively, but angular acceleration of the shoulders was not inversely related to angular acceleration of the pelvis or arm. Restricting arm swing in no arms trials had no effect on locomotor cost. Anterior and posterior portions of the deltoid contracted simultaneously rather than firing alternately to drive the arm. These results support a passive arm swing hypothesis for upper body movement during human walking and running, in which the trunk and shoulders act primarily as elastic linkages between the pelvis, shoulder girdle and arms, the arms act as passive mass dampers which reduce torso and head rotation, and upper body movement is primarily powered by lower body movement. Supplementary material available online at Key words: arm swing, walking, running, passive dynamics, tuned mass dampers. INTRODUCTION Arm swing is a distinctive readily apparent characteristic of human walking and running. Our arms tend to swing out of phase with our legs, the right arm swinging forward with the left leg and vice versa. Although it has long been established that the arms do not swing as simple, unrestrained pendulums (Elftman, 939; Fernandez Ballesteros et al., 965; Jackson et al., 978; Hinrichs, 987; Ohsato, 993; Webb et al., 99; Gutnik et al., 25), the extent to which the shoulder muscles actively drive the arms, and the effect of arm swing on stability and economy during walking and running are poorly understood. In this paper, we examined the control of arm swing during walking and running, and investigated the effect of restricting arm swing on stability and metabolic cost. In a seminal study examining the movements of the torso and arms during walking, Elftman suggested that the arms did not move as simple pendulums, but instead were driven by muscle activation in the shoulder (Elftman, 939). Fernandez Ballesteros and colleagues expanded upon this work, using indwelling electrodes to measure muscle activity in the anterior, intermediate and posterior deltoid during walking, and confirmed that arm movement was accompanied by activity of the deltoid muscle, particularly during retraction (Fernandez Ballesteros et al., 965). Retraction of the shoulder was associated with firing of the posterior deltoid and, to a lesser extent, protraction of the shoulder was associated with anterior deltoid activity (Fernandez Ballesteros et al., 965). Further, Fernandez Ballesteros and colleagues showed that the shoulder muscles fire even when the arm is restrained during walking (Fernandez Ballesteros et al., 965), suggesting that the neural control of arm swing may be controlled by a locomotor pattern generator, and is perhaps an evolutionary hold-over from a quadrupedal past, a view supported by other workers (e.g. Gray, 9; Jackson et al., 978). Functionally, arm swing is often considered to be a mechanism for counteracting free vertical moments (i.e. torque about the body s vertical axis) imparted by the swinging legs. Elftman first proposed this mechanism for walking, showing that the angular acceleration of the arms was equal to that of the torso but in the opposing direction (Elftman, 939). Hinrichs provided similar evidence for running, showing that the horizontal angular momentum of the upper and lower body were of equal magnitude and in opposing directions, resulting in a net angular momentum near zero for the entire body (Hinrichs, 987; Hinrichs, 99). More recently, Herr and Popovic (Herr and Popovic, 28) showed that net angular momentum in all axes is kept remarkably close to zero during walking, and provided further evidence that arm moments serve to cancel lower limb moments about the body s vertical axis [figure 5C in Herr and Popovic (Herr and Popovic, 28)]. These results are consistent with those of Li and colleagues, which showed that the free vertical moments produced by the stance limb during walking are higher when the arms are restrained from swinging (Li et al., 2). Presumably, these greater vertical moments result from the absence of counteracting arm swing. It has also been suggested that restricting arm swing affects the metabolic cost of locomotion. Anderson and Pandy (Anderson and Pandy, 2), in comparing their forward dynamics simulation of human walking with experimental data from human subjects, suggested that the high cost
3 52 H. Pontzer and others of walking observed in their simulation resulted from the lack of arm swing in their model. Together with data on muscle activity (Fernandez Ballesteros et al., 965), these studies suggest that arm swing is largely driven by muscle activity in the shoulder, and serves an important role in maintaining stability during walking and especially during running. However, an alternative hypothesis is that arm swing is largely a passive response to the forces exerted on the torso by the swinging of the legs. According to this model, horizontal torques imparted on the pelvis by the swinging legs are transferred up the spinal column to the shoulder girdle, and then to the arms. Tonic or stabilizing muscle activity in the trunk and shoulder, along with ligamentous and other connective tissues, cause these elements to act as elastic elements or springs, an idea proposed by Fernandez Ballesteros and colleagues (Fernandez Ballesteros et al., 965); the forces exerted by these anatomical springs will increase in proportion to their angular displacement, or torsion. The direction of the torque transmitted through the trunk will alternate (clockwise/anti-clockwise) with each step as the legs swing in turn. The inertia of the torso and arms will tend to resist these forces, causing a time lag between movement in the pelvis and movement in the shoulder girdle. As a result, the shoulder girdle and arms will have the same oscillating frequency as the legs and pelvis, but will rotate out of phase with the legs. Viewing arm swing as a passive, emergent property of human walking and running fits well with recent work demonstrating the self-stabilizing, passive-dynamic nature of lower limb movement during walking (Collins et al., 25). In fact, even simple physical models can develop human-like arm swing in response to leg swing (see supplementary material Movie ). A passive model for arm swing would also have the advantage of being self-tuned, with greater leg accelerations leading to greater arm accelerations. Importantly, the effect of arm swing predicted by a passive model is similar to that suggested by active models, with the arms acting as mass dampers (see below), and angular acceleration of the upper body canceling horizontal angular accelerations by the swinging legs and maintaining whole-body net angular acceleration near zero. Lieberman and colleagues (Lieberman et al., 27; Lieberman et al., 28) have recently suggested that the arms act as mass dampers to minimize head pitch in the sagittal plane. Here, we examined the control and function of arm swing in human walking and running. First, we tested the hypothesis that the arms act as mass dampers that decrease the amplitude of upper body rotation about the vertical axis. We then investigated the control of arm swing, testing predictions of the passive arm swing hypothesis against those of an active arm swing hypothesis, in which arm swing is driven by the shoulder muscles. We measured muscle activity, kinematics and oxygen consumption during walking and running in a sample of humans. The moment of inertia of the arms was decreased by asking subjects to run with arms folded across their chest, or increased by adding weights at the elbow. We expected arm swing in humans to behave as a mass-damped system, with changes in the moment of inertia of the arms leading to predictable changes in upper body rotation. Further, we predicted that the arms would act as passive mass dampers, with the energy for arm swing ultimately derived from movement of the lower body, and the trunk and shoulders acting as damped spring elements. Finally, to examine the effect of normal arm swing in maintaining stability, we examined the effect of restraining the arms on locomotor kinematics, footfall variability and the energetic cost of walking and running. Modeling arms as mass dampers In mechanical systems exposed to vibration or other external forces, several approaches can be used to decrease the amplitude of displacement of the principle mass (see Soong and Dargush, 997). Systems for decreasing the amplitude of movement are generally termed energy dissipation systems, or dampers, and can be classed as passive or active. Passive dampers are those which impart no energy into the system, instead using the energy of the system to decrease movement of the principle mass (Symans and Constantinou, 999). For example, frictional dampers convert energy in the system to heat, reducing energy and movement in the principle mass (see supplementary material Movie ) (Soong and Dargush, 997). Tuned mass dampers (Soong and Dargush, 997) decrease movement of the principle mass by attaching an auxiliary mass using a damped spring (Fig. A). The effectiveness of passive tuned mass dampers is a complex function of the stiffness and damping constants of the damped spring by which they are attached but, generally, effectiveness is increased (i.e. movement of the principle mass is minimized) when the auxiliary mass is increased, and when the natural frequency of the auxiliary mass is below that of the principle mass (Soong and Dargush, 997). Active damping with auxiliary masses is also an effective strategy for minimizing displacement of a principle mass. Active mass damping differs from passive damping in that the auxiliary mass is attached with an active controller, so that the auxiliary mass can impart energy into the system, effectively pushing or pulling on the principle mass to stabilize it (Symans and Constantinou, 999). Notably, both active and passive mass dampers can be effective over a range of oscillation frequencies (Soong and Dargush, 997; Symans and Constantinou, 999). In the body, the torso is the principle mass whose angular displacement must be controlled. The hypothesis that the arms act as mass dampers for the torso thus leads to three predictions. First, since the effectiveness of mass dampers generally increases with their mass (Soong and Dargush, 997), decreasing the moment of inertia of the arms (the auxiliary mass) about the vertical (z) axis (Fig.2) as in the no arms condition is expected to result in greater rotation of the torso (the principle mass). Conversely, increasing the moment of inertia of the arms in the arm weights condition is expected to decrease torso rotation. A second, related prediction is that these changes in torso rotation should result in similar changes in head yaw, since the head is modeled as a mass attached to the torso via a damped spring (Fig.). Third, changes in the moment of inertia of the upper body (i.e. in the no arms or arm weights conditions) are predicted to have measurable effects on the phase differences in the movement of the pelvis and shoulder girdle. Increasing the moment of inertia of the arms, and therefore the upper body moment of inertia, is expected to lengthen the lag between pelvic and shoulder rotation, while decreasing the upper body moment of inertia is expected to shorten the lag between pelvic and shoulder movement. Passive arm swing model The passive arm swing hypothesis proposes that the upper body behaves like a passive mass-damped system (Soong and Dargush, 997; Symans and Constantinou, 999), in which all energy in the system derives from the swinging legs, and the spinal column and shoulders act as damped springs (Fig.B). This hypothesis leads to the following predictions. First, angular acceleration of the upper torso is predicted to increase with angular displacement between the pelvis and shoulder girdle (Fig.B). That is, as torsion of the spinal column increases, the force exerted by this spring-like
4 Arm swing in walking and running 525 A Controller Energy Mass Movement k c Mass 2 Position of mass Mass alone With mass 2 attached Time B Passive arm swing model C Active arm swing model Head Head Arms Arms x y Energy Torso Pelvis Torso Pelvis Energy Energy Legs Legs Fig.. Schematic diagram of passive and active arm swing hypotheses. (A) Simple mass damper (see Soong and Dargush, 997). Oscillating forces applied by a controller (red element) to the principle Mass will tend to move it (solid line in position plot); the attachment of an auxiliary Mass 2 using a damped spring can decrease the amplitude of movement of Mass (dashed line in position plot); the effectiveness of the damping is a function of the spring stiffness k and damping constant c, and is proportional to Mass 2. (B) In the passive arm swing model, oscillating moments from the swinging legs tend to accelerate the pelvis and other body segments in turn; all energy in the system is generated by the legs. The arms act as an auxiliary mass which damps movement of the torso (and head). Shoulder and arm accelerations are predicted to increase with angular displacement of the trunk (y) and shoulder (x), respectively. (C) In the active arm swing model, energy into the system comes from both the swinging legs and the shoulder muscles driving the arms. Accelerations of the pelvis and torso are expected to be negatively correlated (i.e. in opposition). Since forces of the shoulder muscles will accelerate both the arm and torso masses, albeit in opposing directions, arm acceleration is predicted to be negatively correlated with shoulder acceleration. In both passive and active models, oscillation of the torso and head will increase if arms are removed. Note that these systems (B and C) are rotational in nature, but are rendered as linear systems here for clarity. element will increase, resulting in greater acceleration of the shoulder girdle. Second, the angular acceleration of the arm is predicted to increase with angular displacement at the shoulder (i.e. the angle of the upper arm segment relative to vertical), just as the force generated by a spring increases with its displacement (Fig. B). In this way, rotation of the shoulders in the transverse plane is expected to result in arm swing in the sagittal plane. For example, as the shoulder girdle rotates and the right shoulder translates anteriorly, the arm will tend to remain in place following Newton s first law. Thus, the right arm will appear to swing posteriorly relative to the right shoulder, until the angular displacement of the shoulder is sufficient to swing the arm forward (protraction). As the right arm swings forward, the right shoulder will begin to translate posteriorly as the torso rotates with the next step, resulting again in angular displacement of the shoulder and acceleration of the arm. The shoulder musculature is expected to act as a spring-like element, translating angular displacement into torque. Thus a third prediction of the passive model is that the anterior and posterior portions of the deltoid will fire together, acting to stabilize the shoulder. Active arm swing model The active arm swing hypothesis proposes that arm swing is an active mass damping mechanism in which the arms (an auxiliary mass) are driven by the shoulder muscles acting as controllers in order to decrease the amplitude of torso rotation (Fig. B). Since the arm and torso are attached at the shoulder, anterior acceleration of the arm in the sagittal plane will lead to posterior acceleration of the shoulder and torso following Newton s third law: protraction of the right arm will tend to accelerate the right shoulder posteriorly, while retraction of the left arm will force the left shoulder anteriorly, thereby translating sagittal plane accelerations of the arms into
5 526 H. Pontzer and others transverse plane angular accelerations of the shoulders and torso. Thus the primary prediction of the active arm swing hypothesis is that increased anterior angular acceleration of the arm in the sagittal plane will result in increased posterior angular acceleration of the shoulder girdle in the transverse plane. Second, anterior and posterior deltoid fibers are expected to fire alternately, acting as agonists driving angular acceleration of the arm at the shoulder. Third, angular accelerations of the pelvis and shoulder girdle are predicted to be similar in magnitude but opposite in direction, as the upper body is driven to counteract vertical free moments produced by the swinging legs. Stability and cost To examine the function of arm swing in maintaining stability, we tested the effect of removing arm swing (no arms condition) on footfall variability and metabolic cost. If arm swing is critical for maintaining stability, then removing arm swing as in the no arms condition is expected create stability problems during walking and especially running, resulting in greater variability in footfall placement (Fig. B). Similarly, while the relationship between muscular work and metabolic cost is complex (Cavagna and Kaneko, 977; Willems et al., 995), if the muscular work is done to compensate for decreased stability in the no arms condition, the metabolic cost of locomotion in the no arms condition is expected to be greater relative to control walking and running (see Anderson and Pandy, 2). In contrast, if the upper body acts as a passive mass-damped system, then stability and cost should remain unchanged in the no arms condition, with the energy imparted by the swinging legs dissipated through greater excursion of the pelvis, torso and head. MATERIALS AND METHODS Sample Ten recreationally fit, healthy adult human subjects (six male, four female, mean ± s.d. body mass 6.9±.kg) with no apparent gait abnormalities participated in this study. Subjects gave their informed consent prior to participation. Washington University approval was obtained prior to the study, and institutional guidelines were followed throughout. Subjects wore spandex shorts, t-shirts or tank tops, and their personal running shoes throughout the experiment. Kinematics and muscle activity Small (cm diameter) spherical reflective markers were adhered to the body using double-sided tape, and the position of these markers was tracked using an infrared camera system (Vicon ; Centennial, CO, USA) recording at 2framess. Markers were placed on the following landmarks and locations: forehead (two markers), right and left acromia, right elbow, right wrist, right and left anterior superior iliac spines, right greater trochanter, right knee, right ankle (lateral malleolus), right and left heels, and right and left first toe (Fig. ). All markers were adhered directly to the skin, except those for the toe and heel, which were adhered to the subjects shoes. Anterior and posterior deltoid activity was recorded using selfadhering surface electrodes (Ambu Blue Sensor, Glen Burnie, MD, USA) and an electromyography (EMG) system (RunTech Myopac Jr, Mission Viejo, CA, USA). Subjects wore a light (32 g) amplifier unit that transmitted conditioned EMG signals along a fiber optic cable to a receiver. Analog signals were then passed through the Vicon MX Control A/D board and recorded at Hz in Vicon Nexus software, simultaneously with the kinematic data. Electrode placement was determined by palpation and confirmed by having the subject flex anterior and posterior portions of the deltoid individually against resistance while the EMG signal was observed. Although other muscles may also serve as shoulder flexors and extensors (e.g. triceps, biceps, latissimus dorsi), we focused on the deltoids here, since they have been shown to be important in this role during walking (Fernandez Ballesteros et al., 965). Additionally, other shoulder flexors serve multiple roles, such as elbow flexion and extension or arm rotation, making their action difficult to characterize. After being fitted with the EMG sensors and reflective markers, subjects performed an arm pump trial, in which they stood in place and swung their arms back and forth as during normal running. Next, after warming up on the treadmill (Sole Fitness F85, Jonesboro, AR, USA), subjects performed a series of walking and running treadmill trials for a range of speeds and experimental conditions. In the control condition, subjects walked normally at three speeds (.,.5 and 2.ms ) and ran normally at three speeds (2., 2.5 and 3.ms ). In the arm weight condition, these walking and running speeds were repeated, while the subject wore a.2 kg ankle-weight style weight on each arm, just proximal to the elbow. Finally, in the no arms condition, walking and running speeds were repeated again, with the subject instructed to keep their arms folded tightly across their chest. Note that the moment of inertia of the arms and upper body is increased in the arm weights condition, and decreased in the no arms condition, but the magnitude of change is likely to be different between conditions and among subjects. Data analysis Mean contact time (i.e. step duration), stride period and stride frequency were determined from five strides for each kinematic trial. Contact time was measured as the time between heel strike (the first kinematic frame showing heel ground contact) and toe-off (the last kinematic frame showing foot ground contact). Stride period was measured as the time between two consecutive right heel strikes. Marker position data were filtered in Matlab (MathWorks Inc., Natick, MA, USA) using a fourth-order, zero-lag Butterworth filter with a low-pass cut-off set at Hz. Filtered data were then used to calculate angle, angular velocity (deg.s ) and angular acceleration (deg.s 2 ) for different body segments. Angular displacements for the head, shoulder girdle and pelvis were calculated in the transverse plane using the two forehead markers, right and left acromia markers, and right and left anterior superior iliac spine markers, respectively (Fig.). For the right arm, the locations of the acromium, elbow and wrist markers were used to determine the location of the whole arm center of mass relative to the shoulder marker following Winter (Winter, 25). This point mass was then used to determine the angular displacement of the arm relative to the shoulder joint in the sagittal plane. EMG signals were band-pass filtered in Matlab using a fourthorder, zero-lag Butterworth filter with cut-offs at 6 and 3 Hz. Filtered signals were then processed using Thexton s randomization method (Thexton, 996). The signal was recitified and binned following Winter (Winter, 25) using a. s reset integral. Thextonization requires a threshold, set at % of the maximum integrated signal. The number of times the signal rose above this threshold ( runs ) was determined for each 8 s trial. The threshold was then raised by.5% of the maximum integrated signal and the number of runs was found. This process was repeated, each time raising the threshold by.5% of the maximum integrated signal, until the threshold was equal to the maximum magnitude. The signal was then randomized, and the threshold method was repeated on the randomized signal. The number of runs in the randomized signal was subtracted from the number of runs in the original signal, and
6 Arm swing in walking and running 527 Arm rotation (+) * α ( ) Head rotation (+) (yaw) Shoulder rotation (+) Pelvis rotation (+) et al., 98); the system was calibrated daily and checked for leaks using a known flow rate of pure nitrogen. The resting rate of oxygen consumption was first measured with the subjects standing on the treadmill. Next, the subjects performed two.5ms walking trials, and two 3.ms running trials. In one walking trial and one running trial the subjects walked or ran normally, as in the control condition; in the other walking and running trial, they walked or ran with arms folded tightly across their chest as in the no arms condition. The order of conditions was varied, so that half of the subjects performed the control trials first, and half performed the no arms condition first. Each metabolic trial lasted at least 6min, and mean oxygen concentration from the final 2 min of each trial was used to calculate the rate of oxygen consumption. Only trials in which oxygen consumption visibly reached a plateau (less than % change over the final 2min) were used for analysis. For each subject, the resting rate of oxygen consumption was subtracted from the rate of consumption while walking or running in order to calculate a net cost of locomotion. This net cost was then divided by body mass and then by speed to give the mass-specific cost of transport (ml O 2 kg m ) for each speed in each condition. y Step width x z Fig. 2. Schematic diagram of the reference frame and kinematic variables. Rotation of the head, shoulders and pelvis in the transverse (x y) plane about the vertical (z) axis was measured using reflective markers (gray circles) with reference to the x-axis; arrows indicate positive rotation. Trunk torsion was measured as the rotation of the pelvis relative to the shoulders. Arm rotation was measured in the sagittal (y z) plane using the reconstructed arm center of mass (*) and shoulder relative to vertical; arrow indicates positive rotation. Angular displacement of the shoulder (α) was defined as negative when the arm was retracted (as shown), positive when protracted. Step width was measured as the difference in x-position of successive heel strikes. the maximum difference was set as the threshold for the lowest muscle activity. All values below this threshold (e.g. values lower than random muscle activity) were removed from the original signal. Metabolic cost of locomotion After the kinematic trials described above, a subset (N=6, four male, two female, 7.2±5.9kg) of subjects performed a set of metabolic trials in order to determine the effect of arm restraint on locomotor cost. For these trials, oxygen consumption was measured using the open-flow method described previously (Fedak et al., 98; Pontzer, 27). Subjects wore a light mask through which air was pulled at 25 l min. This air was sub-sampled continuously, scrubbed of water vapor and carbon dioxide, and analyzed for oxygen concentration using a paramagnetic analyzer (Sable Systems, Las Vegas, NV, USA). Oxygen concentration was monitored in near-real time and recorded at 3Hz in Vicon Nexus software. Oxygen concentration was then used to calculate the rate of oxygen consumption (ml O 2 s ) following Fedak et al. (Fedak Hypothesis testing Filtered kinematic and thextonized EMG data were used to examine predicted relationships. Segment velocities and accelerations were calculated using the finite differences method described in Winter (Winter, 25). Predictions were considered to be supported if the correlation between two kinematic variables (e.g. shoulder displacement and arm acceleration) had a Pearson s R greater than.5 or less than.5, and in the predicted direction, following Cohen s index for a large effect size (Cohen, 992). This effect size (R=±.5) recognizes the complexity of the multi-segment, multimuscle system being analyzed, and anticipates variability within the system and between subjects. It should be noted that the conventional criterion for statistical significance, a P-value of <.5 or <., is inappropriate in determining the biological or biomechanical significance of these segment correlations due to the large number of data points generated by high-speed kinematic data. With a capture rate of 2 frames s, three strides generate approximately 6 data points, because each frame produces a position, velocity and acceleration estimate for a given segment. With a sample of 6 points, even small correlations of R=±. become significant at P<.; however, such small correlations indicate that only % of the variance in the dependent variable is explained by the independent variable. Therefore the criterion for a large effect size (R=±.5) (Cohen, 992), while admittedly arbitrary, is preferable to a calculated P-value for these correlations. To determine the effect of the no arms condition on locomotor cost, we compared the net mass-specific cost of locomotion in the control and no arms condition during walking and running for each subject using Student s one-tailed, paired t-test. Similarly, we used Student s one-tailed, paired t-test to compare mean contact times, stride frequencies, head yaw amplitude and footfall variability for each subject walking at.5ms and running at 3.ms in each condition. Note that using a one-tailed test was deemed appropriate here, since the direction of the predicted difference is known a priori. We discuss the effect of using a one-tailed test below. Lag time between shoulder and pelvis rotation and footfall variability were also compared between conditions using Student s paired t-tests. As pelvis and shoulder rotation occur with similar frequency but with different times of peak amplitude, we calculated the phase difference between pelvis and shoulder movement in order
7 528 H. Pontzer and others to determine the effect of increasing or decreasing the moment of inertia of the upper body. The phase difference between peak pelvis rotation (t pelvis ) and peak shoulder rotation (t shoulder ) was calculated as phase difference=36deg. ( t pelvis t shoulder /stride period). The closest shoulder and pelvis peaks were compared, so that the maximum phase difference was 8 deg. To test for differences in footfall variability, the medio-lateral position of the heel at heel strike was recorded for eight consecutive steps at each speed (Fig. ). The medio-lateral distance between successive steps, hereafter termed step width, was measured, and the coefficient of variation (a sizecorrected measure of variance) was determined for each subject at each speed. Coefficients of variation (c.v.) were then compared using Student s paired t-test. Shoulder rotation amplitude (deg.) A B Arm weights Control No arms RESULTS Kinematics Kinematic analyses revealed correlated movements of the pelvis, shoulder and arm which support the hypothesis that the arms act as mass dampers, decreasing the amplitude of upper body rotation. Changing the moment of inertia of the arms (and hence the upper body) generally resulted in the predicted effects on the amplitude of upper body rotation (measured as shoulder rotation; Fig. 3A) and of the head (measured as the amplitude of head yaw; Fig.3B), although this effect was stronger during running. For walking trials at.5ms, shoulder rotation was generally low, and there were no significant differences between no arms (mean±s.d. 8.6±.9 deg.) and control (8.±2.5 deg.) conditions (P=.2), or between control and arm weights (9.±3. deg.) conditions (P=.33; Fig. 3A). In contrast, during running at 3.ms, the amplitude of shoulder rotation was significantly greater (P<.) and changes in arm inertia had expected effects on shoulder rotation. Decreasing the moment of inertia of the arms in the no arms condition resulted in greater shoulder rotation (35.68 deg.) than in control trials (23.75 deg., P<.; Fig. 3A), while increasing the moment of inertia of the arms in the arm weights condition resulted in decreased shoulder rotation (7.8 deg.) compared with control trials, although this relationship barely met the significance criterion (P=.9). The amplitude of head rotation was significantly lower than that of the shoulder in all conditions, both walking and running (P<. all comparisons; Fig. 3B). Still, changes in head yaw between conditions generally followed the pattern of shoulder rotation. During walking, head yaw was lowest in arm weights trials (5.±.7 deg.), slightly greater in control trials (5.2±. deg.) and greatest in no arms trials (6.±.6 deg.). Significant differences were found between no arms and control trials (P=.6), and between no arms and arm weights trials (P=.), but differences between control trials and arm weights (P=.32) and no arms trials were not significant. During running, head yaw was lowest in arm weights trials (5.3±.5 deg.), slightly greater in control trials (6.±.6 deg.) and greatest in no arms trials (.3±3. deg.). The difference between no arms and both arm weights (P<.) and control trials (P<.) was significant, but the difference between control and arm weights conditions (P=.26) was not. For all conditions, head yaw tended to be greater during running than during walking, but this difference was only significant for the no arms condition (P<.). Lag time between pelvis and shoulder rotation increased with greater moment of inertia of the upper body as predicted (Fig.3C), with the greatest phase differences between pelvis and shoulder rotation during arm weights trials for both walking (57.6±22.deg.) and running (7.±35.8deg.). Phase differences in control trials were slightly lower (walking 9.2±.5deg., running 93.9±6.9deg.) but Head yaw amplitude (deg.) Phase difference (deg.) Pelvis versus shoulder rotation C Walking Running Fig. 3. Mean ± s.d. (A) shoulder rotation, (B) head yaw and (C) phase differences between peak shoulder rotation and peak pelvis rotation. *Significant difference compared with control trials (P<.5). Significant difference compared with arm weights trials (P<.5). Significant difference compared with both arm weights and control trials (P<.5). * these differences were not significant (walking P=., running P=.6). Phase differences were smallest in the no arms trials (walking 93.9±6.9 deg., running 33.±23.3 deg.), significantly smaller than control trials for both gaits (walking P=., running P<.), and significantly smaller than arm weights trials during running (running P<., walking comparison approach significance at P=.55). For each condition, phase differences were significantly greater during walking (P<., walking versus running trials, all comparisons). Passive arm swing predictions were strongly supported by kinematic results. During walking and running, angular acceleration of the shoulders in the transverse plane was consistently, positively correlated with torsion of the spinal column, measured as the difference in angle between the shoulder and pelvis in the transverse plane (mean Pearson s R=.59; Table ; Fig. ). Similarly, for both walking and running trials, angular acceleration of the arm in the sagittal plane was strongly correlated with angular displacement of the shoulder, with greater retraction associated with greater anterior
8 Arm swing in walking and running 529 Table. Correlations (Pearson s R) between body segments during normal walking and running Passive arm swing Active arm swing Pelvis shoulder angle versus shoulder acceleration Speed/gait Mean s.d.. m s walk.5.3 (.387,.736).5 m s walk..5 (.2,.667) 2. m s walk..97 (.7,.7) 2. m s run (.266,.82) 2.5 m s run.75. (.562,.887) 3. m s run.75.8 (.589,.835) Walking.5.6 (.7,.736) Running.7.33 (.266,.98) All (.7,.98) Arm angle versus arm acceleration (Min., max.) Mean s.d (.889,.57) (.955,.672) (.952,.758).8.8 (.889,.773).8.5 (.895,.776).85.8 (.93,.778).83.2 (.955,.57).8. (.93,.773).8.85 (.955,.57) (Min., max.) Mean s.d. Pelvis acceleration versus shoulder acceleration..9 (.8,.266).5.92 (.,.8) (.7,.29) (.385,.22)..259 (.365,.33) (.3,.33)..5 (.7,.266)..238 (.3,.33)..97 (.3,.33) Arm acceleration versus shoulder acceleration (Min., max.) Mean s.d (Min., max.) (.229,.365) (.286,.72) (.55,.667) (.8,.58) (.9,.598) (.22,.65) (.286,.667) (.8,.7) (.286,.7) acceleration (mean Pearson s R=.59; Table ; Fig. ). These results are consistent with the passive arm swing prediction that the spinal column and shoulder effectively act as springs, with greater displacement leading to greater acceleration. Active arm swing predictions were generally not supported by kinematic analyses. Angular accelerations of the pelvis and shoulder were not correlated (mean Pearson s R=.; Table ; Fig. ). Further, while arm acceleration was weakly correlated with the angular acceleration of the shoulder (mean Pearson s R=.27; Table ; Fig. ), the positive direction of correlation was opposite to that of the active arm swing hypothesis, which predicts that anterior acceleration of the arm will lead to posterior acceleration of the ipsilateral shoulder. Comparing walking and running (Table ), it is evident that Pearson s correlations between shoulder acceleration and both arm acceleration and spinal torsion are greater during running. The significance of this change and the underlying mechanism are unclear. In both cases, the greater ground forces encountered during running may lead to greater stabilizing muscle activity, and therefore a stronger linkage (i.e. a stiffer spring ) between the pelvis, shoulder and arm. Stiffer springs may also be necessitated by the greater stride frequencies used in running, since stiffer springs would increase the natural frequencies for the body segments involved. For example, a stiffer spring in the shoulder will increase the natural frequency of the swinging arm. Finally, the greater angular excursions seen in running (Fig. 3A,B) may lead to a stronger correlation of movement between segments. Muscle activity Patterns of muscle firing were generally consistent with predictions of the passive arm swing hypothesis, although some alternating activity in the anterior and posterior deltoid was observed. When compared with the clear alternating pattern of anterior and posterior deltoid activity seen in the arm pump trials (Fig.5A), firing of these muscles during both walking and running was largely simultaneous. This suggests that the deltoid is acting to stabilize the shoulder as predicted by the passive arm swing hypothesis, rather than to drive it anteriorly or posteriorly as predicted by the active arm swing hypothesis. However, some alternating activity was observed, particularly in walking trials (Fig. 5B), indicating that the deltoid does drive arm swing at least occasionally for some individuals. During running, firing of the anterior and posterior portions of the deltoid was almost exclusively co-contraction (Fig. 5C). Overlaying the angular velocity and acceleration of the shoulder in the sagittal plane on EMG activity (Fig.6), it appears that many, perhaps most, of the deltoid contractions are eccentric, with the anterior deltoid firing while the arm moves posteriorly, and the posterior deltoid firing while the arm moves anteriorly. These eccentric contractions are consistent with the view of the shoulders as spring-like linkages. Further, while contraction of the anterior or posterior deltoid is typically associated with predictable accelerations at the shoulder, there are also periods in which arm acceleration and deltoid activity are in opposition, with anterior acceleration of the arm associated with posterior deltoid activity (Fig. 6A), even when the lag time between activation and force production are considered. Similarly, periods of arm acceleration are also seen when the deltoid muscles are quiet (Fig. 6B). These patterns suggest that forces, in addition to those from the deltoid, are acting on the arm. These results are consistent with the mass damping hypothesis, in which forces acting on the arms are primarily derived from the legs via the trunk. Gait characteristics Stride period during no arms trials (walking.5±.6 s, running.7±. s) was similar to that in control (walking.5±.7 s, running.75±. s) and arm weights trials (walking.±.5 s, running.76±.8 s). These differences were not significant for walking or running (P>.5) with the exception of the control no arms comparison for running (P<.). However, this difference was small (. s, or.3%) and probably biomechanically unimportant. Contact times during no arms trials (walking.68±.5s, running.3±.3s), control trials (walking.68±.5s, running.3±.3 s) and arm weights trials (walking.68±.5 s, running.32±.3 s) were similar (P>.5 all comparisons).
9 53 H. Pontzer and others A Shoulder angular acceleration (deg. s 2 ) Sub. 3. m s Walking Running Trunk torsion (deg.) 2 Sub m s B C 3 5 D 3 Arm angular acceleration (deg. s 2 ) E Shoulder angular acceleration (deg. s 2 ) Sub. 2 Sub. 2. m s 3. m s 5 Sub. 9.5 m s Shoulder displacement (deg.) Pelvis angular acceleration (deg. s 2 ) Sub m s F Count (trials) G Shoulder angular acceleration (deg. s 2 ) Sub..5 m s Sub m s H 5 6 Arm angular acceleration (deg. s 2 ) Pearson s R Fig.. Kinematic results. (A D) Predictions of the passive arm swing hypothesis (see Fig. 2B); (E H) active arm swing predictions (see Fig. 2C). Plots are representative results for walking and running and list the subject (Sub.) and speed shown. Histograms are Pearsonʼs R-values for all speeds and subjects, walking and running combined. Hatched areas in histograms indicate predicted values for passive (B,D) or active (F,H) hypotheses. Footfall variation and metabolic cost During walking at.5ms, variation in step width during no arms trials (mean c.v..53±.26) was greater than for control trials (.±.2) although this difference was only marginally significant (P=.39). There was no difference between control and arm weights (.56±.3) conditions, or between no arms and arm
10 Arm swing in walking and running 53 A Arm pump Anterior deltoid Posterior deltoid 2 2 scaled Adelt Sub. 2 Sub. 3 scaled Pdelt B Walking,.5 m s Normalized muscle activity Sub. 2 scaled Adelt scaled Pdelt 2 Sub. 7 scaled Adelt scaled Pdelt C Running, 3. m s 2 2 scaled Adelt Sub. 8 Sub. scaled Pdelt Time (s) Fig. 5. Representative anterior and posterior deltoid activity for (A) arm pump, (B).5 m s walking, and (C) 3. m s running trials. EMG data have been processed as described in the text and normalized to the maximum activation within a trial. The subject from whom data were obtained is listed. weights conditions (P>. both comparisons; Fig. 7A). During running at 3.ms, there were no differences between no arms (.59±.2), control (.53±.8) and arm weights trials (.8±.7; Fig. 7A). Restricting arm swing in the no arms condition had no effect on the mass-specific energetic cost of transport (ml O 2 kg m ). Locomotor costs during no arms trials (walking.3±.3 ml O 2 kg m, running.2±.ml O 2 kg m ) and control trials (walking.2±.2ml O 2 kg m, running.2±.ml O 2 kg m ) were similar (walking P=., running P=.; Fig. 7B). DISCUSSION Arms as mass dampers Our results support the hypothesis that the arms act as mass dampers during human walking and running, although the evidence is clearest for running. In running trials, the amplitude of shoulder
11 532 H. Pontzer and others Normalized EMG Normalized EMG A Posterior deltoid Anterior deltoid.5 m s walk Subject B 3. m s run Subject Posterior deltoid Anterior deltoid Angular velocity (deg. s ) 3 Angular velocity (deg. s ) 3 Angular acceleration (deg. s 2 ) Angular acceleration (deg. s 2 ) 3 3 Fig. 6. Representative angular velocity (red line) and angular acceleration (blue line) for the arm at the shoulder, overlaid on normalized anterior and posterior deltoid activity, during (A) walking at.5 m s and (B) running at 3. m s. Deltoid activity is processed and shown as in Fig. 5. Periods of apparent eccentric contraction are indicated (red arrows), as are periods in which shoulder acceleration is in opposition to prevailing muscle activity (blue arrows) or occurs without substantial deltoid activity (black arrows). Not all such periods are indicated. rotation clearly increased when the moment of inertia of arms decreased (Fig. 3A), just as movement the principle mass of a massdamped system should increase with a decrease in the auxiliary mass (Fig. A) (Soong and Dargush, 997). While this relationship was not observed for walking (Fig.A), this does not mean that a massdamper view of the arms should be rejected; the effectiveness of a mass damper and the effect of changing its inertial properties depend upon the magnitude and frequency of the external forces acting on the system (Soong and Dargush, 997). The magnitude and frequency of forces from the lower body may simply be too low during walking to elicit a significant change in torso movement with the manipulations of arm inertial properties used here. The magnitude of head yaw was less than that of the shoulders, but changes in head yaw across experimental conditions generally followed the pattern of shoulder movement, supporting the view of the head as a mass attached via a damped spring. Finally, phase lag between the lower body and upper body decreased when the moment of inertia of the arms was decreased during both walking and running (Fig.C), as predicted for a mass-damped system. The view of the arms as mass dampers is consistent with previous work (e.g. Hinrichs, 987; Hinrichs, 99; Li et al., 2; Herr and Popovic, 28) indicating that angular acceleration in the upper and lower body tend to cancel, resulting in near-zero net moments about the vertical axis. However, while the results of this study fit predictions of a mass-damper model, the tests here are certainly not exhaustive, and future work might test other predictions of a mass-damper hypothesis in order to determine whether this model alone is sufficient for explaining upper body movement, particularly during walking. Passive versus active arm swing The passive arm swing hypothesis proposes that upper body movement is driven by movement in the legs and pelvis, with force transferred to the shoulders and arms via spring-like elements (ligaments and muscles) in the spine and shoulder. This differs from an active arm swing hypothesis, which proposes that upper body movement is driven primarily by swinging the arms using the shoulder muscles. As predicted by the passive arm swing hypothesis, angular acceleration of the shoulders was correlated with increased trunk torsion, and arm acceleration was strongly correlated with angular displacement of the shoulder (Fig. ). In contrast, angular acceleration of the shoulders and pelvis were not inversely correlated, nor was shoulder acceleration inversely correlated with arm acceleration, as predicted by the active arm swing hypothesis (Fig. ). EMG recordings of the anterior and posterior deltoid suggest that, while these muscles may play a limited role in driving arm swing, they act primarily to stabilize the shoulder through cocontraction or eccentric contractions (Figs 5 and 6). Taken together, the kinematic and EMG results support the passive arm swing hypothesis. Additional support for the passive arm swing model comes from the metabolic comparisons of control and no arms conditions. As noted above, upper body movement during running increases in the no arms condition by approximately 5% compared with control trials (Fig. A). If upper body movement is actively driven by trunk and arm musculature as in the active arm swing model, the larger displacements of the torso should require a corresponding increase in oxygen consumption. Instead, energy use is similar to that in the control condition, indicating that greater movement of the torso in
12 Arm swing in walking and running 533 Step width variation (c.v.) Cost of transport (ml O 2 kg m ) A B Arm weights Control No arms * Control No arms Walking Running Fig. 7. Mean ± s.d. values for walking (.5 m s ) and running (3. m s ) for (A) step width variation and (B) locomotor cost. *Significant difference compared with control trials (P<.5). the no arms trials results from the decreased inertia of the upper body, not an increase in muscle activity. Further tests of the passive mass damping model While our results support the hypothesis that the upper body behaves as a passive system, limitations in our methods must be considered. Perhaps most critically, our analysis of muscle activity is limited to surface EMG of the deltoids, and further data are needed to determine whether muscles and other connective tissues in the back and shoulder performed mechanical work or acted as springs. Our analyses suggest these linkages behave like springs, but the possibility that muscles are performing work while mimicking purely elastic behavior cannot be ruled out using our methods; such pseudo-elastic muscle activity has been suggested before for the leg muscles during terrestrial locomotion (Ruina et al., 25). Even if the muscular linkages involved do act as springs, without performing positive mechanical work, it is important to note that such isometric or eccentric muscle contraction incurs a metabolic cost. Thus, arm swing may be passive in the mechanical sense, with energy for movement being derived ultimately from leg swing, and yet be active in the metabolic sense, requiring metabolic energy for muscle activation. It is also important to note that mass-damped systems can respond in complex ways to changes in the oscillation frequency, spring and damping constants, and relative masses of the segments (Soong and Dargush, 997). Our simple five-segment model essentially treats these variables as constant across conditions, but this assumption is difficult to test and not addressed here. More sophisticated models, in concert with more in-depth measurements of muscle activity, may provide a more comprehensive test of the mass damping model for upper body mechanics. Specifically, expanding current forward dynamics models of human walking (e.g. Anderson and Pandy, 2) to include full musculoskeletal treatment of the trunk and arms will provide a means of examining the interaction between upper and lower body movement. Both the active arm swing and passive arm swing hypotheses predict that net moments about the body s vertical axis will be kept near zero for steady-state walking and running, and thus net-moment analyses are not able to distinguish between these two mechanisms. Our passive arm swing hypothesis differs primarily in that the power for arm swing is ultimately derived from the swing legs. As such, future work might examine non-steady-state locomotion in which lower limb energy changes, such as with the increase in stride frequency associated with increased walking speed. Active arm swing models would predict these changes to be immediately matched by corresponding changes in upper body movement, whereas a passive model would predict a measurable lag time of at least one step (i.e. one oscillation of the pelvis in the transverse plane) for the increased energy in the legs to be transferred to the upper body. By highlighting the importance of spring-like mechanisms in the trunk and shoulder, our work builds upon that of Fernandez Ballesteros and colleagues (Fernandez Ballesteros et al., 965), which suggested that elastic mechanisms in the shoulder are critical to normal arm swing. This view of arm swing as an emergent property of human walking also fits well with recent passivedynamic models of lower limb mechanics for human walking (Collins et al., 25). As with passive-dynamic lower limb movement, passive spring-driven arm swing mechanics proposed here are inherently self-tuning without requiring extensive feedforward neurological control. Passive-dynamic walkers which include upper body segments connected to the lower body through elastic elements would provide a further test of the passive arm swing hypothesis, and perhaps refine current models for upper body movement in humans. The role of arm swing in walking and running With the exception of a small, mechanically negligible decrease in stride frequency during no arms running and a small but statistically significant increase in footfall variability during no arms walking, restricting arm swing or adding weights to the arms had no effect on the lower limb kinematics or footfall variability measured here, nor did restricting arm swing affect walking or running cost (Fig. 7B). These results provide further support for the idea that upper body movement is inherently self-tuned, producing stable walking and running even when upper body inertial properties are modified. However, as a consequence of this self-tuning, upper body kinematics were significantly affected by restricting arm swing, with shoulder rotation and head yaw increasing substantially in no arms running trials (Fig. 3A,B). These results, as well as the relative isolation of the head from the larger rotations experienced by the shoulders, support Bramble and Lieberman s (Bramble and Lieberman, 2) hypothesis that the derived configuration of the human upper body in which humans have low, wide shoulders that are mostly decoupled from the head are exaptive for walking, and are especially important for limiting head yaw and improving visual stability during running. The importance of normal arm swing in reducing head yaw in humans raises the question of how cursorially adapted birds
GROUND REACTION FORCE DOMINANT VERSUS NON-DOMINANT SINGLE LEG STEP OFF
 GROUND REACTION FORCE DOMINANT VERSUS NON-DOMINANT SINGLE LEG STEP OFF Sara Gharabaghli, Rebecca Krogstad, Sara Lynch, Sofia Saavedra, and Tamara Wright California State University, San Marcos, San Marcos,
GROUND REACTION FORCE DOMINANT VERSUS NON-DOMINANT SINGLE LEG STEP OFF Sara Gharabaghli, Rebecca Krogstad, Sara Lynch, Sofia Saavedra, and Tamara Wright California State University, San Marcos, San Marcos,
-Elastic strain energy (duty factor decreases at higher speeds). Higher forces act on feet. More tendon stretch. More energy stored in tendon.
 As velocity increases ( ) (i.e. increasing Froude number v 2 / gl) the component of the energy cost of transport associated with: -Internal kinetic energy (limbs accelerated to higher angular velocity).
As velocity increases ( ) (i.e. increasing Froude number v 2 / gl) the component of the energy cost of transport associated with: -Internal kinetic energy (limbs accelerated to higher angular velocity).
(2) BIOMECHANICS of TERRESTRIAL LOCOMOTION
 (2) BIOMECHANICS of TERRESTRIAL LOCOMOTION Questions: - How does size influence the mode and speed of locomotion? - What determines the energy cost of locomotion? - Why do humans walk and run the way we
(2) BIOMECHANICS of TERRESTRIAL LOCOMOTION Questions: - How does size influence the mode and speed of locomotion? - What determines the energy cost of locomotion? - Why do humans walk and run the way we
Assessments SIMPLY GAIT. Posture and Gait. Observing Posture and Gait. Postural Assessment. Postural Assessment 6/28/2016
 Assessments 2 SIMPLY GAIT Understanding movement Evaluations of factors that help therapist form professional judgments Include health, palpatory, range of motion, postural, and gait assessments Assessments
Assessments 2 SIMPLY GAIT Understanding movement Evaluations of factors that help therapist form professional judgments Include health, palpatory, range of motion, postural, and gait assessments Assessments
The Starting Point. Prosthetic Alignment in the Transtibial Amputee. Outline. COM Motion in the Coronal Plane
 Prosthetic Alignment in the Transtibial Amputee The Starting Point David C. Morgenroth, MD, Department of Rehabilitation Medicine University of Washington VAPSHCS Outline COM Motion in the Coronal Plane
Prosthetic Alignment in the Transtibial Amputee The Starting Point David C. Morgenroth, MD, Department of Rehabilitation Medicine University of Washington VAPSHCS Outline COM Motion in the Coronal Plane
RUNNING SHOE STIFFNESS: THE EFFECT ON WALKING GAIT
 RUNNING SHOE STIFFNESS: THE EFFECT ON WALKING GAIT Stephen N Stanley, Peter J M c Nair, Angela G Walker, & Robert N Marshall Auckland Institute of Technology, Auckland, New Zealand University of Auckland,
RUNNING SHOE STIFFNESS: THE EFFECT ON WALKING GAIT Stephen N Stanley, Peter J M c Nair, Angela G Walker, & Robert N Marshall Auckland Institute of Technology, Auckland, New Zealand University of Auckland,
Normal and Abnormal Gait
 Normal and Abnormal Gait Adrielle Fry, MD EvergreenHealth, Division of Sport and Spine University of Washington Board Review Course March 6, 2017 What are we going to cover? Definitions and key concepts
Normal and Abnormal Gait Adrielle Fry, MD EvergreenHealth, Division of Sport and Spine University of Washington Board Review Course March 6, 2017 What are we going to cover? Definitions and key concepts
+ t1 t2 moment-time curves
 Part 6 - Angular Kinematics / Angular Impulse 1. While jumping over a hurdle, an athlete s hip angle was measured to be 2.41 radians. Within 0.15 seconds, the hurdler s hip angle changed to be 3.29 radians.
Part 6 - Angular Kinematics / Angular Impulse 1. While jumping over a hurdle, an athlete s hip angle was measured to be 2.41 radians. Within 0.15 seconds, the hurdler s hip angle changed to be 3.29 radians.
Transformation of nonfunctional spinal circuits into functional states after the loss of brain input
 Transformation of nonfunctional spinal circuits into functional states after the loss of brain input G. Courtine, Y. P. Gerasimenko, R. van den Brand, A. Yew, P. Musienko, H. Zhong, B. Song, Y. Ao, R.
Transformation of nonfunctional spinal circuits into functional states after the loss of brain input G. Courtine, Y. P. Gerasimenko, R. van den Brand, A. Yew, P. Musienko, H. Zhong, B. Song, Y. Ao, R.
Biomechanics and Models of Locomotion
 Physics-Based Models for People Tracking: Biomechanics and Models of Locomotion Marcus Brubaker 1 Leonid Sigal 1,2 David J Fleet 1 1 University of Toronto 2 Disney Research, Pittsburgh Biomechanics Biomechanics
Physics-Based Models for People Tracking: Biomechanics and Models of Locomotion Marcus Brubaker 1 Leonid Sigal 1,2 David J Fleet 1 1 University of Toronto 2 Disney Research, Pittsburgh Biomechanics Biomechanics
Current issues regarding induced acceleration analysis of walking using the integration method to decompose the GRF
 Current issues regarding induced acceleration analysis of walking using the integration method to decompose the GRF George Chen May 17, 2002 Stanford Neuromuscular Biomechanics Lab Group Muscle contribution
Current issues regarding induced acceleration analysis of walking using the integration method to decompose the GRF George Chen May 17, 2002 Stanford Neuromuscular Biomechanics Lab Group Muscle contribution
An investigation of kinematic and kinetic variables for the description of prosthetic gait using the ENOCH system
 An investigation of kinematic and kinetic variables for the description of prosthetic gait using the ENOCH system K. OBERG and H. LANSHAMMAR* Amputee Training and Research Unit, University Hospital, Fack,
An investigation of kinematic and kinetic variables for the description of prosthetic gait using the ENOCH system K. OBERG and H. LANSHAMMAR* Amputee Training and Research Unit, University Hospital, Fack,
Toward a Human-like Biped Robot with Compliant Legs
 Book Title Book Editors IOS Press, 2003 1 Toward a Human-like Biped Robot with Compliant Legs Fumiya Iida a,b,1, Yohei Minekawa a Juergen Rummel a and Andre Seyfarth a a Locomotion Laboratory, University
Book Title Book Editors IOS Press, 2003 1 Toward a Human-like Biped Robot with Compliant Legs Fumiya Iida a,b,1, Yohei Minekawa a Juergen Rummel a and Andre Seyfarth a a Locomotion Laboratory, University
CHAPTER IV FINITE ELEMENT ANALYSIS OF THE KNEE JOINT WITHOUT A MEDICAL IMPLANT
 39 CHAPTER IV FINITE ELEMENT ANALYSIS OF THE KNEE JOINT WITHOUT A MEDICAL IMPLANT 4.1 Modeling in Biomechanics The human body, apart of all its other functions is a mechanical mechanism and a structure,
39 CHAPTER IV FINITE ELEMENT ANALYSIS OF THE KNEE JOINT WITHOUT A MEDICAL IMPLANT 4.1 Modeling in Biomechanics The human body, apart of all its other functions is a mechanical mechanism and a structure,
Body Stabilization of PDW toward Humanoid Walking
 Body Stabilization of PDW toward Humanoid Walking Masaki Haruna, Masaki Ogino, Koh Hosoda, Minoru Asada Dept. of Adaptive Machine Systems, Osaka University, Suita, Osaka, 565-0871, Japan ABSTRACT Passive
Body Stabilization of PDW toward Humanoid Walking Masaki Haruna, Masaki Ogino, Koh Hosoda, Minoru Asada Dept. of Adaptive Machine Systems, Osaka University, Suita, Osaka, 565-0871, Japan ABSTRACT Passive
BIOMECHANICAL MOVEMENT
 SECTION PART 5 5 CHAPTER 12 13 CHAPTER 12: Biomechanical movement Practice questions - text book pages 169-172 1) For which of the following is the athlete s centre of mass most likely to lie outside of
SECTION PART 5 5 CHAPTER 12 13 CHAPTER 12: Biomechanical movement Practice questions - text book pages 169-172 1) For which of the following is the athlete s centre of mass most likely to lie outside of
Increasing ankle push-off work with a powered prosthesis does not necessarily reduce metabolic rate for transtibial amputees
 Supplementary Materials Increasing ankle push-off work with a powered prosthesis does not necessarily reduce metabolic rate for transtibial amputees Roberto E. Quesada, Joshua M. Caputo,, and Steven H.
Supplementary Materials Increasing ankle push-off work with a powered prosthesis does not necessarily reduce metabolic rate for transtibial amputees Roberto E. Quesada, Joshua M. Caputo,, and Steven H.
video Purpose Pathological Gait Objectives: Primary, Secondary and Compensatory Gait Deviations in CP AACPDM IC #3 1
 s in CP Disclosure Information AACPDM 71st Annual Meeting September 13-16, 2017 Speaker Names: Sylvia Ounpuu, MSc and Kristan Pierz, MD Differentiating Between, Secondary and Compensatory Mechanisms in
s in CP Disclosure Information AACPDM 71st Annual Meeting September 13-16, 2017 Speaker Names: Sylvia Ounpuu, MSc and Kristan Pierz, MD Differentiating Between, Secondary and Compensatory Mechanisms in
Gait. Kinesiology RHS 341 Lecture 12 Dr. Einas Al-Eisa
 Gait Kinesiology RHS 341 Lecture 12 Dr. Einas Al-Eisa Definitions Locomotion = the act of moving from one place to the other Gait = the manner of walking Definitions Walking = a smooth, highly coordinated,
Gait Kinesiology RHS 341 Lecture 12 Dr. Einas Al-Eisa Definitions Locomotion = the act of moving from one place to the other Gait = the manner of walking Definitions Walking = a smooth, highly coordinated,
Supplementary Figure S1
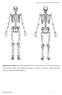 Supplementary Figure S1: Anterior and posterior views of the marker set used in the running gait trials. Forty-six markers were attached to the subject (15 markers on each leg, 4 markers on each arm, and
Supplementary Figure S1: Anterior and posterior views of the marker set used in the running gait trials. Forty-six markers were attached to the subject (15 markers on each leg, 4 markers on each arm, and
INTERACTION OF STEP LENGTH AND STEP RATE DURING SPRINT RUNNING
 INTERACTION OF STEP LENGTH AND STEP RATE DURING SPRINT RUNNING Joseph P. Hunter 1, Robert N. Marshall 1,, and Peter J. McNair 3 1 Department of Sport and Exercise Science, The University of Auckland, Auckland,
INTERACTION OF STEP LENGTH AND STEP RATE DURING SPRINT RUNNING Joseph P. Hunter 1, Robert N. Marshall 1,, and Peter J. McNair 3 1 Department of Sport and Exercise Science, The University of Auckland, Auckland,
Purpose. Outline. Angle definition. Objectives:
 Disclosure Information AACPDM 69 th Annual Meeting October 21-24, 2015 Speaker Names: Sylvia Õunpuu, MSc and Kristan Pierz, MD Gait Analysis Data Interpretation: Understanding Kinematic Relationships Within
Disclosure Information AACPDM 69 th Annual Meeting October 21-24, 2015 Speaker Names: Sylvia Õunpuu, MSc and Kristan Pierz, MD Gait Analysis Data Interpretation: Understanding Kinematic Relationships Within
The technique of reciprocal walking using the hip guidance orthosis (hgo) with crutches
 The technique of reciprocal walking using the hip guidance orthosis (hgo) with crutches P. B. BUTLER, R. E. MAJOR and J. H. PATRICK Orthotic Research and Locomotor Assessment Unit, The Robert Jones and
The technique of reciprocal walking using the hip guidance orthosis (hgo) with crutches P. B. BUTLER, R. E. MAJOR and J. H. PATRICK Orthotic Research and Locomotor Assessment Unit, The Robert Jones and
Human hoppers compensate for simultaneous changes in surface compression and damping
 Journal of Biomechanics 39 (2006) 1030 1038 www.elsevier.com/locate/jbiomech www.jbiomech.com Human hoppers compensate for simultaneous changes in surface compression and damping Chet T. Moritz a,b,, Claire
Journal of Biomechanics 39 (2006) 1030 1038 www.elsevier.com/locate/jbiomech www.jbiomech.com Human hoppers compensate for simultaneous changes in surface compression and damping Chet T. Moritz a,b,, Claire
Lesson 14: Simple harmonic motion, Waves (Sections )
 Circular Motion and Simple Harmonic Motion The projection of uniform circular motion along any ais (the -ais here) is the same as simple harmonic motion. We use our understanding of uniform circular motion
Circular Motion and Simple Harmonic Motion The projection of uniform circular motion along any ais (the -ais here) is the same as simple harmonic motion. We use our understanding of uniform circular motion
Artifacts Due to Filtering Mismatch in Drop Landing Moment Data
 Camenga et al. UW-L Journal of Undergraduate Research XVI (213) Artifacts Due to Filtering Mismatch in Drop Landing Moment Data Elizabeth T. Camenga, Casey J. Rutten, Brendan D. Gould, Jillian T. Asmus,
Camenga et al. UW-L Journal of Undergraduate Research XVI (213) Artifacts Due to Filtering Mismatch in Drop Landing Moment Data Elizabeth T. Camenga, Casey J. Rutten, Brendan D. Gould, Jillian T. Asmus,
Gait Analyser. Description of Walking Performance
 Gait Analyser Description of Walking Performance This brochure will help you to understand clearly the parameters described in the report of the Gait Analyser, provide you with tips to implement the walking
Gait Analyser Description of Walking Performance This brochure will help you to understand clearly the parameters described in the report of the Gait Analyser, provide you with tips to implement the walking
Inertial compensation for belt acceleration in an instrumented treadmill
 Inertial compensation for belt acceleration in an instrumented treadmill Sandra K. Hnat, Antonie J. van den Bogert Department of Mechanical Engineering, Cleveland State University Cleveland, OH 44115,
Inertial compensation for belt acceleration in an instrumented treadmill Sandra K. Hnat, Antonie J. van den Bogert Department of Mechanical Engineering, Cleveland State University Cleveland, OH 44115,
Humanoid Robots and biped locomotion. Contact: Egidio Falotico
 Humanoid Robots and biped locomotion Contact: Egidio Falotico e.falotico@sssup.it Outline What is a Humanoid? Why Develop Humanoids? Challenges in Humanoid robotics Active vs Passive Locomotion Active
Humanoid Robots and biped locomotion Contact: Egidio Falotico e.falotico@sssup.it Outline What is a Humanoid? Why Develop Humanoids? Challenges in Humanoid robotics Active vs Passive Locomotion Active
The Influence of Load Carrying Modes on Gait variables of Healthy Indian Women
 The Influence of Load Carrying Modes on Gait variables of Healthy Indian Women *Guha Thakurta A, Iqbal R and De A National Institute of Industrial Engineering, Powai, Vihar Lake, Mumbai-400087, India,
The Influence of Load Carrying Modes on Gait variables of Healthy Indian Women *Guha Thakurta A, Iqbal R and De A National Institute of Industrial Engineering, Powai, Vihar Lake, Mumbai-400087, India,
Ball impact dynamics of knuckling shot in soccer
 Available online at www.sciencedirect.com Procedia Engineering 34 (2012 ) 200 205 9 th Conference of the International Sports Engineering Association (ISEA) Ball impact dynamics of knuckling shot in soccer
Available online at www.sciencedirect.com Procedia Engineering 34 (2012 ) 200 205 9 th Conference of the International Sports Engineering Association (ISEA) Ball impact dynamics of knuckling shot in soccer
A Biomechanical Approach to Javelin. Blake Vajgrt. Concordia University. December 5 th, 2012
 A Biomechanical Approach to Javelin Blake Vajgrt Concordia University December 5 th, 2012 The Biomechanical Approach to Javelin 2 The Biomechanical Approach to Javelin Javelin is one of the four throwing
A Biomechanical Approach to Javelin Blake Vajgrt Concordia University December 5 th, 2012 The Biomechanical Approach to Javelin 2 The Biomechanical Approach to Javelin Javelin is one of the four throwing
A New Approach to Modeling Vertical Stiffness in Heel-Toe Distance Runners
 Brigham Young University BYU ScholarsArchive All Faculty Publications 2003-12-01 A New Approach to Modeling Vertical Stiffness in Heel-Toe Distance Runners Iain Hunter iain_hunter@byu.edu Follow this and
Brigham Young University BYU ScholarsArchive All Faculty Publications 2003-12-01 A New Approach to Modeling Vertical Stiffness in Heel-Toe Distance Runners Iain Hunter iain_hunter@byu.edu Follow this and
Joint Torque Evaluation of Lower Limbs in Bicycle Pedaling
 11th conference of the International Sports Engineering Association, ISEA 216 Delft University of Technology; July 12 th Joint Torque Evaluation of Lower Limbs in Bicycle Pedaling Hiroki Yamazaki Akihiro
11th conference of the International Sports Engineering Association, ISEA 216 Delft University of Technology; July 12 th Joint Torque Evaluation of Lower Limbs in Bicycle Pedaling Hiroki Yamazaki Akihiro
Neurorehabil Neural Repair Oct 23. [Epub ahead of print]
![Neurorehabil Neural Repair Oct 23. [Epub ahead of print] Neurorehabil Neural Repair Oct 23. [Epub ahead of print]](/thumbs/86/94477916.jpg) APPENDICE Neurorehabil Neural Repair. 2009 Oct 23. [Epub ahead of print] Segmental Muscle Vibration Improves Walking in Chronic Stroke Patients With Foot Drop: A Randomized Controlled Trial. Paoloni M,
APPENDICE Neurorehabil Neural Repair. 2009 Oct 23. [Epub ahead of print] Segmental Muscle Vibration Improves Walking in Chronic Stroke Patients With Foot Drop: A Randomized Controlled Trial. Paoloni M,
Biomechanics Sample Problems
 Biomechanics Sample Problems Forces 1) A 90 kg ice hockey player collides head on with an 80 kg ice hockey player. If the first person exerts a force of 450 N on the second player, how much force does
Biomechanics Sample Problems Forces 1) A 90 kg ice hockey player collides head on with an 80 kg ice hockey player. If the first person exerts a force of 450 N on the second player, how much force does
How Do You Swing? You should be working with new lab partners starting with this lab.
 You should be working with new lab partners starting with this lab. Exploration: Swinging your arms and legs back and forth Discuss and try out the following questions within your lab group. After you
You should be working with new lab partners starting with this lab. Exploration: Swinging your arms and legs back and forth Discuss and try out the following questions within your lab group. After you
Equine Cannon Angle System
 Equine Cannon System How to interpret the results December 2010 Page 1 of 14 Table of Contents Introduction... 3 The Sagittal Plane... 4 The Coronal Plane... 5 Results Format... 6 How to Interpret the
Equine Cannon System How to interpret the results December 2010 Page 1 of 14 Table of Contents Introduction... 3 The Sagittal Plane... 4 The Coronal Plane... 5 Results Format... 6 How to Interpret the
Walking Simulator Mechanism
 The Downtown Review Volume 2 Issue 2 Article 4 2015 Walking Simulator Mechanism Titus Lungu Cleveland State University Igor Tachynskyy Cleveland State University Omri Tayyara Cleveland State University
The Downtown Review Volume 2 Issue 2 Article 4 2015 Walking Simulator Mechanism Titus Lungu Cleveland State University Igor Tachynskyy Cleveland State University Omri Tayyara Cleveland State University
Serve the only stroke in which the player has full control over its outcome. Bahamonde (2000) The higher the velocity, the smaller the margin of
 Lower Extremity Performance of Tennis Serve Reporter: Chin-Fu Hsu Adviser: Lin-Hwa Wang OUTLINE Introduction Kinetic Chain Serve Types Lower Extremity Movement Summary Future Work INTRODUCTION Serve the
Lower Extremity Performance of Tennis Serve Reporter: Chin-Fu Hsu Adviser: Lin-Hwa Wang OUTLINE Introduction Kinetic Chain Serve Types Lower Extremity Movement Summary Future Work INTRODUCTION Serve the
Steffen Willwacher, Katina Fischer, Gert Peter Brüggemann Institute of Biomechanics and Orthopaedics, German Sport University, Cologne, Germany
 P01-3 ID126 SURFACE STIFFNESS AFFECTS JOINT LOADING IN RUNNING Steffen Willwacher, Katina Fischer, Gert Peter Brüggemann Institute of Biomechanics and Orthopaedics, German Sport University, Cologne, Germany
P01-3 ID126 SURFACE STIFFNESS AFFECTS JOINT LOADING IN RUNNING Steffen Willwacher, Katina Fischer, Gert Peter Brüggemann Institute of Biomechanics and Orthopaedics, German Sport University, Cologne, Germany
by Michael Young Human Performance Consulting
 by Michael Young Human Performance Consulting The high performance division of USATF commissioned research to determine what variables were most critical to success in the shot put The objective of the
by Michael Young Human Performance Consulting The high performance division of USATF commissioned research to determine what variables were most critical to success in the shot put The objective of the
EXSC 408L Fall '03 Problem Set #2 Linear Motion. Linear Motion
 Problems: 1. Once you have recorded the calibration frame for a data collection, why is it important to make sure the camera does not shut off? hat happens if the camera automatically shuts off after being
Problems: 1. Once you have recorded the calibration frame for a data collection, why is it important to make sure the camera does not shut off? hat happens if the camera automatically shuts off after being
USA Track & Field Heptathlon Summit- November
 USA Track & Field Heptathlon Summit- November 1994 1 I. Technical considerations in the sprint hurdles Practical Biomechanics For the 100m Hurdles By Gary Winckler University of Illinois A. General flow
USA Track & Field Heptathlon Summit- November 1994 1 I. Technical considerations in the sprint hurdles Practical Biomechanics For the 100m Hurdles By Gary Winckler University of Illinois A. General flow
The Block Start and Accerlartion. Loren Seagrave Director of Track & Field and Cross Country Director of Speed and Movement
 The Block Start and Accerlartion Loren Seagrave Director of Track & Field and Cross Country Director of Speed and Movement Phases of Acceleration (Linear) The Start Greatest Rate of Acceleration Pure Acceleration
The Block Start and Accerlartion Loren Seagrave Director of Track & Field and Cross Country Director of Speed and Movement Phases of Acceleration (Linear) The Start Greatest Rate of Acceleration Pure Acceleration
Walking with coffee: when and why coffee spills
 Walking with coffee: when and why coffee spills Hans C. Mayer and Rouslan Krechetnikov Department of Mechanical Engineering University of California at Santa Barbara February 20-24, 2012 Page 1/25 Motivation
Walking with coffee: when and why coffee spills Hans C. Mayer and Rouslan Krechetnikov Department of Mechanical Engineering University of California at Santa Barbara February 20-24, 2012 Page 1/25 Motivation
Mutual and asynchronous anticipation and action in sports as globally competitive
 1 Supplementary Materials Mutual and asynchronous anticipation and action in sports as globally competitive and locally coordinative dynamics Keisuke Fujii, Tadao Isaka, Motoki Kouzaki and Yuji Yamamoto.
1 Supplementary Materials Mutual and asynchronous anticipation and action in sports as globally competitive and locally coordinative dynamics Keisuke Fujii, Tadao Isaka, Motoki Kouzaki and Yuji Yamamoto.
Development of a load model for men-induced loads on stairs
 Porto, Portugal, 30 June - 2 July 2014 A. Cunha, E. Caetano, P. Ribeiro, G. Müller (eds.) ISSN: 2311-9020; ISBN: 978-972-752-165-4 Development of a load model for men-induced loads on stairs Benjamin Czwikla
Porto, Portugal, 30 June - 2 July 2014 A. Cunha, E. Caetano, P. Ribeiro, G. Müller (eds.) ISSN: 2311-9020; ISBN: 978-972-752-165-4 Development of a load model for men-induced loads on stairs Benjamin Czwikla
Putting Report Details: Key and Diagrams: This section provides a visual diagram of the. information is saved in the client s database
 Quintic Putting Report Information Guide Putting Report Details: Enter personal details of the client or individual who is being analysed; name, email address, date, mass, height and handicap. This information
Quintic Putting Report Information Guide Putting Report Details: Enter personal details of the client or individual who is being analysed; name, email address, date, mass, height and handicap. This information
Mobility Lab provides sensitive, valid and reliable outcome measures.
 Mobility Lab provides sensitive, valid and reliable outcome measures. ith hundreds of universities and hospitals using this system worldwide, Mobility Lab is the most trusted wearable gait and balance
Mobility Lab provides sensitive, valid and reliable outcome measures. ith hundreds of universities and hospitals using this system worldwide, Mobility Lab is the most trusted wearable gait and balance
THE ANKLE-HIP TRANSVERSE PLANE COUPLING DURING THE STANCE PHASE OF NORMAL WALKING
 THE ANKLE-HIP TRANSVERSE PLANE COUPLING DURING THE STANCE PHASE OF NORMAL WALKING Thales R. Souza, Rafael Z. Pinto, Renato G. Trede, Nadja C. Pereira, Renata N. Kirkwood and Sérgio T. Fonseca. Movement
THE ANKLE-HIP TRANSVERSE PLANE COUPLING DURING THE STANCE PHASE OF NORMAL WALKING Thales R. Souza, Rafael Z. Pinto, Renato G. Trede, Nadja C. Pereira, Renata N. Kirkwood and Sérgio T. Fonseca. Movement
Friction properties of the face of a hand-held tennis racket
 Available online at www.sciencedirect.com Procedia Engineering 34 (2012 ) 544 549 9 th Conference of the International Sports Engineering Association (ISEA) Friction properties of the face of a hand-held
Available online at www.sciencedirect.com Procedia Engineering 34 (2012 ) 544 549 9 th Conference of the International Sports Engineering Association (ISEA) Friction properties of the face of a hand-held
REPORT. A comparative study of the mechanical and biomechanical behaviour of natural turf and hybrid turf for the practise of sports
 REPORT A comparative study of the mechanical and biomechanical behaviour of natural turf and hybrid turf for the practise of sports Addressed to: PSF - PALAU TURF Date: May 2015 Table of Contents SHEET
REPORT A comparative study of the mechanical and biomechanical behaviour of natural turf and hybrid turf for the practise of sports Addressed to: PSF - PALAU TURF Date: May 2015 Table of Contents SHEET
Posture influences ground reaction force: implications for crouch gait
 University of Tennessee, Knoxville From the SelectedWorks of Jeffrey A. Reinbolt July 14, 2010 Posture influences ground reaction force: implications for crouch gait H. X. Hoang Jeffrey A. Reinbolt, University
University of Tennessee, Knoxville From the SelectedWorks of Jeffrey A. Reinbolt July 14, 2010 Posture influences ground reaction force: implications for crouch gait H. X. Hoang Jeffrey A. Reinbolt, University
The overarching aim of the work presented in this thesis was to assess and
 CHAPTER 7 EPILOGUE Chapter 7 The overarching aim of the work presented in this thesis was to assess and understand the effort for balance control in terms of the metabolic cost of walking in able-bodied
CHAPTER 7 EPILOGUE Chapter 7 The overarching aim of the work presented in this thesis was to assess and understand the effort for balance control in terms of the metabolic cost of walking in able-bodied
Sample Solution for Problem 1.a
 Sample Solution for Problem 1.a 1 Inverted Pendulum Model (IPM) 1.1 Equations of Motion and Ground Reaction Forces Figure 1: Scheme of the Inverted Pendulum Model (IPM). The equations of motion of this
Sample Solution for Problem 1.a 1 Inverted Pendulum Model (IPM) 1.1 Equations of Motion and Ground Reaction Forces Figure 1: Scheme of the Inverted Pendulum Model (IPM). The equations of motion of this
Mechanics and energetics of level walking with powered ankle exoskeletons
 142 The Journal of Experimental Biology 211, 142-1413 Published by The Company of Biologists 28 doi:1.1242/jeb.9241 Mechanics and energetics of level walking with ed ankle exoskeletons Gregory S. Sawicki
142 The Journal of Experimental Biology 211, 142-1413 Published by The Company of Biologists 28 doi:1.1242/jeb.9241 Mechanics and energetics of level walking with ed ankle exoskeletons Gregory S. Sawicki
Dynamically stepping over large obstacle utilizing PSO optimization in the B4LC system
 1 Dynamically stepping over large obstacle utilizing PSO optimization in the B4LC system QI LIU, JIE ZHAO, KARSTEN BERNS Robotics Research Lab, University of Kaiserslautern, Kaiserslautern, 67655, Germany
1 Dynamically stepping over large obstacle utilizing PSO optimization in the B4LC system QI LIU, JIE ZHAO, KARSTEN BERNS Robotics Research Lab, University of Kaiserslautern, Kaiserslautern, 67655, Germany
ZMP Trajectory Generation for Reduced Trunk Motions of Biped Robots
 ZMP Trajectory Generation for Reduced Trunk Motions of Biped Robots Jong H. Park School of Mechanical Engineering Hanyang University Seoul, 33-79, Korea email:jong.park@ieee.org Yong K. Rhee School of
ZMP Trajectory Generation for Reduced Trunk Motions of Biped Robots Jong H. Park School of Mechanical Engineering Hanyang University Seoul, 33-79, Korea email:jong.park@ieee.org Yong K. Rhee School of
Muscle force redistributes segmental power for body progression during walking
 Gait and Posture 19 (2004) 194 205 Muscle force redistributes segmental power for body progression during walking R.R. Neptune a,b,, F.E. Zajac b,c,d, S.A. Kautz b,e,f,g a Department of Mechanical Engineering,
Gait and Posture 19 (2004) 194 205 Muscle force redistributes segmental power for body progression during walking R.R. Neptune a,b,, F.E. Zajac b,c,d, S.A. Kautz b,e,f,g a Department of Mechanical Engineering,
Toward a Human-like Biped Robot with Compliant Legs
 Book Title Book Editors IOS Press, 23 1 Toward a Human-like Biped Robot with Compliant Legs Fumiya Iida a,b,1, Yohei Minekawa a Juergen Rummel a and Andre Seyfarth a a Locomotion Laboratory, University
Book Title Book Editors IOS Press, 23 1 Toward a Human-like Biped Robot with Compliant Legs Fumiya Iida a,b,1, Yohei Minekawa a Juergen Rummel a and Andre Seyfarth a a Locomotion Laboratory, University
Equation 1: F spring = kx. Where F is the force of the spring, k is the spring constant and x is the displacement of the spring. Equation 2: F = mg
 1 Introduction Relationship between Spring Constant and Length of Bungee Cord In this experiment, we aimed to model the behavior of the bungee cord that will be used in the Bungee Challenge. Specifically,
1 Introduction Relationship between Spring Constant and Length of Bungee Cord In this experiment, we aimed to model the behavior of the bungee cord that will be used in the Bungee Challenge. Specifically,
Discus Technical Model
 Discus Technical Model Progression related to Multi-Events Development (aged 8/9-12 years) can be referenced to Athletics 365 stages Red, Yellow & Green Whole Sequence Preparation Momentum Building Delivery
Discus Technical Model Progression related to Multi-Events Development (aged 8/9-12 years) can be referenced to Athletics 365 stages Red, Yellow & Green Whole Sequence Preparation Momentum Building Delivery
EXPERIMENTAL STUDY OF EXOSKELETON FOR ANKLE AND KNEE JOINT
 EXPERIMENTAL STUDY OF EXOSKELETON FOR ANKLE AND KNEE JOINT PROJECT REFERENCE NO. : 37S0925 COLLEGE : NEW HORIZON COLLEGE OF ENGINEERING, BANGALORE BRANCH : MECHANICAL ENGINEERING GUIDES : DR GANESHA PRASAD
EXPERIMENTAL STUDY OF EXOSKELETON FOR ANKLE AND KNEE JOINT PROJECT REFERENCE NO. : 37S0925 COLLEGE : NEW HORIZON COLLEGE OF ENGINEERING, BANGALORE BRANCH : MECHANICAL ENGINEERING GUIDES : DR GANESHA PRASAD
Nature Neuroscience: doi: /nn Supplementary Figure 1. Visual responses of the recorded LPTCs
 Supplementary Figure 1 Visual responses of the recorded LPTCs (a) The mean±sd (n=3 trials) of the direction-selective (DS) responses (i.e., subtracting the null direction, ND, from the preferred direction,
Supplementary Figure 1 Visual responses of the recorded LPTCs (a) The mean±sd (n=3 trials) of the direction-selective (DS) responses (i.e., subtracting the null direction, ND, from the preferred direction,
ITTC Recommended Procedures and Guidelines
 Page 1 of 6 Table of Contents 1. PURPOSE...2 2. PARAMETERS...2 2.1 General Considerations...2 3 DESCRIPTION OF PROCEDURE...2 3.1 Model Design and Construction...2 3.2 Measurements...3 3.5 Execution of
Page 1 of 6 Table of Contents 1. PURPOSE...2 2. PARAMETERS...2 2.1 General Considerations...2 3 DESCRIPTION OF PROCEDURE...2 3.1 Model Design and Construction...2 3.2 Measurements...3 3.5 Execution of
In memory of Dr. Kevin P. Granata, my graduate advisor, who was killed protecting others on the morning of April 16, 2007.
 Acknowledgement In memory of Dr. Kevin P. Granata, my graduate advisor, who was killed protecting others on the morning of April 16, 2007. There are many others without whom I could not have completed
Acknowledgement In memory of Dr. Kevin P. Granata, my graduate advisor, who was killed protecting others on the morning of April 16, 2007. There are many others without whom I could not have completed
A Pilot Study on Electromyographic Analysis of Single and Double Revolution Jumps in Figure Skating
 Journal of Exercise Science and Physiotherapy, Vol. 5, No. 1: 14-19, 2009 A Pilot Study on Electromyographic Analysis of Single and Double Revolution Jumps in Figure Skating Taylor¹, C. L. and Psycharakis²,
Journal of Exercise Science and Physiotherapy, Vol. 5, No. 1: 14-19, 2009 A Pilot Study on Electromyographic Analysis of Single and Double Revolution Jumps in Figure Skating Taylor¹, C. L. and Psycharakis²,
Once-per-step control of ankle-foot prosthesis push-off work reduces effort associated with balance during walking
 Kim et al. Journal of NeuroEngineering and Rehabilitation (2015) 12:43 DOI 10.1186/s12984-015-0027-3 JOURNAL OF NEUROENGINEERING JNERAND REHABILITATION RESEARCH Open Access Once-per-step control of ankle-foot
Kim et al. Journal of NeuroEngineering and Rehabilitation (2015) 12:43 DOI 10.1186/s12984-015-0027-3 JOURNAL OF NEUROENGINEERING JNERAND REHABILITATION RESEARCH Open Access Once-per-step control of ankle-foot
UvA-DARE (Digital Academic Repository) Hip and groin pain in athletes Tak, I.J.R. Link to publication
 UvA-DARE (Digital Academic Repository) Hip and groin pain in athletes Tak, I.J.R. Link to publication Citation for published version (APA): Tak, I. J. R. (2017). Hip and groin pain in athletes: Morphology,
UvA-DARE (Digital Academic Repository) Hip and groin pain in athletes Tak, I.J.R. Link to publication Citation for published version (APA): Tak, I. J. R. (2017). Hip and groin pain in athletes: Morphology,
HOW DO WE ACCELERATE WHILE RUNNING? Daniel J. Schuster. April 2015
 HOW DO WE ACCELERATE WHILE RUNNING? by Daniel J. Schuster April 2015 Director of Thesis: Dr. Paul DeVita Major Department: Kinesiology Running biomechanics are well established in terms of lower extremity
HOW DO WE ACCELERATE WHILE RUNNING? by Daniel J. Schuster April 2015 Director of Thesis: Dr. Paul DeVita Major Department: Kinesiology Running biomechanics are well established in terms of lower extremity
Steeplechase Hurdle Economy, Mechanics, and Performance
 Brigham Young University BYU ScholarsArchive All Theses and Dissertations 2013-06-27 Steeplechase Hurdle Economy, Mechanics, and Performance Sarah Ingebretsen Brigham Young University - Provo Follow this
Brigham Young University BYU ScholarsArchive All Theses and Dissertations 2013-06-27 Steeplechase Hurdle Economy, Mechanics, and Performance Sarah Ingebretsen Brigham Young University - Provo Follow this
Complex movement patterns of a bipedal walk
 1 Complex movement patterns of a bipedal walk Objectives After completing this lesson, you will be able to: Describe the complex movement patterns of a bipedal walk. Describe the biomechanics of walking
1 Complex movement patterns of a bipedal walk Objectives After completing this lesson, you will be able to: Describe the complex movement patterns of a bipedal walk. Describe the biomechanics of walking
DIFFERENCE BETWEEN TAEKWONDO ROUNDHOUSE KICK EXECUTED BY THE FRONT AND BACK LEG - A BIOMECHANICAL STUDY
 268 Isas 2000! Hong Kong DIFFERENCE BETWEEN TAEKWONDO ROUNDHOUSE KICK EXECUTED BY THE FRONT AND BACK LEG - A BIOMECHANICAL STUDY Pui-Wah Kong, Tze-Chung Luk and Youlian Hong The Chinese University of Hong
268 Isas 2000! Hong Kong DIFFERENCE BETWEEN TAEKWONDO ROUNDHOUSE KICK EXECUTED BY THE FRONT AND BACK LEG - A BIOMECHANICAL STUDY Pui-Wah Kong, Tze-Chung Luk and Youlian Hong The Chinese University of Hong
The metabolic cost of human running: is swinging the arms worth it?
 214. Published by The Company of Biologists Ltd (214) 217, 2456-2461 doi:1.1242/jeb.142 RESEARCH ARTICLE The metabolic cost of human running: is swinging the arms worth it? Christopher J. Arellano 1,2,
214. Published by The Company of Biologists Ltd (214) 217, 2456-2461 doi:1.1242/jeb.142 RESEARCH ARTICLE The metabolic cost of human running: is swinging the arms worth it? Christopher J. Arellano 1,2,
ITF Coaches Education Programme Coaching High Performance Players Course Power and the Tennis Serve.
 ITF Coaches Education Programme Coaching High Performance Players Course Power and the Tennis Serve. By Machar Reid & Miguel Crespo A Powerful Serve A Key Ingredient of Successful Tennis Performance Preparation
ITF Coaches Education Programme Coaching High Performance Players Course Power and the Tennis Serve. By Machar Reid & Miguel Crespo A Powerful Serve A Key Ingredient of Successful Tennis Performance Preparation
Performance of three walking orthoses for the paralysed: a case study using gait analysis
 Prosthetics and Orthotics International, 1990, 14, 103 110 Performance of three walking orthoses for the paralysed: a case study using gait analysis R. J. JEFFERSON and M. W. WHITTLE Oxford Orthopaedic
Prosthetics and Orthotics International, 1990, 14, 103 110 Performance of three walking orthoses for the paralysed: a case study using gait analysis R. J. JEFFERSON and M. W. WHITTLE Oxford Orthopaedic
A COMPARISON OF SELECTED BIOMECHANICAL PARAMETERS OF FRONT ROW SPIKE BETWEEN SHORT SET AND HIGH SET BALL
 A COMPARISON OF SELECTED BIOMECHANICAL PARAMETERS OF FRONT ROW SPIKE BETWEEN SHORT SET AND HIGH SET BALL PAPAN MONDAL a AND SUDARSAN BHOWMICK b,* a Assistant Professor, Department of Physical Education,
A COMPARISON OF SELECTED BIOMECHANICAL PARAMETERS OF FRONT ROW SPIKE BETWEEN SHORT SET AND HIGH SET BALL PAPAN MONDAL a AND SUDARSAN BHOWMICK b,* a Assistant Professor, Department of Physical Education,
Investigation of Bio-Kinematic Elements of Three Point Shoot in Basketball
 International Journal of Sports Science 2017, 7(4): 163-169 DOI: 10.5923/j.sports.20170704.02 Investigation of Bio-Kinematic Elements of Three Point Shoot in Basketball Ikram Hussain, Fuzail Ahmad *, Nidhi
International Journal of Sports Science 2017, 7(4): 163-169 DOI: 10.5923/j.sports.20170704.02 Investigation of Bio-Kinematic Elements of Three Point Shoot in Basketball Ikram Hussain, Fuzail Ahmad *, Nidhi
Structure (Down plane)
 By Lauren Russell Structure (Down plane) The body (toes, knees, hips, wrists and shoulders) is aligned parallel to the intended target line. The torso is tilted over the ball from the hips whilst maintaining
By Lauren Russell Structure (Down plane) The body (toes, knees, hips, wrists and shoulders) is aligned parallel to the intended target line. The torso is tilted over the ball from the hips whilst maintaining
Locomotor Function of Forelimb Protractor and Retractor Muscles of Dogs: Evidence of Strut-like Behavior at the Shoulder
 University of South Florida Scholar Commons Integrative Biology Faculty and Staff Publications Integrative Biology 1-2008 Locomotor Function of Forelimb Protractor and Retractor Muscles of Dogs: Evidence
University of South Florida Scholar Commons Integrative Biology Faculty and Staff Publications Integrative Biology 1-2008 Locomotor Function of Forelimb Protractor and Retractor Muscles of Dogs: Evidence
Treadmill and daily life
 4 Treadmill and daily life Fall-related gait characteristics on the treadmill and in daily life, SM Rispens, JH van Dieën, KS van Schooten, LE Cofre Lizama, A Daffertshofer, PJ Beek, M Pijnappels, Journal
4 Treadmill and daily life Fall-related gait characteristics on the treadmill and in daily life, SM Rispens, JH van Dieën, KS van Schooten, LE Cofre Lizama, A Daffertshofer, PJ Beek, M Pijnappels, Journal
A QUALITATIVE ANALYSIS OF THE HIGH RACQUET POSITION BACKHAND DRIVE OF AN ELITE RACQUETBALL PLAYER
 A QUALITATIVE ANALYSIS OF THE HIGH RACQUET POSITION BACKHAND DRIVE OF AN ELITE RACQUETBALL PLAYER John R. Stevenson Wayne P. Hollander Since 1950, when Joe Sobek put strings on his paddleball paddle, the
A QUALITATIVE ANALYSIS OF THE HIGH RACQUET POSITION BACKHAND DRIVE OF AN ELITE RACQUETBALL PLAYER John R. Stevenson Wayne P. Hollander Since 1950, when Joe Sobek put strings on his paddleball paddle, the
HPW Biomechanics
 HPW Biomechanics hpw@mail.com www.hpwbiomechanics.com ~ via e-mail ~ January 31, 213 To: Attn: From: Subject: I-Roc Debbie Chapman Janet S. Dufek, Ph.D. Research Scientist Additional Footwear Evaluation
HPW Biomechanics hpw@mail.com www.hpwbiomechanics.com ~ via e-mail ~ January 31, 213 To: Attn: From: Subject: I-Roc Debbie Chapman Janet S. Dufek, Ph.D. Research Scientist Additional Footwear Evaluation
A NEW GOLF-SWING ROBOT MODEL UTILIZING SHAFT ELASTICITY
 Journal of Sound and Vibration (1998) 17(1), 17 31 Article No. sv981733 A NEW GOLF-SWING ROBOT MODEL UTILIZING SHAFT ELASTICITY S. SUZUKI Department of Mechanical System Engineering, Kitami Institute of
Journal of Sound and Vibration (1998) 17(1), 17 31 Article No. sv981733 A NEW GOLF-SWING ROBOT MODEL UTILIZING SHAFT ELASTICITY S. SUZUKI Department of Mechanical System Engineering, Kitami Institute of
ASSISTED AND RESISTED METHODS FOR SPEED DEVELOPMENT (PART 1)
 ASSISTED AND RESISTED METHODS FOR SPEED DEVELOPMENT (PART 1) By Adrian Faccioni Adrian Faccioni, a lecturer at the Centre of Sports Studies, University of Canberra, Australia, presents a detailed evaluation
ASSISTED AND RESISTED METHODS FOR SPEED DEVELOPMENT (PART 1) By Adrian Faccioni Adrian Faccioni, a lecturer at the Centre of Sports Studies, University of Canberra, Australia, presents a detailed evaluation
ScienceDirect. Rebounding strategies in basketball
 Available online at www.sciencedirect.com ScienceDirect Procedia Engineering 72 ( 2014 ) 823 828 The 2014 conference of the International Sports Engineering Association Rebounding strategies in basketball
Available online at www.sciencedirect.com ScienceDirect Procedia Engineering 72 ( 2014 ) 823 828 The 2014 conference of the International Sports Engineering Association Rebounding strategies in basketball
LocoMorph Deliverable 4.4 part 2.4
 LocoMorph Deliverable 4.4 part 2.4 Kinematics in healthy and morphosed long-tailed lizards (Takydromus sexlineatus): comparison of a simulation model with experimental animal data. Aim D Août K, Karakasiliotis
LocoMorph Deliverable 4.4 part 2.4 Kinematics in healthy and morphosed long-tailed lizards (Takydromus sexlineatus): comparison of a simulation model with experimental animal data. Aim D Août K, Karakasiliotis
Ground Reaction Forces and Lower Extremity Kinematics When Running With Suppressed Arm Swing
 Ground Reaction Forces and Lower Extremity Kinematics When Running With Suppressed Arm Swing Ross H. Miller 1 e-mail: rhmiller@kin.umass.edu Graham E. Caldwell Richard E. A. Van Emmerik Brian R. Umberger
Ground Reaction Forces and Lower Extremity Kinematics When Running With Suppressed Arm Swing Ross H. Miller 1 e-mail: rhmiller@kin.umass.edu Graham E. Caldwell Richard E. A. Van Emmerik Brian R. Umberger
Impact Points and Their Effect on Trajectory in Soccer
 Proceedings Impact Points and Their Effect on Trajectory in Soccer Kaoru Kimachi 1, *, Sungchan Hong 2, Shuji Shimonagata 3 and Takeshi Asai 2 1 Doctoral Program of Coaching Science, University of Tsukuba,
Proceedings Impact Points and Their Effect on Trajectory in Soccer Kaoru Kimachi 1, *, Sungchan Hong 2, Shuji Shimonagata 3 and Takeshi Asai 2 1 Doctoral Program of Coaching Science, University of Tsukuba,
Chs. 16 and 17 Mechanical Waves
 Chs. 16 and 17 Mechanical Waves The nature of waves A wave is a traveling disturbance that carries energy from one place to another, and even though matter may be disturbed as a wave travels through a
Chs. 16 and 17 Mechanical Waves The nature of waves A wave is a traveling disturbance that carries energy from one place to another, and even though matter may be disturbed as a wave travels through a
Kinematic Differences between Set- and Jump-Shot Motions in Basketball
 Proceedings Kinematic Differences between Set- and Jump-Shot Motions in Basketball Hiroki Okubo 1, * and Mont Hubbard 2 1 Department of Advanced Robotics, Chiba Institute of Technology, 2-17-1 Tsudanuma,
Proceedings Kinematic Differences between Set- and Jump-Shot Motions in Basketball Hiroki Okubo 1, * and Mont Hubbard 2 1 Department of Advanced Robotics, Chiba Institute of Technology, 2-17-1 Tsudanuma,
Denny Wells, Jacqueline Alderson, Kane Middleton and Cyril Donnelly
 11:45 am-12:00 pm Denny Wells. Assessing the accuracy of inverse kinematics in OpenSim to estimate elbow flexionextension during cricket bowling: Maintaining the rigid linked assumption. (201) ASSESSING
11:45 am-12:00 pm Denny Wells. Assessing the accuracy of inverse kinematics in OpenSim to estimate elbow flexionextension during cricket bowling: Maintaining the rigid linked assumption. (201) ASSESSING
Gait Analysis by High School Students
 Gait Analysis by High School Students André Heck 1 and Caroline van Dongen 2 1 AMSTEL Institute, University of Amsterdam, Amsterdam, The Netherlands, heck@science.uva.nl 2 St. Antoniuscollege, Gouda, The
Gait Analysis by High School Students André Heck 1 and Caroline van Dongen 2 1 AMSTEL Institute, University of Amsterdam, Amsterdam, The Netherlands, heck@science.uva.nl 2 St. Antoniuscollege, Gouda, The
Biomechanics of quadrupedal walking: how do four-legged animals achieve inverted pendulum-like movements?
 The Journal of Experimental Biology 27, 3545-3558 Published by The Company of Biologists 24 doi:1.1242/jeb.1177 3545 Biomechanics of quadrupedal walking: how do four-legged animals achieve inverted pendulum-like
The Journal of Experimental Biology 27, 3545-3558 Published by The Company of Biologists 24 doi:1.1242/jeb.1177 3545 Biomechanics of quadrupedal walking: how do four-legged animals achieve inverted pendulum-like
Ground Forces Impact on Release of Rotational Shot Put Technique
 Brigham Young University BYU ScholarsArchive All Theses and Dissertations 2014-12-01 Ground Forces Impact on Release of Rotational Shot Put Technique Niklas B. Arrhenius Brigham Young University - Provo
Brigham Young University BYU ScholarsArchive All Theses and Dissertations 2014-12-01 Ground Forces Impact on Release of Rotational Shot Put Technique Niklas B. Arrhenius Brigham Young University - Provo
SPRINTING CHARACTERISTICS OF WOMEN S 100 METER FINALS AT THE IAAF WORLD CHAMPIONSHOPS DAEGU 2011
 9:30-9:45 am Sang-Kyoon Park. Sprinting characteristics of women's 100 meter finals at the IAAF world championships Daegu 2011. (228) SPRINTING CHARACTERISTICS OF WOMEN S 100 METER FINALS AT THE IAAF WORLD
9:30-9:45 am Sang-Kyoon Park. Sprinting characteristics of women's 100 meter finals at the IAAF world championships Daegu 2011. (228) SPRINTING CHARACTERISTICS OF WOMEN S 100 METER FINALS AT THE IAAF WORLD
Biomechanical analysis of the medalists in the 10,000 metres at the 2007 World Championships in Athletics
 STUDY Biomechanical analysis of the medalists in the 10,000 metres at the 2007 World Championships in Athletics by IAAF 23:3; 61-66, 2008 By Yasushi Enomoto, Hirosuke Kadono, Yuta Suzuki, Tetsu Chiba,
STUDY Biomechanical analysis of the medalists in the 10,000 metres at the 2007 World Championships in Athletics by IAAF 23:3; 61-66, 2008 By Yasushi Enomoto, Hirosuke Kadono, Yuta Suzuki, Tetsu Chiba,
INTRODUCTION TO GAIT ANALYSIS DATA
 INTRODUCTION TO GAIT ANALYSIS DATA 1. Phases of gait a. Stance (% gc) i. Loading response (10%) ii. Mid- and terminal stance (%) iii. Pre-swing (10%) b. Swing (% gc) i. Initial swing ii. Mid-swing iii.
INTRODUCTION TO GAIT ANALYSIS DATA 1. Phases of gait a. Stance (% gc) i. Loading response (10%) ii. Mid- and terminal stance (%) iii. Pre-swing (10%) b. Swing (% gc) i. Initial swing ii. Mid-swing iii.
Variable Face Milling to Normalize Putter Ball Speed and Maximize Forgiveness
 Proceedings Variable Face Milling to Normalize Putter Ball Speed and Maximize Forgiveness Jacob Lambeth *, Dustin Brekke and Jeff Brunski Cleveland Golf, 5601 Skylab Rd. Huntington Beach, CA 92647, USA;
Proceedings Variable Face Milling to Normalize Putter Ball Speed and Maximize Forgiveness Jacob Lambeth *, Dustin Brekke and Jeff Brunski Cleveland Golf, 5601 Skylab Rd. Huntington Beach, CA 92647, USA;
