Unit 3 Day 7. Exponential Growth & Decay
|
|
|
- Arnold McDaniel
- 6 years ago
- Views:
Transcription
1 Unit 3 Day 7 Exponential Growth & Decay 1
2 Warm Up - Zombies SCENARIO 1 A pack of zombies is growing exponentially! After 1 hour, the original zombie infected 5 people, and those 5 zombies went on to infect 5 people, etc. After a zombie bite, it takes 1 hour to infect others. How many newly infected zombies will be created after 4 hours? If possible, draw a diagram, create a table, a graph, and an equation. SCENARIO 2 During this attack, a pack of 4 zombies walked into town last night around midnight. Each zombie infected 3 people total, and those 3 zombies went on to infect 3 people, etc. After a zombie bite, it takes an hour to infect others. Determine the number of newly infected zombies at 6 am this morning. If possible, draw a diagram, create a table, a graph, and an equation. SCENARIO 3 At 9:00 am, the official count of the zombie infestation was Every hour the number of zombies quadruples. Around what time did the first zombie roll into town? 2
3 New Zombies Time New Zombies y 5 x Time (hours) 3
4 New Zombies Time (hours) 4 Time New Zombies y 4(3) x
5 x 7 x 2AM Later in this unit, we ll learn how to solve these problems algebraically. For now, one way to solve is by using the calculator! Do y1 = 16384, y2 = (4) x then find intersection in calc. 5
6 Homework Answers Packet p odds & $4, 12 p x = 9 3. x = 4 4. No solution 5. x = 4 7. x = 2 9. x = 4 p x = x = a) h 9.8 ft. b) h 10.8 ft. c) h ft. 11. x = 7/2 6
7 Homework: Packet p. 12 & 13 Print Unit 3 Packet and Notes Days
8 Notes Day 7 Exponential Growth and Decay 8
9 What if??? You find a bank that will pay you 3% interest annually, so you consider moving your account, but, your current bank wants to keep you. They offer to compound semiannually! You get 2.5% interest and 1.25% interest at the end of June and 1% interest at the end of December. Which bank is giving you a better deal? We won t actually solve this problem but wouldn t it be nice to know how to in case you ran into a similar situation? Let s learn some about these types of problems today! 9
10 Review of Vocabulary Initial Value: The 1 st term in a sequence or the dependent value associated with an independent value of 0. Looking at Zombie Warm-up #2 During this attack, a pack of 4 zombies walked into town last night around midnight. Each zombie infected 3 people total, and those 3 zombies went on to infect 3 people, etc. Initial Value = 4 Common Ratio: The ratio of one term in a sequence and the previous term. Looking at Zombie Warm-up #2 Common Ratio = 3 Common Difference: The difference between one term in a sequence and the previous term. Looking at the sequence 4, 9, 14, 19, Common Difference = 5 10
11 Review of Vocabulary Recursive Function: a function that can be used to find any term in a sequence if you have the previous term (i.e. NOW-NEXT) Looking at Zombie Warm-up #2 During this attack, a pack of 4 zombies walked into town last night around midnight. Each zombie infected 3 people total, and those 3 zombies went on to infect 3 people, etc. Next = Now * 3 Start = 4 Explicit Function: a function that can be used to find any term in the sequence without having to know the previous term. (i.e. y = or f(x) = ) Looking at Zombie Warm-up #2 y = 4(3) x 11
12 Review of Vocabulary Domain: the set of all input values for a function Looking at Zombie Warm-up #2 y = 4(3) x the domain is all real numbers Theoretical Domain: the set of all input values for a function without consideration for context Looking at Zombie Warm-up #2 y = 4(3) x the theoretical domain is all real numbers Practical Domain: the set of all input values for a function that are reasonable within context Looking at Zombie Warm-up #2 y = 4(3) x the practical domain is x 0 because x is time in hours after 6 AM and it doesn t make sense to think about negative time We ll discuss these terms more later today!! 12
13 Note: Function is decreasing over time Note: Function is increasing over time 13
14 14
15 1 - r b = * r is the common ratio This is because you begin with 100% (1 when written as a decimal) and subtract the same percentage each time. 15
16 16
17 1 + r b = * r is the common ratio This is because you begin with 100% (1 when written as a decimal) and add the same percentage each time. 17
18 Examples 1. A house that costs $200,000 in 2010 will appreciate in value by 3% each year. a. Write a function that models the cost of the house over time. Use x for years after 2010, and y for the value of the house, in dollars. y b. Find the value of the house in $ 268, ,000(1.03) x c. In what year will the house value have doubled? Year 2033 More vocab you must know! *Appreciate means increasing rate *Depreciate means decreasing rate 18
19 Examples 2. The most recent virus that is making people ill is a fast multiplying one. On the first day of the illness, only 2 virus bugs are present. Each day after, the amount of bugs triples. a. Write a function that models the bugs growth over time. Let x represent the number of days since the onset of the illness and y represent the amount of bugs. y 2(3) x b. Find the amount of bugs present by the 5 th day. y 5 2(3) 486 bugs 19
20 Examples 3. You have a bad cough and have to attend your little sister s choir concert. You take cough drops that contain 100 mg of menthol in each drop. Every minute, the amount of menthol in your body is cut in half. a. Write a function that models the amount of menthol in your body over time. Let x represent minutes since you took the cough drops and y be the amount of menthol, in mg, remaining in your body. b. It is safe to take a new cough drop when the amount of menthol in your body is less than 5 mg. How long will it be before you can take another cough drop? y 100(1 1 ) 20 About 4.3 minutes 2 x More vocab you must know! *Half Life = Amount of time for a substance to be cut in half For this problem, the half life is 1 minute
21 Example! Let s try a tougher problem you may run in to! 4. You have a bad cough and have to attend your little sister s choir concert. You take cough drops that contain 100 mg of menthol in each drop. Every 5 minutes, the amount of menthol in your body is cut in half. Remember Half Life = Amount of time for a substance to be cut in half a. Write a function that models the amount of menthol in your body over time. Let x represent minutes since you took the cough drops and y be the amount of menthol, in mg, remaining in your body. y = 100(1/2) t/5 you must do t/5 exponent so that the exponent will determine the number of half lives that have occurred b. It is safe to take a new cough drop when the amount of menthol in your body is less than 5 mg. How long will it be before you can take another cough drop? 5 = 100(1/2) t/5 Do y1 = 5, y2 = 100(1/2) t/5 then find intersection in calc. 21
22 In the problems above, we wrote explicit functions for the exponential data. BUT we also need to know how to write recursive functions for the exponential data. Make sure you include the starting value of your data a this will always be where the independent variable is 0. Next = Now * b, Starting at a (You must tell the values of b and a) 22
23 Let s write the prior examples using Recursive Formulas! Next = Now * b, Starting at a 1. A house that costs $200,000 in 2010 will appreciate in value by 3% each year. Next = Now * 1.03, Start = 200, The most recent virus that is making people ill is a fast multiplying one. On the first day of the illness, only 2 virus bugs are present. Each day after, the amount of bugs triples. Next = Now * 3, Start = 2 3. You have a bad cough and have to attend your little sister s choir concert. You take cough drops that contain 100 mg of menthol in each drop. Every minute, the amount of menthol in your body is cut in half. Next = Now * 0.5, Start =
24 You Try # Tobias ate half a banana in his room and forgot to throw the rest away. That night, two gnats came to visit the banana. Each night after, there were four times as many gnats hanging around the banana. a. Write an explicit function that models the gnats grown over time. Use x for nights after you first see the gnats and y for number of gnats. y 2(4) x b. Tobias mom said that he would be grounded if the gnats number more than 120. On what night will Tobias be in trouble, if he doesn t step in and solve his gnat problem? x 120 2(4), so x 3 c. Write a recursive function to model the gnats growth. Next = Now * 4, Start = 2 24
25 You Try #5 5. JaCorren is 60 inches and going through a growth spurt. For the next year, his growth will increase by 1% each month. Let x represent number of months and y represent JaCorren s height in inches. a. Write an explicit function that models JaCorren s growth spurt over the next year. y 60(1.01) x y 60(1.01) x b. Find JaCorren s height at the end of the year. y 12 60(1.01) in. c. Write a recursive function to model JaCorren s growth. Next = Now * 1.01, Start = 60 25
26 You Try #6 6. Ian s new Mercedes cost him $75,000 in From the moment he drives it off the lot, it will depreciate by 20% each year for the first five years. a. Write an explicit function that models the car s depreciation. Use x for years after 2014 and y for the car s value, in dollars. y 75000(1.20) x y 75000(.80) x b. What will the car s value be in 2019? y (.80) $24,576 c. Write a recursive function to model the car s depreciation. Next = Now *.80, Start = 75,000 26
27 More on Theoretical and Practical Domain When you write an equation for a situation and use it to make predictions, you assume that other people who use it will understand the situation as well as you do. That s not always the case when you take away the context, so we sometimes need to provide some additional information to accompany the equation. The domain of a function is the set of all the possible input values that can be used when evaluating it. If you remove your functions from the context of this situation and simply look at the table and/or graph of the function, what numbers are part of the theoretical domain of the function? Will this be the case with all exponential functions? Why or why not? When you consider the context, however, not all of the numbers in the theoretical domain really make sense. We call the numbers in the theoretical domain that make sense in our situation the practical domain. If you look at the tables for the problems, we can find what numbers would be a part of the practical domain. 27
28 More on Theoretical and Practical Domain Let s find the theoretical domain and practical domain of some of the practice problems you just did. Together 4. Tobias ate half a banana in his room and forgot to throw the rest away. That night, two gnats came to visit the banana. Each night after, there were four times as many gnats hanging around the banana. You try 5. JaCorren is 60 inches and going through a growth spurt. For the next year, his growth will increase by 1% each month. Let x represent number of months and y represent JaCorren s height in inches. 28
29 Homework: Packet p. 12 & 13 Print Unit 3 Packet and Notes Days
30 Practice Exponential Word Problems Scavenger Hunt OR Additional Practice 30
Algebra I: A Fresh Approach. By Christy Walters
 Algebra I: A Fresh Approach By Christy Walters 2016 A+ Education Services All rights reserved. No part of this publication may be reproduced, distributed, stored in a retrieval system, or transmitted,
Algebra I: A Fresh Approach By Christy Walters 2016 A+ Education Services All rights reserved. No part of this publication may be reproduced, distributed, stored in a retrieval system, or transmitted,
Lesson 7: Exponential Decay
 Classwork Example 1 a. Malik bought a new car for $15,000. As he drove it off the lot, his best friend, Will, told him that the car s value just dropped by 15% and that it would continue to depreciate
Classwork Example 1 a. Malik bought a new car for $15,000. As he drove it off the lot, his best friend, Will, told him that the car s value just dropped by 15% and that it would continue to depreciate
Algebra I: A Fresh Approach. By Christy Walters
 Algebra I: A Fresh Approach By Christy Walters 2005 A+ Education Services All rights reserved. No part of this publication may be reproduced, distributed, stored in a retrieval system, or transmitted,
Algebra I: A Fresh Approach By Christy Walters 2005 A+ Education Services All rights reserved. No part of this publication may be reproduced, distributed, stored in a retrieval system, or transmitted,
Warm Up: Thursday, 11/5/2015
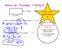 Warm Up: Thursday, 11/5/2015 5x inches (2x 4) inches Chapter 4 Section 1 All 1.) What is the perimeter of the rectangle? P = 2l + 2w 2.) What is the area of the rectangle? A = lw 2.) Look at note packets
Warm Up: Thursday, 11/5/2015 5x inches (2x 4) inches Chapter 4 Section 1 All 1.) What is the perimeter of the rectangle? P = 2l + 2w 2.) What is the area of the rectangle? A = lw 2.) Look at note packets
Warm Up: Thursday, 11/5/2015
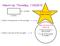 Warm Up: Thursday, 11/5/2015 5x inches (2x 4) inches Chapter 4 Section 1 1.) What is the perimeter of the rectangle? P = 2l + 2w 2.) What is the area of the rectangle? A = lw 2.) Look at note packets for
Warm Up: Thursday, 11/5/2015 5x inches (2x 4) inches Chapter 4 Section 1 1.) What is the perimeter of the rectangle? P = 2l + 2w 2.) What is the area of the rectangle? A = lw 2.) Look at note packets for
APPROVED FACILITY SCHOOLS CURRICULUM DOCUMENT SUBJECT: Mathematics GRADE: 6. TIMELINE: Quarter 1. Student Friendly Learning Objective
 TIMELINE: Quarter 1 i-ready lesson: Rational Numbers and Absolute Value i-ready lesson: Numerical Expressions and Order of Operations 6/16/15 1 i-ready lesson (2a, 2b and 2c): Algebraic Expressions 6/16/15
TIMELINE: Quarter 1 i-ready lesson: Rational Numbers and Absolute Value i-ready lesson: Numerical Expressions and Order of Operations 6/16/15 1 i-ready lesson (2a, 2b and 2c): Algebraic Expressions 6/16/15
B.U.G. Newsletter. Full Steam Ahead! September Dr. Brown
 B.U.G. Newsletter September 2014 THIS NEWSLETTER IS A SERVICE THAT WAS FUNDED BY "NO CHILD LEFT BEHIND" TITLE II PART A HIGHER EDUCATION IMPROVING TEACHER QUALITY HIGHER EDUCATION GRANT ADMINISTERED THROUGH
B.U.G. Newsletter September 2014 THIS NEWSLETTER IS A SERVICE THAT WAS FUNDED BY "NO CHILD LEFT BEHIND" TITLE II PART A HIGHER EDUCATION IMPROVING TEACHER QUALITY HIGHER EDUCATION GRANT ADMINISTERED THROUGH
When it is 80 degrees he will sell about 42 ice creams.
 What are some of the ways Functions are represented? Essential Question Essential Question Essential Question Essential Question Essential Question Essential Question Essential Question Week 4, Lesson
What are some of the ways Functions are represented? Essential Question Essential Question Essential Question Essential Question Essential Question Essential Question Essential Question Week 4, Lesson
LEARNING OBJECTIVES. Overview of Lesson. guided practice Teacher: anticipates, monitors, selects, sequences, and connects student work
 D Rate, Lesson 1, Conversions (r. 2018) RATE Conversions Common Core Standard N.Q.A.1 Use units as a way to understand problems and to guide the solution of multi-step problems; choose and interpret units
D Rate, Lesson 1, Conversions (r. 2018) RATE Conversions Common Core Standard N.Q.A.1 Use units as a way to understand problems and to guide the solution of multi-step problems; choose and interpret units
Math 4. Unit 1: Conic Sections Lesson 1.1: What Is a Conic Section?
 Unit 1: Conic Sections Lesson 1.1: What Is a Conic Section? 1.1.1: Study - What is a Conic Section? Duration: 50 min 1.1.2: Quiz - What is a Conic Section? Duration: 25 min / 18 Lesson 1.2: Geometry of
Unit 1: Conic Sections Lesson 1.1: What Is a Conic Section? 1.1.1: Study - What is a Conic Section? Duration: 50 min 1.1.2: Quiz - What is a Conic Section? Duration: 25 min / 18 Lesson 1.2: Geometry of
3. A shirt is priced at $32.00 now. If the shirt goes on sale for 30% off the current price, what will be the sale price of the shirt?
 1 Math 1 - Proportions & Probability Part 2 PERCENT INCREASE AND DECREASE To increase a number by a percent, add the percent to 100%, convert to a decimal, and multiply. To increase 40 by 25%, add 25%
1 Math 1 - Proportions & Probability Part 2 PERCENT INCREASE AND DECREASE To increase a number by a percent, add the percent to 100%, convert to a decimal, and multiply. To increase 40 by 25%, add 25%
Coimisiún na Scrúduithe Stáit State Examinations Commission. Junior Certificate Examination Mathematics
 2018. S34 Coimisiún na Scrúduithe Stáit State Examinations Commission Junior Certificate Examination 2018 Mathematics Paper 1 Higher Level Friday 8 June Afternoon 2:00 to 4:30 300 marks Examination Number
2018. S34 Coimisiún na Scrúduithe Stáit State Examinations Commission Junior Certificate Examination 2018 Mathematics Paper 1 Higher Level Friday 8 June Afternoon 2:00 to 4:30 300 marks Examination Number
Algebra Date Lesson Independent Work Computer Tuesday, Introduction (whole class) Problem with Dice
 Tuesday, Introduction (whole class) Problem with Dice Critical Thinking Puzzles 3 Station expectations Count the Squares Math Riddles Wednesday, Computer expectations (whole class) Tangrams Read permission
Tuesday, Introduction (whole class) Problem with Dice Critical Thinking Puzzles 3 Station expectations Count the Squares Math Riddles Wednesday, Computer expectations (whole class) Tangrams Read permission
Lesson 14: Modeling Relationships with a Line
 Exploratory Activity: Line of Best Fit Revisited 1. Use the link http://illuminations.nctm.org/activity.aspx?id=4186 to explore how the line of best fit changes depending on your data set. A. Enter any
Exploratory Activity: Line of Best Fit Revisited 1. Use the link http://illuminations.nctm.org/activity.aspx?id=4186 to explore how the line of best fit changes depending on your data set. A. Enter any
ASVAB Arithmetic Reasoning
 ASVAB Arithmetic Reasoning Number: Arithmetic Reasoning Passing Score: 800 Time Limit: 120 min File Version: 1.0 Arithmetic Reasoning QUESTION 1 If there are 3 quarts of gas in a gallon container, how
ASVAB Arithmetic Reasoning Number: Arithmetic Reasoning Passing Score: 800 Time Limit: 120 min File Version: 1.0 Arithmetic Reasoning QUESTION 1 If there are 3 quarts of gas in a gallon container, how
Algebra Date Lesson Independent Work Computer Tuesday, Introduction (whole class) Problem with Dice
 Tuesday, Introduction (whole class) Problem with Dice Critical Thinking Puzzles September 3 Station expectations Count the Squares Math Riddles Wednesday, Computer expectations (whole class) Tangrams Read
Tuesday, Introduction (whole class) Problem with Dice Critical Thinking Puzzles September 3 Station expectations Count the Squares Math Riddles Wednesday, Computer expectations (whole class) Tangrams Read
100-Meter Dash Olympic Winning Times: Will Women Be As Fast As Men?
 100-Meter Dash Olympic Winning Times: Will Women Be As Fast As Men? The 100 Meter Dash has been an Olympic event since its very establishment in 1896(1928 for women). The reigning 100-meter Olympic champion
100-Meter Dash Olympic Winning Times: Will Women Be As Fast As Men? The 100 Meter Dash has been an Olympic event since its very establishment in 1896(1928 for women). The reigning 100-meter Olympic champion
Bioequivalence: Saving money with generic drugs
 The Right Stuff: Appropriate Mathematics for All Students Promoting the use of materials that engage students in meaningful activities that promote the effective use of technology to support mathematics,
The Right Stuff: Appropriate Mathematics for All Students Promoting the use of materials that engage students in meaningful activities that promote the effective use of technology to support mathematics,
Fun with Folding. led by Thomas Clark. October 7, Take a strip of paper, fold it in half, and make a good crease at the midpoint position.
 Preliminary Folding Investigation Fun with Folding led by Thomas Clark October 7, 2014 1. Take a strip of paper, fold it in half, and make a good crease at the midpoint position. 2. Open up the strip,
Preliminary Folding Investigation Fun with Folding led by Thomas Clark October 7, 2014 1. Take a strip of paper, fold it in half, and make a good crease at the midpoint position. 2. Open up the strip,
Height (ft) Find the average rebound percentage for your ball. Show your work.
 Different balls bounce at various heights depending on things like the type of ball, the pressure of air in the ball, and the surface on which it is bounced. The rebound percentage of a ball is found by
Different balls bounce at various heights depending on things like the type of ball, the pressure of air in the ball, and the surface on which it is bounced. The rebound percentage of a ball is found by
Lesson 2 Pre-Visit Batting Average Ups and Downs
 Lesson 2 Pre-Visit Batting Average Ups and Downs Objective: Students will be able to: Use multiple data sets to determine the overall success rate of a particular activity. Select and create appropriate
Lesson 2 Pre-Visit Batting Average Ups and Downs Objective: Students will be able to: Use multiple data sets to determine the overall success rate of a particular activity. Select and create appropriate
Combining Unlike Integers
 Math, Lesson Lesson pp. 8- Lesson Preparation Drill Do Speed Drill and write the number correct in the blank. Speed Drill Combining Unlike Integers Unlike integers are both positive and negative numbers
Math, Lesson Lesson pp. 8- Lesson Preparation Drill Do Speed Drill and write the number correct in the blank. Speed Drill Combining Unlike Integers Unlike integers are both positive and negative numbers
77.1 Apply the Pythagorean Theorem
 Right Triangles and Trigonometry 77.1 Apply the Pythagorean Theorem 7.2 Use the Converse of the Pythagorean Theorem 7.3 Use Similar Right Triangles 7.4 Special Right Triangles 7.5 Apply the Tangent Ratio
Right Triangles and Trigonometry 77.1 Apply the Pythagorean Theorem 7.2 Use the Converse of the Pythagorean Theorem 7.3 Use Similar Right Triangles 7.4 Special Right Triangles 7.5 Apply the Tangent Ratio
Monday Tuesday Wednesday Thursday
 Name: Weekly Math Homework - Q1:1 Teacher: Monday Tuesday Wednesday Thursday Use Order of Operations to simplify. Use Order of Operations to simplify. Use Order of Operations to simplify. Use Order of
Name: Weekly Math Homework - Q1:1 Teacher: Monday Tuesday Wednesday Thursday Use Order of Operations to simplify. Use Order of Operations to simplify. Use Order of Operations to simplify. Use Order of
GRADE 8 BASELINE TEST 2013 MATHEMATICS. 1 Hour 30 Minutes
 GRADE 8 BASELINE TEST 2013 GRADE 8 BASELINE TEST MATHEMATICS 2013 MATHEMATICS 1 Hour 30 Minutes 1 Hour 30 Minutes SCHOOL:. LEARNER:.. CLASS: 1 Baseline Assessment Instrument Gr 8 (135 marks) Read the questions
GRADE 8 BASELINE TEST 2013 GRADE 8 BASELINE TEST MATHEMATICS 2013 MATHEMATICS 1 Hour 30 Minutes 1 Hour 30 Minutes SCHOOL:. LEARNER:.. CLASS: 1 Baseline Assessment Instrument Gr 8 (135 marks) Read the questions
MATH IN ACTION TABLE OF CONTENTS. Lesson 1.1 On Your Mark, Get Set, Go! Page: 10 Usain Bolt: The fastest man on the planet
 MATH IN ACTION TABLE OF CONTENTS LESSON 1 WORLD RECORD SPEEDS LINEAR FUNCTIONS WITH PROPORTIONAL RELATIONSHIPS Focus on: SLOPE Lesson 1.1 On Your Mark, Get Set, Go! Page: 10 Usain Bolt: The fastest man
MATH IN ACTION TABLE OF CONTENTS LESSON 1 WORLD RECORD SPEEDS LINEAR FUNCTIONS WITH PROPORTIONAL RELATIONSHIPS Focus on: SLOPE Lesson 1.1 On Your Mark, Get Set, Go! Page: 10 Usain Bolt: The fastest man
Height (ft) Find the average rebound percentage for your ball. Show your work.
 Different balls bounce at various heights depending on things like the type of ball, the pressure of air in the ball, and the surface on which it is bounced. The rebound percentage of a ball is found by
Different balls bounce at various heights depending on things like the type of ball, the pressure of air in the ball, and the surface on which it is bounced. The rebound percentage of a ball is found by
Simplifying Radical Expressions and the Distance Formula
 1 RD. Simplifying Radical Expressions and the Distance Formula In the previous section, we simplified some radical expressions by replacing radical signs with rational exponents, applying the rules of
1 RD. Simplifying Radical Expressions and the Distance Formula In the previous section, we simplified some radical expressions by replacing radical signs with rational exponents, applying the rules of
Mathematics. Leaving Certificate Examination Paper 1 Higher Level Friday 10 th June Afternoon 2:00 4:30
 2016. M29 Coimisiún na Scrúduithe Stáit State Examinations Commission Leaving Certificate Examination 2016 Mathematics Paper 1 Higher Level Friday 10 th June Afternoon 2:00 4:30 300 marks Examination number
2016. M29 Coimisiún na Scrúduithe Stáit State Examinations Commission Leaving Certificate Examination 2016 Mathematics Paper 1 Higher Level Friday 10 th June Afternoon 2:00 4:30 300 marks Examination number
Algebra Date Lesson Independent Work Computer Tuesday, Introduction (whole class) Problem with Dice
 Introduction (whole class) Problem with Dice Critical Thinking Puzzles 3 Station expectations Count the Squares Math Riddles Wednesday, Computer expectations (whole class) Tangrams Read permission slip
Introduction (whole class) Problem with Dice Critical Thinking Puzzles 3 Station expectations Count the Squares Math Riddles Wednesday, Computer expectations (whole class) Tangrams Read permission slip
March Madness Basketball Tournament
 March Madness Basketball Tournament Math Project COMMON Core Aligned Decimals, Fractions, Percents, Probability, Rates, Algebra, Word Problems, and more! To Use: -Print out all the worksheets. -Introduce
March Madness Basketball Tournament Math Project COMMON Core Aligned Decimals, Fractions, Percents, Probability, Rates, Algebra, Word Problems, and more! To Use: -Print out all the worksheets. -Introduce
Lesson 1 Pre-Visit Batting Average
 Lesson 1 Pre-Visit Batting Average Objective: Students will be able to: Calculate a batting average. Review prior knowledge of conversion between fractions, decimals, and percentages. Use basic linear
Lesson 1 Pre-Visit Batting Average Objective: Students will be able to: Calculate a batting average. Review prior knowledge of conversion between fractions, decimals, and percentages. Use basic linear
Grade: 8. Author(s): Hope Phillips
 Title: Tying Knots: An Introductory Activity for Writing Equations in Slope-Intercept Form Prior Knowledge Needed: Grade: 8 Author(s): Hope Phillips BIG Idea: Linear Equations how to analyze data from
Title: Tying Knots: An Introductory Activity for Writing Equations in Slope-Intercept Form Prior Knowledge Needed: Grade: 8 Author(s): Hope Phillips BIG Idea: Linear Equations how to analyze data from
4-3 Rate of Change and Slope. Warm Up Lesson Presentation. Lesson Quiz
 4-3 Rate of Change and Slope Warm Up Lesson Presentation Lesson Quiz Holt Algebra McDougal 1 Algebra 1 Warm Up 1. Find the x- and y-intercepts of 2x 5y = 20. x-int.: 10; y-int.: 4 Describe the correlation
4-3 Rate of Change and Slope Warm Up Lesson Presentation Lesson Quiz Holt Algebra McDougal 1 Algebra 1 Warm Up 1. Find the x- and y-intercepts of 2x 5y = 20. x-int.: 10; y-int.: 4 Describe the correlation
Lesson 2 Pre-Visit Slugging Percentage
 Lesson 2 Pre-Visit Slugging Percentage Objective: Students will be able to: Set up and solve equations for batting average and slugging percentage. Review prior knowledge of conversion between fractions,
Lesson 2 Pre-Visit Slugging Percentage Objective: Students will be able to: Set up and solve equations for batting average and slugging percentage. Review prior knowledge of conversion between fractions,
Extra: What is the minimum (fewest) number of train cars that it would take to hold all those passengers at once, if each car holds 12 passengers?
 Problem of the Week Teacher Packet Zoo Train The zoo has a train that carries people between exhibits. One morning the first passengers got on at Monkey House. At Alligator Pond the number of people who
Problem of the Week Teacher Packet Zoo Train The zoo has a train that carries people between exhibits. One morning the first passengers got on at Monkey House. At Alligator Pond the number of people who
University of Colorado-Boulder MATH 1300 Homework 1
 Turn in the following problems: 1. Consider the following mathematical statements. Determine if the statements are always true, sometimes true, or never true. (a) (x + 2) 4 = x 4 + 16 (b) x 4 + 8x 2 +
Turn in the following problems: 1. Consider the following mathematical statements. Determine if the statements are always true, sometimes true, or never true. (a) (x + 2) 4 = x 4 + 16 (b) x 4 + 8x 2 +
Essential Question Essential Question Essential Question Essential Question Essential Question Essential Question Essential Question
 Essential Question Essential Question Essential Question Essential Question Essential Question Essential Question Essential Question Week 11, Lesson 1 1. Warm up 2. Notes Review 3. ICA QUIZ 57 Warm up
Essential Question Essential Question Essential Question Essential Question Essential Question Essential Question Essential Question Week 11, Lesson 1 1. Warm up 2. Notes Review 3. ICA QUIZ 57 Warm up
Probability of an Ace in Disc Golf by stevewestdiscgolf.com April 18, 2011
 Probability of an Ace in Disc Golf by stevewestdiscgolf.com April 18, 2011 Data Ace Race Charlie Hutchinson of GottaGoGottaThrow ran an Ace Race in November, 2010. He was kind enough to measure the distances
Probability of an Ace in Disc Golf by stevewestdiscgolf.com April 18, 2011 Data Ace Race Charlie Hutchinson of GottaGoGottaThrow ran an Ace Race in November, 2010. He was kind enough to measure the distances
March Madness Basketball Tournament
 March Madness Basketball Tournament Math Project COMMON Core Aligned Decimals, Fractions, Percents, Probability, Rates, Algebra, Word Problems, and more! To Use: -Print out all the worksheets. -Introduce
March Madness Basketball Tournament Math Project COMMON Core Aligned Decimals, Fractions, Percents, Probability, Rates, Algebra, Word Problems, and more! To Use: -Print out all the worksheets. -Introduce
Graphing Stories Writing Equations
 Exploratory Activity Consider the story: Maya and Earl live at opposite ends of the hallway in their apartment building. Their doors are 50 ft. apart. Each starts at his or her own door and walks at a
Exploratory Activity Consider the story: Maya and Earl live at opposite ends of the hallway in their apartment building. Their doors are 50 ft. apart. Each starts at his or her own door and walks at a
Student Resource / Program Workbook INTEGERS
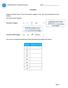 INTEGERS Integers are whole numbers. They can be positive, negative or zero. They cannot be decimals or most fractions. Let us look at some examples: Examples of integers: +4 0 9-302 Careful! This is a
INTEGERS Integers are whole numbers. They can be positive, negative or zero. They cannot be decimals or most fractions. Let us look at some examples: Examples of integers: +4 0 9-302 Careful! This is a
NAME BLOCK Density Lab PROBLEM: How can we determine the densities of different substances?
 NAME BLOCK Density Lab PROBLEM: How can we determine the densities of different substances? PART 1 Determining relative density procedure 1. Designate an eyedropper for each beaker. Do not mix them up
NAME BLOCK Density Lab PROBLEM: How can we determine the densities of different substances? PART 1 Determining relative density procedure 1. Designate an eyedropper for each beaker. Do not mix them up
100-Meter Dash Olympic Winning Times: Will Women Be As Fast As Men?
 100-Meter Dash Olympic Winning Times: Will Women Be As Fast As Men? The 100 Meter Dash has been an Olympic event since its very establishment in 1896(1928 for women). The reigning 100-meter Olympic champion
100-Meter Dash Olympic Winning Times: Will Women Be As Fast As Men? The 100 Meter Dash has been an Olympic event since its very establishment in 1896(1928 for women). The reigning 100-meter Olympic champion
Besides the reported poor performance of the candidates there were a number of mistakes observed on the assessment tool itself outlined as follows:
 MATHEMATICS (309/1) REPORT The 2013 Mathematics (309/1) paper was of average standard. The paper covered a wide range of the syllabus. It was neither gender bias nor culture bias. It did not have language
MATHEMATICS (309/1) REPORT The 2013 Mathematics (309/1) paper was of average standard. The paper covered a wide range of the syllabus. It was neither gender bias nor culture bias. It did not have language
GCSE 185/08 MATHEMATICS FOUNDATION TIER PAPER 2. A.M. THURSDAY, 17 November hours. Centre Number. Candidate Number. Surname.
 Surname Other Names Centre Number 0 Candidate Number GCSE 185/08 MATHEMATICS FOUNDATION TIER PAPER 2 A.M. THURSDAY, 17 November 2011 2 hours For s use Question Maximum Mark Mark Awarded ADDITIONAL MATERIALS
Surname Other Names Centre Number 0 Candidate Number GCSE 185/08 MATHEMATICS FOUNDATION TIER PAPER 2 A.M. THURSDAY, 17 November 2011 2 hours For s use Question Maximum Mark Mark Awarded ADDITIONAL MATERIALS
21 st Century Math Projects
 * +, -. + / 0 1. 2 3 4 5 3 6 7 8 /! " # $ " % & ' ( )! ) If you are reading this, I ve likely become a Zombie. Do not trust that the rules of Zombieland will keep you safe. The Zombies have seen this film
* +, -. + / 0 1. 2 3 4 5 3 6 7 8 /! " # $ " % & ' ( )! ) If you are reading this, I ve likely become a Zombie. Do not trust that the rules of Zombieland will keep you safe. The Zombies have seen this film
8-1. The Pythagorean Theorem and Its Converse. Vocabulary. Review. Vocabulary Builder. Use Your Vocabulary
 8-1 The Pythagorean Theorem and Its Converse Vocabulary Review 1. Write the square and the positive square root of each number. Number 9 Square Positive Square Root 1 4 1 16 Vocabulary Builder leg (noun)
8-1 The Pythagorean Theorem and Its Converse Vocabulary Review 1. Write the square and the positive square root of each number. Number 9 Square Positive Square Root 1 4 1 16 Vocabulary Builder leg (noun)
Section 2C Formulas with Dividing Decimals
 Section 2C Formulas with Dividing Decimals x Look at the following z-score formula again from Statistics. z. Suppose we want to calculate the z-score if x 17.6 pounds, 13.8 pounds, and 2.5 pounds. Not
Section 2C Formulas with Dividing Decimals x Look at the following z-score formula again from Statistics. z. Suppose we want to calculate the z-score if x 17.6 pounds, 13.8 pounds, and 2.5 pounds. Not
Stats in Algebra, Oh My!
 Stats in Algebra, Oh My! The Curtis Center s Mathematics and Teaching Conference March 7, 2015 Kyle Atkin Kern High School District kyle_atkin@kernhigh.org Standards for Mathematical Practice 1. Make sense
Stats in Algebra, Oh My! The Curtis Center s Mathematics and Teaching Conference March 7, 2015 Kyle Atkin Kern High School District kyle_atkin@kernhigh.org Standards for Mathematical Practice 1. Make sense
The Bruins I.C.E. School
 The Bruins I.C.E. School Lesson 1: Decimal Place Value Lesson 2: Measurement and Data Lesson 3: Coordinate Graphing Lesson 4: Adding and Subtracting Fractions Lesson 5: Order of Operations Worksheets Included:
The Bruins I.C.E. School Lesson 1: Decimal Place Value Lesson 2: Measurement and Data Lesson 3: Coordinate Graphing Lesson 4: Adding and Subtracting Fractions Lesson 5: Order of Operations Worksheets Included:
Math 1070 Sample Final Exam Spring 2016
 University of Connecticut Department of Mathematics Spring 2016 Name: Instructor Name: Section: Read This First! This is a closed notes, closed book exam. You cannot receive aid on this exam from anyone
University of Connecticut Department of Mathematics Spring 2016 Name: Instructor Name: Section: Read This First! This is a closed notes, closed book exam. You cannot receive aid on this exam from anyone
4-3 Rate of Change and Slope. Warm Up. 1. Find the x- and y-intercepts of 2x 5y = 20. Describe the correlation shown by the scatter plot. 2.
 Warm Up 1. Find the x- and y-intercepts of 2x 5y = 20. Describe the correlation shown by the scatter plot. 2. Objectives Find rates of change and slopes. Relate a constant rate of change to the slope of
Warm Up 1. Find the x- and y-intercepts of 2x 5y = 20. Describe the correlation shown by the scatter plot. 2. Objectives Find rates of change and slopes. Relate a constant rate of change to the slope of
Bishop Kelley High School Summer Math Program Course: Trigonometry and Trigonometry with Pre-Calculus
 015 01 Summer Math Program Course: Trigonometr and Trigonometr with Pre-Calculus NAME: DIRECTIONS: Show all work on loose-leaf paper, which ou will turn in with the packet. (NO WORK IN PACKET!) Put final
015 01 Summer Math Program Course: Trigonometr and Trigonometr with Pre-Calculus NAME: DIRECTIONS: Show all work on loose-leaf paper, which ou will turn in with the packet. (NO WORK IN PACKET!) Put final
Week of July 2 nd - July 6 th. The denominator is 0. Friday
 Week of July 2 nd - July 6 th The temperature is F at 7 A.M. During the next three hours, the temperature increases 1 F. What is the temperature at 10 A.M.? A quotient is undefined. What does this mean?
Week of July 2 nd - July 6 th The temperature is F at 7 A.M. During the next three hours, the temperature increases 1 F. What is the temperature at 10 A.M.? A quotient is undefined. What does this mean?
Conversion: Feet, Metres, Paces, Chains
 Conversion: Feet, Metres, Paces, Chains Example: 1 inch = 2.54 cm 1. In our examples: 1 inch = 2.54 cm. To use algebra to find how many inches are in 140 cm: 1. Write the equivalency ratio 2. Write each
Conversion: Feet, Metres, Paces, Chains Example: 1 inch = 2.54 cm 1. In our examples: 1 inch = 2.54 cm. To use algebra to find how many inches are in 140 cm: 1. Write the equivalency ratio 2. Write each
Math Date Lesson Independent Work Computer Tuesday, Introduction (whole class) Critical Thinking Puzzles Count the Squares Math Riddles
 Introduction (whole class) Problem with Dice Critical Thinking Puzzles September 3 Station expectations Count the Squares Math Riddles Computer expectations (whole class) Tangrams Read permission slip
Introduction (whole class) Problem with Dice Critical Thinking Puzzles September 3 Station expectations Count the Squares Math Riddles Computer expectations (whole class) Tangrams Read permission slip
PATTERNS & FUNCTIONS
 PATTERNS & FUNCTIONS University of Houston Central Campus September 23, 2006 1 Warm-up Activity Test your knowledge by answering the following questions. No calculations or finger counting allowed. Good
PATTERNS & FUNCTIONS University of Houston Central Campus September 23, 2006 1 Warm-up Activity Test your knowledge by answering the following questions. No calculations or finger counting allowed. Good
8-1. The Pythagorean Theorem and Its Converse. Vocabulary. Review. Vocabulary Builder. Use Your Vocabulary
 8-1 he Pythagorean heorem and Its Converse Vocabulary Review 1. Write the square and the positive square root of each number. Number Square Positive Square Root 9 81 3 1 4 1 16 1 2 Vocabulary Builder leg
8-1 he Pythagorean heorem and Its Converse Vocabulary Review 1. Write the square and the positive square root of each number. Number Square Positive Square Root 9 81 3 1 4 1 16 1 2 Vocabulary Builder leg
Tying Knots. Approximate time: 1-2 days depending on time spent on calculator instructions.
 Tying Knots Objective: Students will find a linear model to fit data. Students will compare and interpret different slopes and intercepts in a context. Students will discuss domain and range: as discrete
Tying Knots Objective: Students will find a linear model to fit data. Students will compare and interpret different slopes and intercepts in a context. Students will discuss domain and range: as discrete
a fraction rock star in no time! This is a free calculator for adding, subtracting, multiplying, and dividing two fractions and/or mixed numbers.
 Fraction calculator The longest markings will be the quarter inch markings, ie. the first marking is 1/4 inch, the second is 1/2 (2/4) inch, the third is 3/4 inch. Calculate 3/4 by long division of 3 divided
Fraction calculator The longest markings will be the quarter inch markings, ie. the first marking is 1/4 inch, the second is 1/2 (2/4) inch, the third is 3/4 inch. Calculate 3/4 by long division of 3 divided
Common Core State Standards
 0 03 Pacing Guide for Sixth Grade Common Core State Standards Math Content Standards Ratios and Proportional Relationships RP Understand ratio concepts and use ratio reasoning to solve problems. The Number
0 03 Pacing Guide for Sixth Grade Common Core State Standards Math Content Standards Ratios and Proportional Relationships RP Understand ratio concepts and use ratio reasoning to solve problems. The Number
Name: Date: Math in Basketball: Take the Challenge Student Handout
 Name: Date: Math in Basketball: Take the Challenge Student Handout When NBA player Elton Brand steps to the free throw line, a number of key variables can influence his shot. Your challenge is to use the
Name: Date: Math in Basketball: Take the Challenge Student Handout When NBA player Elton Brand steps to the free throw line, a number of key variables can influence his shot. Your challenge is to use the
Unit 6, Lesson 1: Organizing Data
 Unit 6, Lesson 1: Organizing Data 1. Here is data on the number of cases of whooping cough from 1939 to 1955. a. Make a new table that orders the data by year. year number of cases 1941 222,202 1950 120,718
Unit 6, Lesson 1: Organizing Data 1. Here is data on the number of cases of whooping cough from 1939 to 1955. a. Make a new table that orders the data by year. year number of cases 1941 222,202 1950 120,718
Pacific Charter Institute Pacing Guide Grade(s): _5 Subject Area: _Math in Focus grade 5 CP: yes _X no
 Week 1 Pre-requisite skills review Chapter 1 pre-test Assessment 5 chapter pre-test pp. 1-4 or MIF Student book 5A pp. 1-4 Reteach 4A (1.1, 1.2, 2.1, 3.2, 3.4) NWEA Kids start Wed. Week 2 1.1 Writing numbers
Week 1 Pre-requisite skills review Chapter 1 pre-test Assessment 5 chapter pre-test pp. 1-4 or MIF Student book 5A pp. 1-4 Reteach 4A (1.1, 1.2, 2.1, 3.2, 3.4) NWEA Kids start Wed. Week 2 1.1 Writing numbers
RATES AND RATIOS WITH COMPLEX FRACTIONS. Complex Fractions. Fraction in the denominator
 RATES AND RATIOS WITH COMPLEX FRACTIONS LESSON.6 A complex fraction is a fraction that contains a fractional expression in its numerator, denominator or both. The following are examples of complex fractions.
RATES AND RATIOS WITH COMPLEX FRACTIONS LESSON.6 A complex fraction is a fraction that contains a fractional expression in its numerator, denominator or both. The following are examples of complex fractions.
A Study of Olympic Winning Times
 Connecting Algebra 1 to Advanced Placement* Mathematics A Resource and Strategy Guide Updated: 05/15/ A Study of Olympic Winning Times Objective: Students will graph data, determine a line that models
Connecting Algebra 1 to Advanced Placement* Mathematics A Resource and Strategy Guide Updated: 05/15/ A Study of Olympic Winning Times Objective: Students will graph data, determine a line that models
CCM8 Unit 7: Pythagorean Theorem Vocabulary
 CCM8 Unit 7: Pythagorean Theorem Vocabulary Base Exponent Hypotenuse Legs Perfect Square Pythagorean Theorem When a number is raised to a power, the number that is used as a factor The number that indicates
CCM8 Unit 7: Pythagorean Theorem Vocabulary Base Exponent Hypotenuse Legs Perfect Square Pythagorean Theorem When a number is raised to a power, the number that is used as a factor The number that indicates
Reliability. Introduction, 163 Quantifying Reliability, 163. Finding the Probability of Functioning When Activated, 163
 ste41912_ch04_123-175 3:16:06 01.29pm Page 163 SUPPLEMENT TO CHAPTER 4 Reliability LEARNING OBJECTIVES SUPPLEMENT OUTLINE After completing this supplement, you should be able to: 1 Define reliability.
ste41912_ch04_123-175 3:16:06 01.29pm Page 163 SUPPLEMENT TO CHAPTER 4 Reliability LEARNING OBJECTIVES SUPPLEMENT OUTLINE After completing this supplement, you should be able to: 1 Define reliability.
THE BEHAVIOR OF GASES
 14 THE BEHAVIOR OF GASES SECTION 14.1 PROPERTIES OF GASES (pages 413 417) This section uses kinetic theory to explain the properties of gases. This section also explains how gas pressure is affected by
14 THE BEHAVIOR OF GASES SECTION 14.1 PROPERTIES OF GASES (pages 413 417) This section uses kinetic theory to explain the properties of gases. This section also explains how gas pressure is affected by
of 6. Module 5 Ratios, Rates, & Proportions Section 5.1: Ratios and Rates MAT001 MODULE 5 RATIOS, RATES, & PROPORTIONS.
 Module 5 Ratios, Rates, & Proportions Section 5.1: Ratios and Rates A ratio is the comparison of two quantities that have the same units. 18 6 We can express this ratio three different ways: 18 to 6 18:6
Module 5 Ratios, Rates, & Proportions Section 5.1: Ratios and Rates A ratio is the comparison of two quantities that have the same units. 18 6 We can express this ratio three different ways: 18 to 6 18:6
GCSE Mathematics Practice Tests: Set 5
 GCSE Mathematics Practice Tests: Set 5 Paper 2H (Calculator) Time: 1 hour 30 minutes You should have: Ruler graduated in centimetres and millimetres, protractor, pair of compasses, pen, HB pencil, eraser,
GCSE Mathematics Practice Tests: Set 5 Paper 2H (Calculator) Time: 1 hour 30 minutes You should have: Ruler graduated in centimetres and millimetres, protractor, pair of compasses, pen, HB pencil, eraser,
MATH 110 Sample 02 Exam 1
 1. Evaluate: log 4 64 [A] 3 [B] 1 12 [C] 12 [D] 1 3 2. Given log 5 = T and log 2 = U, find log. [A] T + U [B] TU [C] T + U [D] TU. 3. Find x if e x 52 8 =, and ou are given ln 8 = 2.0794. [A] 0.3999 [B]
1. Evaluate: log 4 64 [A] 3 [B] 1 12 [C] 12 [D] 1 3 2. Given log 5 = T and log 2 = U, find log. [A] T + U [B] TU [C] T + U [D] TU. 3. Find x if e x 52 8 =, and ou are given ln 8 = 2.0794. [A] 0.3999 [B]
save percentages? (Name) (University)
 1 IB Maths Essay: What is the correlation between the height of football players and their save percentages? (Name) (University) Table of Contents Raw Data for Analysis...3 Table 1: Raw Data...3 Rationale
1 IB Maths Essay: What is the correlation between the height of football players and their save percentages? (Name) (University) Table of Contents Raw Data for Analysis...3 Table 1: Raw Data...3 Rationale
Mathematics (Project Maths Phase 3)
 *B6* Pre-Leaving Certificate Examination, 2014 Triailscrúdú na hardteistiméireachta, 2014 Mathematics (Project Maths Phase 3) Paper 1 Ordinary Level 2½ hours 300 marks Name: School: Address: Class: Teacher:
*B6* Pre-Leaving Certificate Examination, 2014 Triailscrúdú na hardteistiméireachta, 2014 Mathematics (Project Maths Phase 3) Paper 1 Ordinary Level 2½ hours 300 marks Name: School: Address: Class: Teacher:
Algebra 3.5 day 1.notebook. September 10, Bellwork
 Bellwork 1 Go over Quiz 2 Partners 3 Before we have our HW quiz, check your work and answers with last night's HW with your partner. If there is something your partner is not sure about, help them. If
Bellwork 1 Go over Quiz 2 Partners 3 Before we have our HW quiz, check your work and answers with last night's HW with your partner. If there is something your partner is not sure about, help them. If
When comparing two real gases at the same conditions, the one with the smaller particles is more ideal.
 Gas BASICS Gases are the most fun phases because mostly they are invisible and you have to use your measuring and wits to grasp how perfect they are. You already know that gases follow the Kinetic Molecular
Gas BASICS Gases are the most fun phases because mostly they are invisible and you have to use your measuring and wits to grasp how perfect they are. You already know that gases follow the Kinetic Molecular
Opleiding Informatica
 Opleiding Informatica Determining Good Tactics for a Football Game using Raw Positional Data Davey Verhoef Supervisors: Arno Knobbe Rens Meerhoff BACHELOR THESIS Leiden Institute of Advanced Computer Science
Opleiding Informatica Determining Good Tactics for a Football Game using Raw Positional Data Davey Verhoef Supervisors: Arno Knobbe Rens Meerhoff BACHELOR THESIS Leiden Institute of Advanced Computer Science
Bellwork MCT Practice Test (Form A) Problem numbers.
 Course 7 th Grade Math Student Objective (Obj. 5d) TSW determine probability through experimentation and calculations. DETAIL LESSON PLAN Tuesday, April 16 / Wednesday, April 17 Lesson 12-1, 12-2 Probability
Course 7 th Grade Math Student Objective (Obj. 5d) TSW determine probability through experimentation and calculations. DETAIL LESSON PLAN Tuesday, April 16 / Wednesday, April 17 Lesson 12-1, 12-2 Probability
Summer Work. 6 th Grade Enriched Math to 7 th Grade Pre-Algebra
 Summer Work 6 th Grade Enriched Math to 7 th Grade Pre-Algebra Attached is a packet for Summer 2017. Take your time. Do not wait until the weeks right before school to begin. The benefit of summer work
Summer Work 6 th Grade Enriched Math to 7 th Grade Pre-Algebra Attached is a packet for Summer 2017. Take your time. Do not wait until the weeks right before school to begin. The benefit of summer work
Week 1, Lesson 2 1. Warm up 2. Notes Quadratics 3. ICA Physics Rocket
 Do all functions follow patterns? Essential Question Essential Question Essential Question Essential Question Essential Question Essential Question Essential Question Week 1, Lesson 2 1. Warm up 2. Notes
Do all functions follow patterns? Essential Question Essential Question Essential Question Essential Question Essential Question Essential Question Essential Question Week 1, Lesson 2 1. Warm up 2. Notes
CONTENTS III CUMULATIVE REVIEW Copyright by Phoenix Learning Resources. Inc. All Rights Reserved.
 CONTENTS Chapter 1 WHOLE NUMBERS Pretest.............................. 1 Adding Whole Numbers.................. 2 Subtracting Whole Numbers.............. 4 Adding and Subtracting Whole Numbers..... 7 Using
CONTENTS Chapter 1 WHOLE NUMBERS Pretest.............................. 1 Adding Whole Numbers.................. 2 Subtracting Whole Numbers.............. 4 Adding and Subtracting Whole Numbers..... 7 Using
3. Answer the following questions with your group. How high do you think he was at the top of the stairs? How did you estimate that elevation?
 J Hart Interactive Algebra 1 Classwork Exploratory Challenge 1. Watch the first 1:08 minutes of the video below and describe in words the motion of the man. Elevation vs. Time #2 [http://www.mrmeyer.com/graphingstories1/graphingstories2.mov.
J Hart Interactive Algebra 1 Classwork Exploratory Challenge 1. Watch the first 1:08 minutes of the video below and describe in words the motion of the man. Elevation vs. Time #2 [http://www.mrmeyer.com/graphingstories1/graphingstories2.mov.
Chapter 0 Pretest = 4
 Determine whether you need an estimate or an exact answer. Then solve. 1. SHOPPING Addison paid $1.29 for gum and $0.89 for a package of notebook paper. She gave the cashier a $5 bill. If the tax was $0.14,
Determine whether you need an estimate or an exact answer. Then solve. 1. SHOPPING Addison paid $1.29 for gum and $0.89 for a package of notebook paper. She gave the cashier a $5 bill. If the tax was $0.14,
Class VII EXAM TYPE & SUBJECT. English PERIODIC TEST 1 ( ) Bengali PERIODIC TEST 1
 Class VII SUBJECT English PERIODIC TEST 1 (18.06.18 25.06.18) (03.09.18 10.09.18) (23.11.18 06.12.18) ORC : My Big Brother, Leisure RAPID READER : Chapter 1, 2, 3 GRAMMAR : Tenses, Preposition WRITING
Class VII SUBJECT English PERIODIC TEST 1 (18.06.18 25.06.18) (03.09.18 10.09.18) (23.11.18 06.12.18) ORC : My Big Brother, Leisure RAPID READER : Chapter 1, 2, 3 GRAMMAR : Tenses, Preposition WRITING
June x. 2. x. 3. x. Sunday Monday Tuesday Wednesday Thursday Friday Saturday 8.NS.1 8.NS.1 8.NS.1 8.NS.1 8.NS /3 + 1/9 2.
 June 2018 Sunday Monday Tuesday Wednesday Thursday Friday Saturday 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 Father s Day 24 25 26 27 28 29 30 1. 1/3 + 1/9 2. 1 8/9 + 3 2/3 3. 9 6/7 +
June 2018 Sunday Monday Tuesday Wednesday Thursday Friday Saturday 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 Father s Day 24 25 26 27 28 29 30 1. 1/3 + 1/9 2. 1 8/9 + 3 2/3 3. 9 6/7 +
AP Physics 1 Summer Packet Review of Trigonometry used in Physics
 AP Physics 1 Summer Packet Review of Trigonometry used in Physics For some of you this material will seem pretty familiar and you will complete it quickly. For others, you may not have had much or any
AP Physics 1 Summer Packet Review of Trigonometry used in Physics For some of you this material will seem pretty familiar and you will complete it quickly. For others, you may not have had much or any
2012 P.A.P.A-2 FREE-RESPONSE QUESTIONS (Calc OK)
 1 P.A.P.A- FREE-RESPONSE QUESTIONS (Calc OK) 1) At the Jackson County Fair held each October, there are many games and attractions which launch things into the air. One game is a football toss where the
1 P.A.P.A- FREE-RESPONSE QUESTIONS (Calc OK) 1) At the Jackson County Fair held each October, there are many games and attractions which launch things into the air. One game is a football toss where the
Below are the graphing equivalents of the above constraints.
 Detailed Step- by- Step description of the Wilson Problem Part A. LP Formulation Step 1. Figure out the problem Although it may seem obvious, the first step in solving the Wilson Problem is to understand
Detailed Step- by- Step description of the Wilson Problem Part A. LP Formulation Step 1. Figure out the problem Although it may seem obvious, the first step in solving the Wilson Problem is to understand
Chapter 7: Quadratics
 Chapter 7: Quadratics Notes 7.8 Quadratic Modeling Name: Set up a quadratic equation to model the scenario and use ANY method to solve: Vertex Form to find max/min or symmetry Factoring to find zeros/solutions
Chapter 7: Quadratics Notes 7.8 Quadratic Modeling Name: Set up a quadratic equation to model the scenario and use ANY method to solve: Vertex Form to find max/min or symmetry Factoring to find zeros/solutions
Black Sea Bass Encounter
 Black Sea Bass Encounter Below is an adaptation of the Shark Encounter (Lawrence Hall of Science: MARE 2002) lesson plan to be about Black Sea Bass and to incorporate information learned from Dr. Jensen
Black Sea Bass Encounter Below is an adaptation of the Shark Encounter (Lawrence Hall of Science: MARE 2002) lesson plan to be about Black Sea Bass and to incorporate information learned from Dr. Jensen
LEVEL 2 FUNCTIONAL SKILLS MATHEMATICS 09866
 OXFORD CAMBRIDGE AND RSA EXAMINATIONS LEVEL 2 FUNCTIONAL SKILLS MATHEMATICS 09866 TASK AND ANSWER BOOKLET PRACTICE PAPER 2 INSTRUCTIONS TIME: 1 HOUR 30 MINUTES Fill in all the boxes below. Make sure your
OXFORD CAMBRIDGE AND RSA EXAMINATIONS LEVEL 2 FUNCTIONAL SKILLS MATHEMATICS 09866 TASK AND ANSWER BOOKLET PRACTICE PAPER 2 INSTRUCTIONS TIME: 1 HOUR 30 MINUTES Fill in all the boxes below. Make sure your
Unit 2 Day 4 Notes Law of Sines
 AFM Unit 2 Day 4 Notes Law of Sines Name Date Introduction: When you see the triangle below on the left and someone asks you to find the value of x, you immediately know how to proceed. You call upon your
AFM Unit 2 Day 4 Notes Law of Sines Name Date Introduction: When you see the triangle below on the left and someone asks you to find the value of x, you immediately know how to proceed. You call upon your
Accuplacer Arithmetic Study Guide
 Accuplacer Arithmetic Study Guide Section One: Terms Numerator: The number on top of a fraction which tells how many parts you have. Denominator: The number on the bottom of a fraction which tells how
Accuplacer Arithmetic Study Guide Section One: Terms Numerator: The number on top of a fraction which tells how many parts you have. Denominator: The number on the bottom of a fraction which tells how
MORE TRIGONOMETRY
 MORE TRIGONOMETRY 5.1.1 5.1.3 We net introduce two more trigonometric ratios: sine and cosine. Both of them are used with acute angles of right triangles, just as the tangent ratio is. Using the diagram
MORE TRIGONOMETRY 5.1.1 5.1.3 We net introduce two more trigonometric ratios: sine and cosine. Both of them are used with acute angles of right triangles, just as the tangent ratio is. Using the diagram
Lesson 22: Getting the Job Done Speed, Work, and Measurement Units
 Lesson 22: Getting the Job Done Speed, Work, and Measurement Units Student Outcomes Students decontextualize a given speed situation, representing symbolically the quantities involved with the formula.
Lesson 22: Getting the Job Done Speed, Work, and Measurement Units Student Outcomes Students decontextualize a given speed situation, representing symbolically the quantities involved with the formula.
STRATEGIES ACHIEVE MATHEMATICS SUCCESS
 STAMS SERIES D STRATEGIES TO ACHIEVE MATHEMATICS SUCCESS PROVIDES INSTRUCTIONAL ACTIVITIES FOR 12 MATHEMATICS STRATEGIES USES A STEP-BY-STEP APPROACH TO ACHIEVE MATHEMATICS SUCCESS PREPARES STUDENTS FOR
STAMS SERIES D STRATEGIES TO ACHIEVE MATHEMATICS SUCCESS PROVIDES INSTRUCTIONAL ACTIVITIES FOR 12 MATHEMATICS STRATEGIES USES A STEP-BY-STEP APPROACH TO ACHIEVE MATHEMATICS SUCCESS PREPARES STUDENTS FOR
Note! In this lab when you measure, round all measurements to the nearest meter!
 Distance and Displacement Lab Note! In this lab when you measure, round all measurements to the nearest meter! 1. Place a piece of tape where you will begin your walk outside. This tape marks the origin.
Distance and Displacement Lab Note! In this lab when you measure, round all measurements to the nearest meter! 1. Place a piece of tape where you will begin your walk outside. This tape marks the origin.
Lesson 1: Decimal Place Value. Concept/Topic to Teach: Students use Bruins statistical data to order and compare decimals to the thousandths.
 Math Lesson 1: Decimal Place Value Concept/Topic to Teach: Students use Bruins statistical data to order and compare decimals to the thousandths. Standards Addressed: Standard 1: 5.NBT.3 Read, write, and
Math Lesson 1: Decimal Place Value Concept/Topic to Teach: Students use Bruins statistical data to order and compare decimals to the thousandths. Standards Addressed: Standard 1: 5.NBT.3 Read, write, and
Dino's Decimal Division
 Dino's Decimal Division Miss Sullivan designed a new game called Dino s Decimal Division. The game begins when a player chooses two numbers from a hat. The player divides the two numbers. If the numbers
Dino's Decimal Division Miss Sullivan designed a new game called Dino s Decimal Division. The game begins when a player chooses two numbers from a hat. The player divides the two numbers. If the numbers
