-tr~::!)::~ == ~~i~5".;j ~-~~--:H-r~-J
|
|
|
- Cecil Flynn
- 6 years ago
- Views:
Transcription
1 R.Katiraie MA103 Quiz 2 Sections (1.6, 1.7, 2.1, 2.2) Name.----f'&---'-'O--( -~Solve the equation. 1) 5x~ (4x - 1) = 2 ~_~_. 5)(- tf..t +' :=. X --r I -=?. (... G:~i:) 2) -6x + 7{2x - 3) = -5-8x -~~+\4-)( -~\ ::: -5 - <6X ~)l-.37 [:= '1.1 -=- -S"- 'it I] \~~ -1.\.=- - 5" ~ /t X - 1 Solve for the specified letter. 1 3) V =3"Bh, for h 4) Bill swims at a speed of 6.6 mph in still water. The river he's in flows at a speed of 5.7 mph. How long will it take Bill to swim 1.1 mi upstream? Round your answer to the nearest tenth of an hour, if necessary. -tr~::!)::~ == ~~i~5".;j ~-~~--:H-r~-J x-7 5) Find f(2) when f(x) = 5x ) Find g{a)- 1 when g{x) = 5x - 2. (please Simplify your answer) '-v A-I
2 7) Find g(a - 1) when g(x) =5x - 4. (Please simplify your answer) 8) The function h described by h(t):; -16t t gives the height of a ball thrown upward with a speed of 33.1 feet per second from a ft high window t seconds after it is thrown until it hits the ground. Find the height of the ball 1.8 seconds after it is thrown. ;:w = ~ ~~, ~").) ()~~... ~(,:.;.~) Find the rate of change. Use appropriate units. 9) ( C3.i ~ 80 y (S" 'L.y Afj R.dJ.. -ft~.~ = ~3 - Q Distance 40 5""- C) Traveled 30 in Miles "",..._ x Number of Hours Spent Traveling 10) A deep sea diving bell is being lowered at a constant rate. After 8 minutes, the bell is at a depth of 400 feet. After 45 minutes the bell is at a depth of 1300 feet. What is the average rate of lowering per minute? - ::: 2 if.]?-!~ tvl'~ A-2
3 / fuaie MA103 Quiz 2 Sections (1.6, 1.7,2.1,2.2) e._ e_o\_~_ _:S_ C;;olve for the specified letter. 1 1) V =-Bh, forh 3 Solve the equation. 2) 9x + 4(-2x - 3) = -2-9x?K-'6'J..-\'2- = -'t-9x 'I..- -\1... =. -1,-~i... ~j1~~~..._..~~,~:::~._±",9,~.. 3) 6x - (3x - 1) = 2 t ')(_3 ~ + \.:=' 'L '3 'I- k\ ::; 1. \t))(='~ =) \1-=1) 4) Find g(a - 1) when g(x) = 5x - 2. (Please simplify your answer) := S""Q..- s-'l ~:~7J 5) Find g(a}+ 1 when g(x) = 5x + 4. (Please simplify your answer) x-4 6) Find (-4) when f(x) =--. 6x ~ ~(_~:= -4--lf... ~ _.~ --~ ~(-V+'1-1-it1 -'7 J7 B-1
4 / fuaie MAI03 Quiz 2 Sections (1.6, 1.7,2.1,2,2) j?'o\~5 ~olve for the specified letter. 1) V = "3 1 Bh, forh 3V == Bh Solve the equation. 2) 9x + 4(-2x - 3) = -2-9x ~X-<6'J.--\'2. = -'L-9X 'I..- -\1... =. -?--~y... ~~,_. ~ ~"~..." ~'::~--,±:,9,~ 3) 6x - (3x - 1) = 2 ~ ')( _ 3 ~ + \.::;:;' 1., \t;))(=\~ =3 \~=\) '3 '" k ~ ::; 1. 4) Find g(a - 1) when g(x) = 5x - 2. (Please simplify your answer) 'a(a.-0 :-$( 'to := '-1.= 5et ':"'J '-'''''''I'II/IIloIl:llIU\~~'-'- 5) Find g(a)+ 1 when g(x) = 5x + 4. (Please simplify your answer) x-4 6) Find (-4) when f(x) = 6x + 7' _., " ==- -- ~(-L\;):= -4--Lf - ~ ~(-V+"1-1.'1+1 -,7 If B-1
5 the rate of Change~riateunits) 7) o~ ) C,.J~) 80 Y Distance 40 Traveled 30 in Miles 20 ( "f/~j.) 2. ~ x... Number of Hours Spent Traveling 8) A deep sea diving bell is being lowered at a constant rate. After 8 minutes, the bell is at a depth of 500 feet. (~. After 55 minutes the.bell is at a depth of 1800 feet. What is the average rate of low~tm~~ik;:.rsl'ov) C'S!J I'iQ~ ~«'d:l.=: as OQ~-- 5~ ~.11r~1'e1:t_tr\ ~] 9) Bill swims at a speed of 6.7 mph in Still water. The river h~s m:1i~ws at a speed of 2.1 mph. How long will it take Bill to swim 1.7 mi upstream? Round your answer t? the nearest tenth of an hour, if necessary. ~ t,~::=--d-.s+~c.sl ::: I 7 = (). 3'/ HP-.. JfJ2e J ~~( -'1.-.P ~~.lf It~.. 10) The function h described by h(t) =-16t lt gives the height of a ball thrown upward with a speed of 33.1 feet per second from a ft high window t seconds after it is thrown until it hits the ground. Find the height of the ball 1.2 seconds after it is thrown. hel.1-).::: -\t,( \.1.) \ (Q)+\ 2J f 'L( :==-llfo.11- ~~
6 ~tiraie MA103 Quiz 2 Sections (1.6, 1.7, 2.1, 2.2) Name ~\~~ l, _ --Solve the equation. ~ 1) 5x - (4x - 1) =2 2) -6x + 7(2x - 3) = -5-8x s- X-- t )(+\ ;:;. "L ~ +\ :;; 1.. -l -~ -b ~ -+ \'f ~-1..\.; --s - B~ tt ~". _ 'tt ::"~ -- ~ -.8)( ""~-.-. ';-,~-\)""". Solvo for tho ~~!;.Od lo:r. \ (" :: ) V = 3"Bh, for h.~ 4) Bill swims at a speed of 6.6 mph in still water. The river he's in flows at a speed of 5.7 mph. How long will it \ take Bill to swim 1.1 mi upstream? Round your answer to the nearest tenth of an hour, if necessary. t.tf~ ~. x-7 5) Find f(2) when f(x) = 5x _-_._J_. ~((A)-\ :' 5"G-.-J ' 6) Find g(a)- 1 when g(x) =5x - 2. (please simplify your answer).._.,_.,...~~~~---, C-I
7 g(a-l) wheng(x)=5x-4. (please simplify your answer) 8) The function h described byh(t) =-16t t gives the height of a ball thrown upward with a speed of 33.1 feet per second from a t high window t seconds after it is thrown until it hits the ground. Find the height ofthe ball 1.8 seconds after it is thrown. h("~:: _.\l(\,~)~~,1~\,( \-i)+\ tt. tf~ 2 b Find the rate of change. Use appropriate units. 9) (0)0) Distance 40 Traveled 30 in Miles Y ~~t) -- --' 7-2-0' S"-Q x Number of Hours Spent Traveling 10) A deep sea diving bell is being lowered at a constant rate. After8 minutes, the bell is at a depth of 400 feet. After 45 minutes the bell is at a depth of 1300 feet. What is the average rate of lowering per minute? ~~'t-- fj\) (~~ (~. \1~ '~~~~~H=~~ O\)_.. ;=. 2if. 32, if~-, ~' ~ c-~
8 , L.!aie MA103 SO\~ I-~- Quiz 2 Sections (1.6, 1.7,2.1,2.2) ~olve the equation. 1) 7x-(3x-1)~2 2) -8x + 4(-3x - 4) = -31-5x 4) A deep sea diving bell is being lowered at a constant rate. After 10 minutes, the bell is at a depth of 600 feet. ~ After 50 minutes the bell is at a depth of 2000 feet. What is the average rate of lowering per minute? Vl\~~. ~~:t I ( \0 kt)oj Vt~ :: '2 ~ - ~q~, (cf\:),~ "'- ~ ~.._-" ~~ 'lociivj 11, ) ~ ~(lit:~~~~~~.!il~ ~~ «O~~ J.f ~) 2.0«> ~~ $"";"-I~ f'<> 4 5) Bill swims at a speed of 4.9 mph in still water. The river he's in flows at a speed of -2.7 mph. How long will it take Bill to swim 2.8 mi upstream? Round your answer to the nearest tenth of an hour, if necessary. _ , ("f\l \.A!<,,,,! D_1
9 8) The function h described byh(t) =0-16t t gives the height of a ball thrown upward with a speed of 33.1 feet per second from a ft high window t seconds after it is thrown until it hits the ground. Find the height of the ball 1.1 seconds after it is thrown. hci;() ~_,';~( \.\)fi~~,~1~\\( rjj ~ ::: Jl{f:iT""f:J'J llind the rate of change. Use appropriate units. ~ 9) 80 y Distance 40 Traveled 30 in Miles x Number of Hours Spent Traveling 10) Find g(a)- 1 when g(x) =0 5x - 5. (Please simplify your answer) _... sn I ~"""""'.."='"" "~c,~~.' '._"]'"' ",~, -.,,, V'\. -~, indgi!0qlli_ D_2
Math 081 Worksheet Section 8.4 v01 Spring 2011 Dressler. Name. 6) 12 dm. Find the area of the geometric figure. 1) 5 m. Rectangle. 25.
 Math 081 Worksheet Section 8.4 v01 Spring 2011 Dressler Name 6) 12 dm Find the area of the geometric figure. 1) 5 dm Rectangle 5 m ) 6.8 m 12 units 25.5 units 2) 22.5 units Rectangle 3 m 8).9 m 20 yd 52
Math 081 Worksheet Section 8.4 v01 Spring 2011 Dressler Name 6) 12 dm Find the area of the geometric figure. 1) 5 dm Rectangle 5 m ) 6.8 m 12 units 25.5 units 2) 22.5 units Rectangle 3 m 8).9 m 20 yd 52
i6c*mzr \O+hf tlnu s\ock-
 i6c*mzr \O+hf tlnu s\ock- L Quadratic Racl't cz ae! #- Formula Word Problems Name: Period: 1. Jason jumped off of a cliff into the ocean in Acapulco while vacationing with some friends. His height as a
i6c*mzr \O+hf tlnu s\ock- L Quadratic Racl't cz ae! #- Formula Word Problems Name: Period: 1. Jason jumped off of a cliff into the ocean in Acapulco while vacationing with some friends. His height as a
Name: Date: Math in Basketball: Take the Challenge Student Handout
 Name: Date: Math in Basketball: Take the Challenge Student Handout When NBA player Elton Brand steps to the free throw line, a number of key variables can influence his shot. Your challenge is to use the
Name: Date: Math in Basketball: Take the Challenge Student Handout When NBA player Elton Brand steps to the free throw line, a number of key variables can influence his shot. Your challenge is to use the
Quadratic Word Problems
 Quadratic Word Problems Normally, the graph is a maximum ( x 2 /opens down) because of the real life scenarios that create parabolas. The equation of the quadratic will be given. We will only be using
Quadratic Word Problems Normally, the graph is a maximum ( x 2 /opens down) because of the real life scenarios that create parabolas. The equation of the quadratic will be given. We will only be using
Mixed Trig Problems. For each problem show a complete solution with diagrams that include all the pertinent facts and answers.
 Mixed Trig Problems For each problem show a complete solution with diagrams that include all the pertinent facts In ABC, cos A = 0.6. Find sin A and tan A. In ABC, cos A = 0.6. Find sin A and tan A. Sin
Mixed Trig Problems For each problem show a complete solution with diagrams that include all the pertinent facts In ABC, cos A = 0.6. Find sin A and tan A. In ABC, cos A = 0.6. Find sin A and tan A. Sin
Motion Projectile Problems (MPP)
 Math 104 _ q2v0v1m6b `Kau`thaq ]SPoEfOtHwOaCrmeC rlsljc^.s f UAOlAlO NrUihgohatOst iree`see]rkveebdr. Motion Projectile Problems (MPP) 30102016 1) Erika jumped off a cliff into the ocean in Acapulco while
Math 104 _ q2v0v1m6b `Kau`thaq ]SPoEfOtHwOaCrmeC rlsljc^.s f UAOlAlO NrUihgohatOst iree`see]rkveebdr. Motion Projectile Problems (MPP) 30102016 1) Erika jumped off a cliff into the ocean in Acapulco while
1. Scuba diver a scuba diver dives straight down into the water quantities: the depth of the dive the water pressure on the diver
 HW - Functions and Rates name in #1-10, several situations are given below. for each, answer the following questions: a) does one quantity depend on another? if so, how? b) if the answer to (a) is yes,
HW - Functions and Rates name in #1-10, several situations are given below. for each, answer the following questions: a) does one quantity depend on another? if so, how? b) if the answer to (a) is yes,
TOPIC III: Proportional Reasoning. Good Luck to:
 Good Luck to: Period: Date DIRECTIONS: Show all work in the space provided. 1. Joniqua wants to get an A in her Algebra 1 class. So far she has four test scores; 77%, 83%, 97%, and 95%. Which choice best
Good Luck to: Period: Date DIRECTIONS: Show all work in the space provided. 1. Joniqua wants to get an A in her Algebra 1 class. So far she has four test scores; 77%, 83%, 97%, and 95%. Which choice best
Design, Operation and Maintenance of a Swimming Pool
 Page 1 of 2 WASHINGTON STATE MATHEMATICS COUNCIL 2018 MIDDLE SCHOOL MATH OLYMPIAD Session I: PROBLEM SOLVING Design, Operation and Maintenance of a Swimming Pool The City is planning to build a swimming
Page 1 of 2 WASHINGTON STATE MATHEMATICS COUNCIL 2018 MIDDLE SCHOOL MATH OLYMPIAD Session I: PROBLEM SOLVING Design, Operation and Maintenance of a Swimming Pool The City is planning to build a swimming
REVIEW TEST Find the least common multiple (LCM) of the numbers 4, 18. A) 4 B) 2 C) 72 D) 1 E) 36
 REVIEW TEST 2. Find the least common multiple (LCM) of the numbers, 8. 2 72 6 2. Find the least common multiple (LCM) of the numbers 2, 20. 20 60 2. Find the greatest common factor (GCF) of the numbers,
REVIEW TEST 2. Find the least common multiple (LCM) of the numbers, 8. 2 72 6 2. Find the least common multiple (LCM) of the numbers 2, 20. 20 60 2. Find the greatest common factor (GCF) of the numbers,
KINETICS Seismic Design Manual
 KCAB Wedge Type Anchor Selection Guide For wedge type concrete anchors, the factor of safety is computed using the following equation. F.S. 1 = 1/[(T/T A ) (5/3) + (P/P A ) (5/3) ] (Eq. P1.3.1-1) Where:
KCAB Wedge Type Anchor Selection Guide For wedge type concrete anchors, the factor of safety is computed using the following equation. F.S. 1 = 1/[(T/T A ) (5/3) + (P/P A ) (5/3) ] (Eq. P1.3.1-1) Where:
of 6. Module 5 Ratios, Rates, & Proportions Section 5.1: Ratios and Rates MAT001 MODULE 5 RATIOS, RATES, & PROPORTIONS.
 Module 5 Ratios, Rates, & Proportions Section 5.1: Ratios and Rates A ratio is the comparison of two quantities that have the same units. 18 6 We can express this ratio three different ways: 18 to 6 18:6
Module 5 Ratios, Rates, & Proportions Section 5.1: Ratios and Rates A ratio is the comparison of two quantities that have the same units. 18 6 We can express this ratio three different ways: 18 to 6 18:6
Transportation Costs (or Trucker s Dilemma) Math 1050 College Algebra Project
 Amanda Farris, Kristina Paff & Bradley Wagner MTWH 12-12:50 Transportation Costs (or Trucker s Dilemma) Math 1050 College Algebra Project A truck driving 260 miles over a flat interstate at a constant
Amanda Farris, Kristina Paff & Bradley Wagner MTWH 12-12:50 Transportation Costs (or Trucker s Dilemma) Math 1050 College Algebra Project A truck driving 260 miles over a flat interstate at a constant
Skills Practice Skills Practice for Lesson 3.1
 Skills Practice Skills Practice for Lesson.1 Name Date Get Radical or (Be) 2! Radicals and the Pythagorean Theorem Vocabulary Write the term that best completes each statement. 1. An expression that includes
Skills Practice Skills Practice for Lesson.1 Name Date Get Radical or (Be) 2! Radicals and the Pythagorean Theorem Vocabulary Write the term that best completes each statement. 1. An expression that includes
Math 15 Test 3 Review Section Change 4.5 yards to inches. Round your answer to the nearest inch. (1 yd = 3 ft, 1 ft = 12 in)
 Page 1 Math 15 Section 6.3 18. Change 4.5 yards to inches. Round your answer to the nearest inch. (1 yd = 3 ft, 1 ft = 12 in) 30. Change 528 inches to feet. (1 ft = 12 in) 42. Change 3 1/16 pounds to ounces.
Page 1 Math 15 Section 6.3 18. Change 4.5 yards to inches. Round your answer to the nearest inch. (1 yd = 3 ft, 1 ft = 12 in) 30. Change 528 inches to feet. (1 ft = 12 in) 42. Change 3 1/16 pounds to ounces.
Mathematics in Sports
 Mathematics in Sports Although not always realized, mathematics plays a very important role in sports. Whether discussing a players statistics, a coaches formula for drafting certain players, or even a
Mathematics in Sports Although not always realized, mathematics plays a very important role in sports. Whether discussing a players statistics, a coaches formula for drafting certain players, or even a
Physics 23 Exam 1 Spring 2009 Dr. Alward Page 1
 Physics 23 Exam 1 Spring 2009 Dr. Alward Page 1 1. An arrow is fired upward at a speed of 100 m/s. What will be its height (in meters) one second before it reaches its maximum height? A) 505 B) 496 C)
Physics 23 Exam 1 Spring 2009 Dr. Alward Page 1 1. An arrow is fired upward at a speed of 100 m/s. What will be its height (in meters) one second before it reaches its maximum height? A) 505 B) 496 C)
STAAR Practice Test #1. 2 (2B) What is the equation in standard form of the line that
 STAAR Practice Test #1 TEKS 2 (Linear Equations) 1. (2B) The population of Webb County, Texas, from the year 2000 through 2010 is shown in the graph. If the trend shown in the graph continues, what will
STAAR Practice Test #1 TEKS 2 (Linear Equations) 1. (2B) The population of Webb County, Texas, from the year 2000 through 2010 is shown in the graph. If the trend shown in the graph continues, what will
Pythagorean Theorem Review Missing Hypotenuse. Name: Mr. Fourmy.
 Name: Mr. Fourmy Date: Period: -------------------------- ---------------- Pythagorean Theorem Review Missing Hypotenuse --------- Directions: Using the Pythagorean Theorem.jind the missing side length/or
Name: Mr. Fourmy Date: Period: -------------------------- ---------------- Pythagorean Theorem Review Missing Hypotenuse --------- Directions: Using the Pythagorean Theorem.jind the missing side length/or
Simplifying Radical Expressions and the Distance Formula
 1 RD. Simplifying Radical Expressions and the Distance Formula In the previous section, we simplified some radical expressions by replacing radical signs with rational exponents, applying the rules of
1 RD. Simplifying Radical Expressions and the Distance Formula In the previous section, we simplified some radical expressions by replacing radical signs with rational exponents, applying the rules of
Bishop Kelley High School Summer Math Program Course: Trigonometry and Trigonometry with Pre-Calculus
 015 01 Summer Math Program Course: Trigonometr and Trigonometr with Pre-Calculus NAME: DIRECTIONS: Show all work on loose-leaf paper, which ou will turn in with the packet. (NO WORK IN PACKET!) Put final
015 01 Summer Math Program Course: Trigonometr and Trigonometr with Pre-Calculus NAME: DIRECTIONS: Show all work on loose-leaf paper, which ou will turn in with the packet. (NO WORK IN PACKET!) Put final
Warm up Warm up Warm up Warm up Warm up Warm up Warm up Warm up Warm up Warm up Warm up Warm up Warm up Warm up Warm up Warm up Warm up
 Solve applied problems using the attributes of similar triangles. Solve problems using ratio and proportions. Investigate the fundamental concepts behind trigonometry: three basic trig functions and how
Solve applied problems using the attributes of similar triangles. Solve problems using ratio and proportions. Investigate the fundamental concepts behind trigonometry: three basic trig functions and how
1. A right triangle has legs of 8 centimeters and 13 centimeters. Solve the triangle completely.
 9.7 Warmup 1. A right triangle has legs of 8 centimeters and 13 centimeters. Solve the triangle completely. 2. A right triangle has a leg length of 7 in. and a hypotenuse length of 14 in. Solve the triangle
9.7 Warmup 1. A right triangle has legs of 8 centimeters and 13 centimeters. Solve the triangle completely. 2. A right triangle has a leg length of 7 in. and a hypotenuse length of 14 in. Solve the triangle
Are We There Yet? IPv6 as Related to GDP per Capita. By Alain Durand November 28 th,` 2016
 Are We There Yet? as Related to By Alain Durand November 28 th,` 2016 Quesons for this Study: I. Where are we across the globe with adoption? a. Is deployed uniformly? b. Is there a rich country/poor country
Are We There Yet? as Related to By Alain Durand November 28 th,` 2016 Quesons for this Study: I. Where are we across the globe with adoption? a. Is deployed uniformly? b. Is there a rich country/poor country
USEFUL RELATIONSHIPS
 Use the chart below for the homework problems in this section. USEFUL RELATIONSHIPS U.S. Customary 12 in. = 1 ft 3 ft = 1 yd 280 ft = 1 mi 16 oz = 1 lb 2000 lbs = 1 T 8 fl oz = 1 c 2 c = 1 pt 2 pts = 1
Use the chart below for the homework problems in this section. USEFUL RELATIONSHIPS U.S. Customary 12 in. = 1 ft 3 ft = 1 yd 280 ft = 1 mi 16 oz = 1 lb 2000 lbs = 1 T 8 fl oz = 1 c 2 c = 1 pt 2 pts = 1
Design, Operation and Maintenance of a Swimming Pool
 Page 1 of 2 WASHINGTON STATE MATHEMATICS COUNCIL 2018 MIDDLE SCHOOL MATH OLYMPIAD Session I: PROBLEM SOLVING Design, Operation and Maintenance of a Swimming Pool The City is planning to build a swimming
Page 1 of 2 WASHINGTON STATE MATHEMATICS COUNCIL 2018 MIDDLE SCHOOL MATH OLYMPIAD Session I: PROBLEM SOLVING Design, Operation and Maintenance of a Swimming Pool The City is planning to build a swimming
RATE OF CHANGE AND INSTANTANEOUS VELOCITY
 RATE OF CHANGE AND INSTANTANEOUS VELOCITY Section 2.2A Calculus AP/Dual, Revised 2017 viet.dang@humbleisd.net 7/30/2018 1:34 AM 2.2A: Rates of Change 1 AVERAGE VELOCITY A. Rates of change play a role whenever
RATE OF CHANGE AND INSTANTANEOUS VELOCITY Section 2.2A Calculus AP/Dual, Revised 2017 viet.dang@humbleisd.net 7/30/2018 1:34 AM 2.2A: Rates of Change 1 AVERAGE VELOCITY A. Rates of change play a role whenever
CRS SKILL LEVEL DESCRIPTION Level 1 ALL students must R- NCP 505 Work with squares and square roots
 PPF 502 & PPF 504 Work Sheet Period Name CRS SKILL LEVEL DESCRIPTION Level 1 ALL students must R- NCP 505 Work with squares and square roots attain mastery at this level Level 2 MOST students will PPF
PPF 502 & PPF 504 Work Sheet Period Name CRS SKILL LEVEL DESCRIPTION Level 1 ALL students must R- NCP 505 Work with squares and square roots attain mastery at this level Level 2 MOST students will PPF
When it is 80 degrees he will sell about 42 ice creams.
 What are some of the ways Functions are represented? Essential Question Essential Question Essential Question Essential Question Essential Question Essential Question Essential Question Week 4, Lesson
What are some of the ways Functions are represented? Essential Question Essential Question Essential Question Essential Question Essential Question Essential Question Essential Question Week 4, Lesson
Exercise (3): Open Channel Flow Rapidly Varied Flow
 Exercise (3): Open Channel Flow Rapidly Varied Flow 1) A hydraulic jump exists in a trapezoidal channel having a bed width of 7 m and side slope of 1:1. The flowing discharge is 25 m 3 /sec. Construct
Exercise (3): Open Channel Flow Rapidly Varied Flow 1) A hydraulic jump exists in a trapezoidal channel having a bed width of 7 m and side slope of 1:1. The flowing discharge is 25 m 3 /sec. Construct
HOW FAST/FAR DOES FLY LINE FALL? N. Perkins of the University of Michigan, March 2003
 HOW FAST/FAR DOES FLY LINE FALL? N. Perkins of the University of Michigan, March 003 This report summarizes a simple model for the free fall dynamics of a length of fly line. The line is assumed to remain
HOW FAST/FAR DOES FLY LINE FALL? N. Perkins of the University of Michigan, March 003 This report summarizes a simple model for the free fall dynamics of a length of fly line. The line is assumed to remain
5.8 The Pythagorean Theorem
 5.8. THE PYTHAGOREAN THEOREM 437 5.8 The Pythagorean Theorem Pythagoras was a Greek mathematician and philosopher, born on the island of Samos (ca. 582 BC). He founded a number of schools, one in particular
5.8. THE PYTHAGOREAN THEOREM 437 5.8 The Pythagorean Theorem Pythagoras was a Greek mathematician and philosopher, born on the island of Samos (ca. 582 BC). He founded a number of schools, one in particular
Chapter 3: Trigonometry
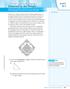
 : Unit 3&4 - Trigonometry Chapter 3: Trigonometry 3.10 Sine or Cosine? Sine Law Cosine Law ASA or AAS SAS ASS SSS Example #1: 12 70 9 Example #2: 17 35 14 1) 2) 3) Solve each triangle ABC. Round answers
: Unit 3&4 - Trigonometry Chapter 3: Trigonometry 3.10 Sine or Cosine? Sine Law Cosine Law ASA or AAS SAS ASS SSS Example #1: 12 70 9 Example #2: 17 35 14 1) 2) 3) Solve each triangle ABC. Round answers
THE EFFECT OF DRAG REDUCING AGENTS ON PRESSURE GRADIENT IN MULTIPHASE, OILIWATER/GAS VERTICAL FLOW. C. KANG AND W. P. JEPSON
 _. -4_JI!I!I!!!!I-== -S------- THE EFFECT OF DRAG REDUCING AGENTS ON PRESSURE GRADIENT IN MULTIPHASE, OILIWATER/GAS VERTICAL FLOW. BY C. KANG AND W. P. JEPSON NSF, IlUCRC, CORROSION IN MULTIPHASE SYSTEMS
_. -4_JI!I!I!!!!I-== -S------- THE EFFECT OF DRAG REDUCING AGENTS ON PRESSURE GRADIENT IN MULTIPHASE, OILIWATER/GAS VERTICAL FLOW. BY C. KANG AND W. P. JEPSON NSF, IlUCRC, CORROSION IN MULTIPHASE SYSTEMS
Mathematics at Work 10
 Nova Scotia Examinations Mathematics at Work 10 QUESTION SAMPLER Notice to users The purpose of this examination sampler is to give students and teachers an idea of the format of the examination. Since
Nova Scotia Examinations Mathematics at Work 10 QUESTION SAMPLER Notice to users The purpose of this examination sampler is to give students and teachers an idea of the format of the examination. Since
CITY OF SIMI VALLEY MEMORANDUM SUBJECT: APPOINTMENT OF SIMI VALLEY COUNCIL ON AGING EXECUTIVE BOARD MEMBERS
 CITY OF SIMI VALLEY MEMORANDUM AGENDA ITEM NO. 3B (1) January 26, 2015 TO: FROM: City Council Department of Community Services SUBJECT: APPOINTMENT OF SIMI VALLEY COUNCIL ON AGING EXECUTIVE BOARD MEMBERS
CITY OF SIMI VALLEY MEMORANDUM AGENDA ITEM NO. 3B (1) January 26, 2015 TO: FROM: City Council Department of Community Services SUBJECT: APPOINTMENT OF SIMI VALLEY COUNCIL ON AGING EXECUTIVE BOARD MEMBERS
Additional Exercises 7.7 Form I Applications Using Rational Equations and Proportions
 Additional Eercises 7.7 Form I Applications Using Rational Equations and Proportions 1. A cyclist bikes at a constant speed for 20 miles. He then returns 1. home at the same speed but takes a different
Additional Eercises 7.7 Form I Applications Using Rational Equations and Proportions 1. A cyclist bikes at a constant speed for 20 miles. He then returns 1. home at the same speed but takes a different
QF 7 Quadratic Application Problems Name:
 1. A watermelon is launched out of the window of an office building, and its path can be modeled by the equation y = 4x 2 + 32x + 15, where y is the watermelon s height (in feet) and x is the time it has
1. A watermelon is launched out of the window of an office building, and its path can be modeled by the equation y = 4x 2 + 32x + 15, where y is the watermelon s height (in feet) and x is the time it has
E9608 Smallbox 1. a(676) m. Line W 16-Aug-96 04:44 to 16-Aug-96 07: W 16-Aug-96 02:41 to 16-Aug-96 04:18.
 E968 Smallbox 1 Line 1 7.6253W 15-Aug-96 23:26 to 16-Aug-96 1:56 2 1 Line 2 7.5556 W 16-Aug-96 2:41 to 16-Aug-96 4:18 2 1 Line 3 7.4834 W 16-Aug-96 4:44 to 16-Aug-96 7:1 2 1 ci a(676) m I IM 4.5 4.4 4.5
E968 Smallbox 1 Line 1 7.6253W 15-Aug-96 23:26 to 16-Aug-96 1:56 2 1 Line 2 7.5556 W 16-Aug-96 2:41 to 16-Aug-96 4:18 2 1 Line 3 7.4834 W 16-Aug-96 4:44 to 16-Aug-96 7:1 2 1 ci a(676) m I IM 4.5 4.4 4.5
t 18 m 4, MCT 4C1 Measurement Test Name: Instructions: Show all of your work. Show a formula step, substitution step, and final answer with units.
 MCT 4C1 Measurement Test Name: Instructions: Show all of your work. Show a formula step, substitution step, and final answer with units. (a) Determine the volume of a square based pyramid with area of
MCT 4C1 Measurement Test Name: Instructions: Show all of your work. Show a formula step, substitution step, and final answer with units. (a) Determine the volume of a square based pyramid with area of
8-5 Angles of Elevation and Depression
 4. HOCKEY A hockey player takes a shot 20 feet away from a 5-foot goal. If the puck travels at a angle of elevation toward the center of the goal, will the player score? 5. MOUNTAINS Find the angle of
4. HOCKEY A hockey player takes a shot 20 feet away from a 5-foot goal. If the puck travels at a angle of elevation toward the center of the goal, will the player score? 5. MOUNTAINS Find the angle of
Pythagorean Theorem in Sports
 Name Date Pythagorean Theorem in Sports Activity 1: Pythagorean Theorem in Baseball Directions: Measure the distance between each of the bases using the yard stick provided. Then convert your measurements
Name Date Pythagorean Theorem in Sports Activity 1: Pythagorean Theorem in Baseball Directions: Measure the distance between each of the bases using the yard stick provided. Then convert your measurements
Implementing Provisions for Art. 411 of the ICR Ski Jumping
 JUMPING HILLS CONSTRUCTION NORM 2018 Implementing Provisions for Art. 411 of the ICR Ski Jumping Author: Hans-Heini Gasser (SUI) EDITION NOVEMBER 2018 Table of Contents Page 1. Preliminary Remarks 3 2.
JUMPING HILLS CONSTRUCTION NORM 2018 Implementing Provisions for Art. 411 of the ICR Ski Jumping Author: Hans-Heini Gasser (SUI) EDITION NOVEMBER 2018 Table of Contents Page 1. Preliminary Remarks 3 2.
77.1 Apply the Pythagorean Theorem
 Right Triangles and Trigonometry 77.1 Apply the Pythagorean Theorem 7.2 Use the Converse of the Pythagorean Theorem 7.3 Use Similar Right Triangles 7.4 Special Right Triangles 7.5 Apply the Tangent Ratio
Right Triangles and Trigonometry 77.1 Apply the Pythagorean Theorem 7.2 Use the Converse of the Pythagorean Theorem 7.3 Use Similar Right Triangles 7.4 Special Right Triangles 7.5 Apply the Tangent Ratio
Trial runs of loading equipment for proposed test of oven wall
 Lehigh University Lehigh Preserve Fritz Laboratory Reports Civil and Environmental Engineering 1955 Trial runs of loading equipment for proposed test of oven wall I. J. Taylor S. J. Errera Follow this
Lehigh University Lehigh Preserve Fritz Laboratory Reports Civil and Environmental Engineering 1955 Trial runs of loading equipment for proposed test of oven wall I. J. Taylor S. J. Errera Follow this
Khosla's theory. After studying a lot of dam failure constructed based on Bligh s theory, Khosla came out with the following;
 Khosla's theory After studying a lot of dam failure constructed based on Bligh s theory, Khosla came out with the following; Following are some of the main points from Khosla's Theory From observation
Khosla's theory After studying a lot of dam failure constructed based on Bligh s theory, Khosla came out with the following; Following are some of the main points from Khosla's Theory From observation
2012 P.A.P.A-2 FREE-RESPONSE QUESTIONS (Calc OK)
 1 P.A.P.A- FREE-RESPONSE QUESTIONS (Calc OK) 1) At the Jackson County Fair held each October, there are many games and attractions which launch things into the air. One game is a football toss where the
1 P.A.P.A- FREE-RESPONSE QUESTIONS (Calc OK) 1) At the Jackson County Fair held each October, there are many games and attractions which launch things into the air. One game is a football toss where the
MATHEMATICAL EVALUATION OF MULTI-LEVEL DIVING
 MATHEMATICAL EVALUATION OF MULTI-LEVEL DIVING by Karl Huggins and Lee Somers MICHU-SG-81-207 MATHEMATICAL EVALUATION OF MULI-LEVEL DIVING by Karl E. Huggins Assistant in Research University of Michigan
MATHEMATICAL EVALUATION OF MULTI-LEVEL DIVING by Karl Huggins and Lee Somers MICHU-SG-81-207 MATHEMATICAL EVALUATION OF MULI-LEVEL DIVING by Karl E. Huggins Assistant in Research University of Michigan
Critical Velocity/ Nodal Stability Gas Well Predictions
 Originally Presented at: Gas Well De-Liquification Workshop Adams Mark Hotel, Denver, Colorado March 5-7, 2007 European Conference Gas Well Deliquification 25-2626 September 2007 Critical Velocity/ Nodal
Originally Presented at: Gas Well De-Liquification Workshop Adams Mark Hotel, Denver, Colorado March 5-7, 2007 European Conference Gas Well Deliquification 25-2626 September 2007 Critical Velocity/ Nodal
1. Five more than three times a number x. 3. Seventeen percent of a number x.
 Pre-Calculus: 1.7.1 Mastery Practice Name: Date Period Write a mathematical expression for the quantity described verbally: 1. Five more than three times a number x. 3. Seventeen percent of a number x.
Pre-Calculus: 1.7.1 Mastery Practice Name: Date Period Write a mathematical expression for the quantity described verbally: 1. Five more than three times a number x. 3. Seventeen percent of a number x.
The Pythagorean Theorem Diamond in the Rough
 The Pythagorean Theorem SUGGESTED LEARNING STRATEGIES: Shared Reading, Activating Prior Knowledge, Visualization, Interactive Word Wall Cameron is a catcher trying out for the school baseball team. He
The Pythagorean Theorem SUGGESTED LEARNING STRATEGIES: Shared Reading, Activating Prior Knowledge, Visualization, Interactive Word Wall Cameron is a catcher trying out for the school baseball team. He
Continuous Flow Gas Lift Design By Jack R. Blann 2/9/2008 1
 Continuous Flow Gas Lift Design By Jack R. Blann 1 2 Petroleum Engineering Handbook Gas Lift appears as Chapter 12 in: Volume IV Production Operations Engineering Edited by Joe Dunn Clegg Chapter 12 was
Continuous Flow Gas Lift Design By Jack R. Blann 1 2 Petroleum Engineering Handbook Gas Lift appears as Chapter 12 in: Volume IV Production Operations Engineering Edited by Joe Dunn Clegg Chapter 12 was
word problems.notebook May 27, 2016
 Word Problems: When solving word problems you can use vertex form, factored form or standard form to create an algebraic model of the situation. Use the form that is most helpful for the context of the
Word Problems: When solving word problems you can use vertex form, factored form or standard form to create an algebraic model of the situation. Use the form that is most helpful for the context of the
2011 Excellence in Mathematics Contest Team Project Level I (Precalculus and above)
 011 Excellence in Mathematics Contest Team Project Level I (Precalculus and above) School Name: Solutions Group Members: Reference Sheet Formulas and Facts You may need to use some of the following formulas
011 Excellence in Mathematics Contest Team Project Level I (Precalculus and above) School Name: Solutions Group Members: Reference Sheet Formulas and Facts You may need to use some of the following formulas
6.3 Unit Conversion: American System
 6.3. UNIT CONVERSION: AMERICAN SYSTEM 467 6.3 Unit Conversion: American System In this section we will develop a technique for converting units used in the American system. We begin with a discussion of
6.3. UNIT CONVERSION: AMERICAN SYSTEM 467 6.3 Unit Conversion: American System In this section we will develop a technique for converting units used in the American system. We begin with a discussion of
Reynolds Technology Ltd
 Reynolds Technology Ltd Reynolds Technology Ltd, Building 21, Shaftmoor Industrial Estate, 226 Shaftmoor Lane, Hall Green, Birmingham B28 8SP Cycle Frame Tube Price List - 1st January 2017 Payment by TT,
Reynolds Technology Ltd Reynolds Technology Ltd, Building 21, Shaftmoor Industrial Estate, 226 Shaftmoor Lane, Hall Green, Birmingham B28 8SP Cycle Frame Tube Price List - 1st January 2017 Payment by TT,
Math A Regents Exam 0806 Page 1
 Math A Regents Exam 0806 Page 1 1. 080601a, P.I. A.N.1 While solving the equation 4( x + 2) = 28, Becca wrote 4x + 8= 28. Which property did she use? [A] associative [B] commutative [C] identity [D] distributive
Math A Regents Exam 0806 Page 1 1. 080601a, P.I. A.N.1 While solving the equation 4( x + 2) = 28, Becca wrote 4x + 8= 28. Which property did she use? [A] associative [B] commutative [C] identity [D] distributive
Math 081 Worksheet Section 5.4 v01 Spring 2011 Dressler. Name
 Math 081 Worksheet Section 5. v01 Spring 2011 Dressler Name Solve. 1) The ratio of a quarterback's completed passes to attempted passes is 5 to 6. If he attempted 2 passes, find how many passes he completed.
Math 081 Worksheet Section 5. v01 Spring 2011 Dressler Name Solve. 1) The ratio of a quarterback's completed passes to attempted passes is 5 to 6. If he attempted 2 passes, find how many passes he completed.
Projectile Motion applications
 Projectile Motion applications 1. A stone is thrown horizontally at a speed of 10.0 m/s from the top of a cliff 78.4 m high. a. How long does it take the stone to reach the bottom of the cliff? b. How
Projectile Motion applications 1. A stone is thrown horizontally at a speed of 10.0 m/s from the top of a cliff 78.4 m high. a. How long does it take the stone to reach the bottom of the cliff? b. How
CIRCUMFERENCE ~D AREA OF A CIRCLE. remember that the diameter = 2 x radius. , Circumference of a :circle = 11 x diameter DATE: PERIOD: N~ :
 CIRCUMFERENCE ~D I AREA OF A CIRCLE, Circumference of a :circle = 11 x diameter remember that the diameter = 2 x radius N~ : DATE: PERIOD: A circle is all points in the same plane that lie at an equal
CIRCUMFERENCE ~D I AREA OF A CIRCLE, Circumference of a :circle = 11 x diameter remember that the diameter = 2 x radius N~ : DATE: PERIOD: A circle is all points in the same plane that lie at an equal
Strawkets and Quadratics
 Strawkets and Quadratics Summary In this activity, the students will develop a quadratic function for their rocket flight. Each student will construct a paper rocket that he/she will launch by blowing
Strawkets and Quadratics Summary In this activity, the students will develop a quadratic function for their rocket flight. Each student will construct a paper rocket that he/she will launch by blowing
2018 Chapter Competition Countdown Round Problems 1 80
 2018 Chapter Competition Countdown Round Problems 1 80 This booklet contains problems to be used in the Countdown Round. 2018 MATHCOUNTS National Competition Sponsor National Sponsors Raytheon Company
2018 Chapter Competition Countdown Round Problems 1 80 This booklet contains problems to be used in the Countdown Round. 2018 MATHCOUNTS National Competition Sponsor National Sponsors Raytheon Company
ACTIVITY: Finding a Formula Experimentally
 8.1 Volumes of Cylinders How can you find the volume of a cylinder? 1 ACTIVITY: Finding a Formula Experimentally Work with a partner. a. Find the area of the face of a coin. b. Find the volume of a stack
8.1 Volumes of Cylinders How can you find the volume of a cylinder? 1 ACTIVITY: Finding a Formula Experimentally Work with a partner. a. Find the area of the face of a coin. b. Find the volume of a stack
8-1. The Pythagorean Theorem and Its Converse. Vocabulary. Review. Vocabulary Builder. Use Your Vocabulary
 8-1 he Pythagorean heorem and Its Converse Vocabulary Review 1. Write the square and the positive square root of each number. Number Square Positive Square Root 9 81 3 1 4 1 16 1 2 Vocabulary Builder leg
8-1 he Pythagorean heorem and Its Converse Vocabulary Review 1. Write the square and the positive square root of each number. Number Square Positive Square Root 9 81 3 1 4 1 16 1 2 Vocabulary Builder leg
Relative Motion. A look at "Frames of Reference" Website
 Name Relative Motion A look at "Frames of Reference" Website http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=140.msg704#msg704 Introduction An object may appear to have one motion to one observer and
Name Relative Motion A look at "Frames of Reference" Website http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=140.msg704#msg704 Introduction An object may appear to have one motion to one observer and
Math 110 Sec 6.2 Proportions. Name Find the unit price. (Sec 6.1) 1) $52.00 for 5 compact discs. 2) $0.90 for 2 onions
 Math 110 Sec 6.2 Proportions Name Find the unit price. (Sec 6.1) 1) $52.00 for 5 compact discs 2) $0.0 for 2 onions Find the unit price and decide which is the better buy. Round to three decimal places.
Math 110 Sec 6.2 Proportions Name Find the unit price. (Sec 6.1) 1) $52.00 for 5 compact discs 2) $0.0 for 2 onions Find the unit price and decide which is the better buy. Round to three decimal places.
MI 4 Project on Parametric Equations. Parametric Worksheet
 (To be done just before project is assigned.) Parametric Worksheet 1. From its initial position at (3,4), an object moves linearly, reaching (9, 8) after two seconds and (15, 12) after four seconds. a.
(To be done just before project is assigned.) Parametric Worksheet 1. From its initial position at (3,4), an object moves linearly, reaching (9, 8) after two seconds and (15, 12) after four seconds. a.
NYC Marathon Quarter 1 Review Task. The New York City Marathon was last weekend. Over 50,000 people ran 26.2 miles around the city!
 NYC Marathon Quarter 1 Review Task Name: Alg: The New York City Marathon was last weekend. Over 50,000 people ran 26.2 miles around the city! 1. The 2015 male winner was Stanely Biwott, his time was 2
NYC Marathon Quarter 1 Review Task Name: Alg: The New York City Marathon was last weekend. Over 50,000 people ran 26.2 miles around the city! 1. The 2015 male winner was Stanely Biwott, his time was 2
Pressure Measurement
 Pressure Measurement Absolute and Gage Pressure P abs = P gage + P atm where P abs = Absolute pressure P abs = Gage pressure P abs = atmospheric pressure A perfect vacuum is the lowest possible pressure.
Pressure Measurement Absolute and Gage Pressure P abs = P gage + P atm where P abs = Absolute pressure P abs = Gage pressure P abs = atmospheric pressure A perfect vacuum is the lowest possible pressure.
Why do fish float upward when they die if their weight is slightly greater than the buoyant force?
 From Warmup That's how fish go up and down in water! But by that mechanism, would Marlin and Dory really have been able to go so deep in the ocean in search of Nemo? I doubt it but I don t know for sure.
From Warmup That's how fish go up and down in water! But by that mechanism, would Marlin and Dory really have been able to go so deep in the ocean in search of Nemo? I doubt it but I don t know for sure.
Physics for Scientist and Engineers third edition Kinematics 1-D
 Kinematics 1-D The position of a runner as a function of time is plotted along the x axis of a coordinate system. During a 3.00 s time interval, the runner s position changes from x1=50.0 m to x2= 30.5
Kinematics 1-D The position of a runner as a function of time is plotted along the x axis of a coordinate system. During a 3.00 s time interval, the runner s position changes from x1=50.0 m to x2= 30.5
Course 2 Unit 1 Practice
 Course Unit 1 Practice Lesson 1-1 1. Estimate each sum or difference to the nearest unit. $8.56 1 $.35 $3.95. Find each sum or difference. 7.8 1 15.6 1 9.509 b. 0.37 1.083 b. 13.65.5 c. 8 0.057 d. 8.97
Course Unit 1 Practice Lesson 1-1 1. Estimate each sum or difference to the nearest unit. $8.56 1 $.35 $3.95. Find each sum or difference. 7.8 1 15.6 1 9.509 b. 0.37 1.083 b. 13.65.5 c. 8 0.057 d. 8.97
Sept 23, 2014 LAB MANUAL
 Sept 23, 2014 LAB MANUAL 1000.0 1000 STANDARD PRACTICES 1000.1 CALCULATIONS and FORMS Throughout this manual there are test calculation procedures. These calculations are provided so that a technician
Sept 23, 2014 LAB MANUAL 1000.0 1000 STANDARD PRACTICES 1000.1 CALCULATIONS and FORMS Throughout this manual there are test calculation procedures. These calculations are provided so that a technician
2011 Excellence in Mathematics Contest Team Project Level I (Precalculus and above) School Name: Group Members:
 011 Excellence in Mathematics Contest Team Project Level I (Precalculus and above) School Name: Group Members: Reference Sheet Formulas and Facts You may need to use some of the following formulas and
011 Excellence in Mathematics Contest Team Project Level I (Precalculus and above) School Name: Group Members: Reference Sheet Formulas and Facts You may need to use some of the following formulas and
1 Teaching Objective(s) *Lesson plan designed for1-2 days Mississippi Mathematics Framework The student will: 2 Instructional Activities
 ! "# $!%& 1 Teaching Objective(s) *Lesson plan designed for1-2 days Mississippi Mathematics Framework 2000-2005 The student will: 4a. write ratios comparing given data 4c. solve proportions 2 Instructional
! "# $!%& 1 Teaching Objective(s) *Lesson plan designed for1-2 days Mississippi Mathematics Framework 2000-2005 The student will: 4a. write ratios comparing given data 4c. solve proportions 2 Instructional
PHYSICS Unit 2 Key Topic Test 1 Aspects of Motion QUESTION BOOK. Student Name:
 Student Name: PHYSICS 2014 Unit 2 Key Topic Test 1 Aspects of Motion Recommended writing time*: 45 minutes Total number of marks available: 45 marks QUESTION BOOK SECTION A MULTIPLE-CHOICE QUESTIONS SECTION
Student Name: PHYSICS 2014 Unit 2 Key Topic Test 1 Aspects of Motion Recommended writing time*: 45 minutes Total number of marks available: 45 marks QUESTION BOOK SECTION A MULTIPLE-CHOICE QUESTIONS SECTION
Unit 4: Projectiles ( Angled Projectiles )
 Unit 4: Projectiles ( Angled Projectiles ) When dealing with a projectile that is not launched/thrown perfectly horizontal, you must start by realizing that the initial velocity has two components: an
Unit 4: Projectiles ( Angled Projectiles ) When dealing with a projectile that is not launched/thrown perfectly horizontal, you must start by realizing that the initial velocity has two components: an
EQ: How do I use trigonometry to find missing side lengths of right triangles?
 EQ: How do I use trigonometry to find missing side lengths of right triangles? Essential Question Essential Question Essential Question Essential Question Essential Question Essential Question Essential
EQ: How do I use trigonometry to find missing side lengths of right triangles? Essential Question Essential Question Essential Question Essential Question Essential Question Essential Question Essential
MATH 227 CP 3 SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
 MATH 227 CP 3 SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. Find the mean for the given sample data. Unless indicated otherwise, round your answer to
MATH 227 CP 3 SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. Find the mean for the given sample data. Unless indicated otherwise, round your answer to
CATALINA SWIM SPAS OLYMPIC 400 SERIES
 CATALINA SWIM SPAS OLYMPIC 400 SERIES DEALER PRICE LIST 11/1/2015-11/1/2016 12.6 REGATTA MODEL DESCRIPTION ELEC PUMPS DIMENSIONS PRICE C400-Bronze 12.6 Portable BP3 (1) 5 HP & (2) 4 HP Pumps 90 x 151 x
CATALINA SWIM SPAS OLYMPIC 400 SERIES DEALER PRICE LIST 11/1/2015-11/1/2016 12.6 REGATTA MODEL DESCRIPTION ELEC PUMPS DIMENSIONS PRICE C400-Bronze 12.6 Portable BP3 (1) 5 HP & (2) 4 HP Pumps 90 x 151 x
Technical Report Culvert A Hydraulic Analysis
 DATE: November 3, 2011 Technical Report Culvert A Hydraulic Analysis TO: FROM: RE: Jim Reiser, P.E. Project Manager Parsons Brinckerhoff, Inc. Kurt Killian, P.E., CFM Parsons Brinckerhoff, Inc. Design
DATE: November 3, 2011 Technical Report Culvert A Hydraulic Analysis TO: FROM: RE: Jim Reiser, P.E. Project Manager Parsons Brinckerhoff, Inc. Kurt Killian, P.E., CFM Parsons Brinckerhoff, Inc. Design
Practice 9-1. The Real Numbers. Write all names that apply to each number
 Chapter 9 Practice 9-1 The Real Numbers Write all names that apply to each number. 1. 3.2 2. 2 5 3. 12 4. 4 2 5. 20 6. 16 7. 7 8 8. 0.15 9. 18 2 10. 45 11. 25 12. 6.75 State if the number is rational,
Chapter 9 Practice 9-1 The Real Numbers Write all names that apply to each number. 1. 3.2 2. 2 5 3. 12 4. 4 2 5. 20 6. 16 7. 7 8 8. 0.15 9. 18 2 10. 45 11. 25 12. 6.75 State if the number is rational,
Sample Grade 7 End-of-Unit Assessment: Proportional Reasoning
 Sample Grade 7 End-of-Unit Assessment: Proportional Reasoning Name: Date: I can determine unit rates and scale factors. 1. Find the unit rate: 40 feet in 1 minute. 1 point. Find the unit rate: $8.40 for
Sample Grade 7 End-of-Unit Assessment: Proportional Reasoning Name: Date: I can determine unit rates and scale factors. 1. Find the unit rate: 40 feet in 1 minute. 1 point. Find the unit rate: $8.40 for
Physics 1 HW #8: Chapter 3
 Phsics 1 HW #8: Chapter 3 Problems 6-9, 31, 3, 49, 54. For EVERY one of the problems, draw ector diagrams, labeling the ectors and write out the ector equation! Hae fun! 3.6 We use the following notation:
Phsics 1 HW #8: Chapter 3 Problems 6-9, 31, 3, 49, 54. For EVERY one of the problems, draw ector diagrams, labeling the ectors and write out the ector equation! Hae fun! 3.6 We use the following notation:
Lesson 22: Getting the Job Done Speed, Work, and Measurement Units
 Lesson 22: Getting the Job Done Speed, Work, and Measurement Units Student Outcomes Students decontextualize a given speed situation, representing symbolically the quantities involved with the formula.
Lesson 22: Getting the Job Done Speed, Work, and Measurement Units Student Outcomes Students decontextualize a given speed situation, representing symbolically the quantities involved with the formula.
Midterm Exam: Making a Study Guide
 Name: Class: Physics Teacher: Mr. Szopiak Date: Midterm Exam: Making a Study Guide This worksheet will help you and your classmates put together a pretty comprehensive guide to your midterm studying. Your
Name: Class: Physics Teacher: Mr. Szopiak Date: Midterm Exam: Making a Study Guide This worksheet will help you and your classmates put together a pretty comprehensive guide to your midterm studying. Your
Addition and Subtraction of Rational Expressions
 RT.3 Addition and Subtraction of Rational Expressions Many real-world applications involve adding or subtracting algebraic fractions. Similarly as in the case of common fractions, to add or subtract algebraic
RT.3 Addition and Subtraction of Rational Expressions Many real-world applications involve adding or subtracting algebraic fractions. Similarly as in the case of common fractions, to add or subtract algebraic
OFFICE OF STRUCTURES MANUAL FOR HYDROLOGIC AND HYDRAULIC DESIGN CHAPTER 11 APPENDIX B TIDEROUT 2 USERS MANUAL
 OFFICE OF STRUCTURES MANUAL FOR HYDROLOGIC AND HYDRAULIC DESIGN CHAPTER 11 APPENDIX B TIDEROUT 2 USERS MANUAL APRIL 2011 APRIL 2011 Page 1 Preface TIDEROUT 2, Build 1.22 dated June 29, 2006 is the current
OFFICE OF STRUCTURES MANUAL FOR HYDROLOGIC AND HYDRAULIC DESIGN CHAPTER 11 APPENDIX B TIDEROUT 2 USERS MANUAL APRIL 2011 APRIL 2011 Page 1 Preface TIDEROUT 2, Build 1.22 dated June 29, 2006 is the current
Plan B Dam Breach Assessment
 Plan B Dam Breach Assessment Introduction In support of the Local Sponsor permit applications to the states of Minnesota and North Dakota, a dam breach analysis for the Plan B alignment of the Fargo-Moorhead
Plan B Dam Breach Assessment Introduction In support of the Local Sponsor permit applications to the states of Minnesota and North Dakota, a dam breach analysis for the Plan B alignment of the Fargo-Moorhead
I can add vectors together. IMPORTANT VOCABULARY
 Pre-AP Geometry Chapter 9 Test Review Standards/Goals: G.SRT.7./ H.1.b.: I can find the sine, cosine and tangent ratios of acute angles given the side lengths of right triangles. G.SRT.8/ H.1.c.: I can
Pre-AP Geometry Chapter 9 Test Review Standards/Goals: G.SRT.7./ H.1.b.: I can find the sine, cosine and tangent ratios of acute angles given the side lengths of right triangles. G.SRT.8/ H.1.c.: I can
GOING MY WAY EXAMPLES
 GOING MY WAY EXAMPLES When an object moves at a constant speed, or rate, it is said to be in uniform motion. The formula d = rt is used to solve uniform motion problems. In the formula, d represents distance,
GOING MY WAY EXAMPLES When an object moves at a constant speed, or rate, it is said to be in uniform motion. The formula d = rt is used to solve uniform motion problems. In the formula, d represents distance,
LEARNING OBJECTIVES. Overview of Lesson. guided practice Teacher: anticipates, monitors, selects, sequences, and connects student work
 D Rate, Lesson 1, Conversions (r. 2018) RATE Conversions Common Core Standard N.Q.A.1 Use units as a way to understand problems and to guide the solution of multi-step problems; choose and interpret units
D Rate, Lesson 1, Conversions (r. 2018) RATE Conversions Common Core Standard N.Q.A.1 Use units as a way to understand problems and to guide the solution of multi-step problems; choose and interpret units
Week 1, Lesson 2 1. Warm up 2. Notes Quadratics 3. ICA Physics Rocket
 Do all functions follow patterns? Essential Question Essential Question Essential Question Essential Question Essential Question Essential Question Essential Question Week 1, Lesson 2 1. Warm up 2. Notes
Do all functions follow patterns? Essential Question Essential Question Essential Question Essential Question Essential Question Essential Question Essential Question Week 1, Lesson 2 1. Warm up 2. Notes
Honors Assignment - Vectors
 Honors Assignment - Vectors Reading Chapter 3 Homework Assignment #1: Read Chap 3 Sections 1-3 M: #2, 3, 5 (a, c, f), 6-9 Homework Assignment #2: M: #14, 15, 16, 18, 19 Homework Assignment #3: Read Chap
Honors Assignment - Vectors Reading Chapter 3 Homework Assignment #1: Read Chap 3 Sections 1-3 M: #2, 3, 5 (a, c, f), 6-9 Homework Assignment #2: M: #14, 15, 16, 18, 19 Homework Assignment #3: Read Chap
MATH 110 Sample 02 Exam 1
 1. Evaluate: log 4 64 [A] 3 [B] 1 12 [C] 12 [D] 1 3 2. Given log 5 = T and log 2 = U, find log. [A] T + U [B] TU [C] T + U [D] TU. 3. Find x if e x 52 8 =, and ou are given ln 8 = 2.0794. [A] 0.3999 [B]
1. Evaluate: log 4 64 [A] 3 [B] 1 12 [C] 12 [D] 1 3 2. Given log 5 = T and log 2 = U, find log. [A] T + U [B] TU [C] T + U [D] TU. 3. Find x if e x 52 8 =, and ou are given ln 8 = 2.0794. [A] 0.3999 [B]
{Recall that 88 ft = 60 mi so 88 ft x h = 1 s h s 60 mi General Atomics Sciences Education Foundation All rights reserved.
 Simulation Tool Development 1. a. Develop a scale model car tat sows te distance traveled in 1 s at speeds from 10 to 70 mp in increments of 10 mp. Use a scale of 1 in = 100 ft. Include a marker on eac
Simulation Tool Development 1. a. Develop a scale model car tat sows te distance traveled in 1 s at speeds from 10 to 70 mp in increments of 10 mp. Use a scale of 1 in = 100 ft. Include a marker on eac
3/27/18 CCM6+ Review Units 8 11 for Q3 RETEST tomorrow. HW: study units 8 11 for retest tomorrow!
 3/27/18 CCM6+ Review Units 8 11 for Q3 RETEST tomorrow. HW: study units 8 11 for retest tomorrow! 1 Tests back...questions? 2 Unit 8: Expressions and Inequalities 3 Solve for m: _m_ = 40 5 4 Solve for
3/27/18 CCM6+ Review Units 8 11 for Q3 RETEST tomorrow. HW: study units 8 11 for retest tomorrow! 1 Tests back...questions? 2 Unit 8: Expressions and Inequalities 3 Solve for m: _m_ = 40 5 4 Solve for
Warm up # 20. Table of Contents TC1
 Warm up # 20 Try and describe where something is located in class. Table of Contents TC1 Assignments Page # 7. Textbook scavenger hunt 8. Bubble gum lab 9. Averages 10. Scientific method quiz 11. Motion
Warm up # 20 Try and describe where something is located in class. Table of Contents TC1 Assignments Page # 7. Textbook scavenger hunt 8. Bubble gum lab 9. Averages 10. Scientific method quiz 11. Motion
8-1. The Pythagorean Theorem and Its Converse. Vocabulary. Review. Vocabulary Builder. Use Your Vocabulary
 8-1 The Pythagorean Theorem and Its Converse Vocabulary Review 1. Write the square and the positive square root of each number. Number 9 Square Positive Square Root 1 4 1 16 Vocabulary Builder leg (noun)
8-1 The Pythagorean Theorem and Its Converse Vocabulary Review 1. Write the square and the positive square root of each number. Number 9 Square Positive Square Root 1 4 1 16 Vocabulary Builder leg (noun)
Do not turn this page until you are asked to.
 YEAR 7 MATHEMATICS EXAMINATION SEMESTER 2 2016 QUESTION AND ANSWER BOOKLET STUDENT NAME: TEACHER: DATE: TIME ALLOWED FOR THIS PAPER Reading time before commencing work: 10 minutes Working time for this
YEAR 7 MATHEMATICS EXAMINATION SEMESTER 2 2016 QUESTION AND ANSWER BOOKLET STUDENT NAME: TEACHER: DATE: TIME ALLOWED FOR THIS PAPER Reading time before commencing work: 10 minutes Working time for this
