Permutations and Combinations
|
|
|
- Christiana Cooper
- 6 years ago
- Views:
Transcription
1 13 Pemutatios ad Combiatios TERMINOLOGY Aagemets: Diffeet ways of ogaisig objects Combiatios: Aagemets of objects without eplacemet o epetitio whe ode is ot impotat. The otatio used is C fo selectig objects fom whee ode does t matte Factoial: A factoial is the poduct of cosecutive positive iteges fom dow to oe. Fo example 6! 6 x 5 x 4 x 3 x 2 x 1 Fudametal coutig piciple: If oe evet ca occu i p ways ad a secod idepedet evet ca occu i q ways, the the two successive evets ca occu i p x q diffeet ways Odeed selectios: Selectios that ae take i a paticula positio Pemutatios: The aagemet of objects without eplacemet o epetitio whe ode is impotat. The otatio used is P fo selectig objects fom whee ode mattes Radom expeimets: Expeimets that ae made with o patte o ode whee each outcome is equally likely to occu Sample space: The set of all possible outcomes i a evet o seies of evets Uodeed selectios: Selectios that ae made whe the ode of aagemets is ot impotat o elevat
2 Chapte 13 Pemutatios ad Combiatios 717 INTRODUCTION THIS CHAPTER IS AN itoductio to some of the cocepts you will meet i pobability i the HSC Couse. Pobability is the study of how likely it is that somethig will happe. It is used to make pedictios i diffeet aeas, agig fom games of chace to busiess decisio-makig. I this chapte you will study geeal coutig techiques based o the fudametal coutig piciple. These will lead o to the study of pemutatios ad combiatios. These have applicatios i fidig the size of the sample space, o the ways that cetai evets ca happe i pobability. It ca also tell us the umbe of postcodes a state ca have, the umbe of telephoe umbes that is possible i a city ad the umbe of combiatios makig up seial umbes fo appliaces. Fudametal Coutig Piciple Simple pobability You have studied pobability i ealie stages of mathematics. We ca measue pobability i theoy. Howeve, pobability oly gives us a appoximate idea of the likelihood of cetai evets happeig. Fo example, i Lotto daws, thee is a machie that daws out the balls at adom ad a pael of supevisos checks that this happes popely. Each ball is idepedet of the othes ad is equally likely to be daw out. I a hose ace, it is difficult to measue pobability as the hoses ae ot all equally likely to wi. Othe factos such as ability, taiig, expeiece ad weight of the jockey all affect it. The likelihood of ay oe hose wiig is ot adom. The pobability of a evet E happeig, P ( E ), is give by the umbe of ways the evet ca occu, ( E ), compaed with the total umbe of outcomes possible ( S ) (the size of the sample space). E ( ) P ] Eg S () If PE ] g 0 the evet is impossible. If PE ] g 1 the evet is cetai (it has to happe). 0 # PE ] g # 1
3 718 Maths I Focus Mathematics Extesio 1 Pelimiay Couse The sum of all pobabilities is 1. Complemetay evets: P] ot Eg 1 P] Eg o P^L Eh 1 - P( E) whee L E is the complemet of E PE ] g + PE ^L h 1 EXAMPLES 1. Aliso buys 5 affle tickets ad 100 ae sold altogethe. What is the pobability that Aliso (a) wis (b) does t wi fist pize i the affle? (a) The size of the sample space, o total umbe of outcomes is 100, sice thee ae 100 tickets altogethe. Aliso has 5 tickets so has 5 diffeet ways of wiig the affle. 5 P ( Wi ) (b) Thee ae o 95 othe tickets that could wi if Aliso loses. 95 P ( Loss ) O, if we kow that the sum of all pobabilities is 1, we could say P( Loss) 1 - P( Wi) Thee ae 56 books o music at the school libay ad thee ae 2000 books altogethe. If Athoy selects a book at adom, fid the pobability that it will be a book o music. The size of the sample space is 2000 ad thee ae 56 ways that Athoy could select a music book. 56 P ( Music book )
4 Chapte 13 Pemutatios ad Combiatios Execises 1. A lottey is held i which tickets ae sold. If I buy 2 tickets, what is the pobability of my wiig the pize i the lottey? 2. The pobability of a bus aivig 17 o time is estimated at. What 33 is the pobability that the bus will ot aive o time? 3. The pobability of a seed poducig a pik flowe is 9 7. Fid the pobability that the seed will poduce a diffeet coloued flowe. 7. A shoe shop odes i 20 pais of black, 14 pais of avy ad 3 pais of bow school shoes. If the boxes ae all mixed up, fid the pobability that oe box selected at adom will cotai bow shoes. 8. A biased coi is weighted so that heads comes up twice as ofte as tails. Fid the pobability of tossig a tail. 9. A die has the cete dot paited white o the 5 so that it appeas as a 4. Fid the pobability of ollig (a) a 2 (b) a 4 (c) a umbe less tha I a lottey, tickets ae sold. If Lucia buys 10 tickets, what is the pobability of he wiig fist pize? 5. A machie has a 1.5% chace of beakig dow at ay give time. What is the pobability of the machie ot beakig dow? 6. A bag cotais 6 ed balls ad 8 white balls. If oe ball is daw out at adom, fid the pobability that it will be (a) white (b) ed. 10. A book has 124 pages. If the book is opeed at ay page at adom, fid the pobability of the page umbe beig (a) eithe 80 o 90 (b) a multiple of 10 (c) a odd umbe (d) less tha I the game of pool, thee ae 15 balls, each with the umbe 1 to 15 o it. I Kelly Pool, each peso chooses a umbe at adom fom a cotaie ad has to ty ad sik the ball with the coespodig umbe. If Tacey chooses a umbe, fid the pobability that he ball will be (a) the eight ball (b) a odd umbe (c) a umbe less tha 10. A multiple of 10 is a umbe that is divisible by 10.
5 720 Maths I Focus Mathematics Extesio 1 Pelimiay Couse 12. A box cotaiig a light globe 1 has a pobability of holdig 20 a defective globe. If 160 boxes ae checked, how may globes would be expected to be defective? 13. Thee ae 29 ed, 17 blue, 21 yellow ad 19 gee jelly beas i a packet. If Kate chooses oe at adom, fid the pobability that it will be (a) ed (b) blue o yellow (c) ot gee. 14. The pobability of beedig a 2 white budgie is. If M Seed 15 beeds 240 budgies ove the yea, how may would be expected to be white? 15. A die is olled. Calculate the pobability of ollig (a) a 6 (b) a eve umbe (c) a umbe less tha 3 (d) 4 o moe (e) a multiple of The pobability that a aow will 13 hit a taget is. 18 (a) Fid the pobability that it will miss the taget. (b) If 126 aows ae fied, how may would be expected to hit a taget? 17. A dog ca catch a ball i its mouth 8 times out of 10. (a) What is the pobability of the dog catchig a ball? (b) If the ball is thow to the dog 45 times, how may times would the dog be expected to catch it? 18. I a bag thee ae 21 lollies with pik wappes ad 23 with blue wappes. If Leila chooses a lolly at adom fom the bag, fid the pobability that she selects a lolly with (a) a blue wappe (b) a pik wappe. 19. I a suvey, it was foud that 18 people pefeed Bad A of soft dik while 39 people pefeed Bad B. What is the pobability that a peso chose at adom pefes Bad A? 20. A school has 653 juio ad 329 seio studets. If a studet is chose at adom, what is the pobability that it will be a seio studet? 21. A class has 12 gils ad 19 boys. Eight of the gils ad 12 of the boys play a spot. If a studet is chose at adom, fid the pobability that the peso chose (a) is a boy (b) plays a spot (c) is a gil who does t play a spot (d) does t play a spot. 22. Amie s CD collectio icludes 21 R&B, 14 ock ad 24 jazz albums. If she selects oe CD to play at adom, fid the pobability that the CD is (a) ock (b) R&B o ock (c) jazz (d) ot R&B.
6 Chapte 13 Pemutatios ad Combiatios The pobability of wiig a game of chace is 8 3 ad the 5 pobability of losig is. What 12 is the pobability of a daw? 24. I a poll, 39% said they would vote Labo, 34% said they would vote Libeal ad 8% said they would vote fo idepedets o small paties. What pecetage would vote fo Gees? 25. A aow has a 0.37 pobability of hittig a taget outside the bullseye zoe ad 0.12 pobability of missig the taget altogethe. What is the pobability of the aow hittig the bullseye aea? Coutig techiques I the HSC Couse you will lea about multi-stage evets (evets whee thee ae two o moe evets such as ollig two dice o tossig two cois). The coutig ca become quite difficult, which is why we itoduce coutig techiques i the Pelimiay Couse. Class Discussio Beak up ito pais ad ty these expeimets with oe doig the activity ad oe ecodig the esults. 1. Toss two cois as may times as you ca i a 5-miute peiod ad ecod the esults i the table: Result Two heads Oe head ad oe tail Two tails Tally Compae you esults with othes i the class. What do you otice? Is this supisig? 2. Roll two dice as may times as you ca i a 5-miute peiod, fid the total of the two uppemost umbes o the dice ad ecod the esults i the table: Total Tally Compae you esults with othes i the class. What do you otice? Is this supisig? Why do t these esults appea to be equally likely?
7 722 Maths I Focus Mathematics Extesio 1 Pelimiay Couse Thee ae may examples of whee coutig techiques ae useful, i pobability ad i aeas such as maufactuig, busiess, biology ad ecoomics. Fo example, i geetics, the umbe of molecules o DNA stads ca be difficult to fid. Ivestigatio 1. To tavel to wok, Cassie eeds to catch a bus ad a tai. She lives ea a bus stop ad thee ae thee diffeet buses she could catch ito tow. Whe she aives i tow, she eeds to catch oe of fou tais to wok. If thee ae thee buses ad fou tais possible fo Cassie to catch, i how may ways is it possible fo he to tavel to wok? Buses Tais Cassie s house A 1 2 B 3 C 4 2. At a estauat, thee ae thee etees, fou mai meals ad two dessets. Evey time Rick eats at the estauat he chooses to eat a diffeet combiatio of couses. How may times would he eed to go to the estauat to cove all possible combiatios? FUNDAMENTAL COUNTING PRINCIPLE If oe evet ca happe i a diffeet ways, a secod evet ca happe i b diffeet ways, a thid i c diffeet ways ad so o, the these successive evets ca happe i abc diffeet ways. EXAMPLES 1. A pesoal idetificatio umbe (PIN) has 4 lettes followed by 3 umbes. How may diffeet PINs of this type ae possible? Thee ae 26 lettes ad 10 umbes ( 0 9 ) possible fo the positios i the PIN.
8 Chapte 13 Pemutatios ad Combiatios 723 Total umbe 26# 26# 26# 26# 10# 10# # So PINs ae possible. 2. A estauat seves 5 diffeet types of etee, 12 mai couses ad 6 dessets. (a) If I ode ay combiatio of etee, mai couse ad desset at adom, how may diffeet combiatios ae possible? (b) If my fied makes 3 guesses at which combiatio I will ode, what is the pobability that she will guess coectly? (a) Total umbe of combiatios 5# 12# (b) P ^coect guess h Hee ae some examples of coutig whe thee is o epetitio o eplacemet. EXAMPLES 1. To wi a tifecta i a ace, a peso has to pick the hoses that come fist, secod ad thid i the ace. If a ace has 9 hoses, how may diffeet combiatios could be a tifecta? Ay of the 9 hoses could come fist. Ay of the emaiig 8 could come secod. Ay of the emaiig 7 hoses could come thid. Total ways 9# 8 # The pobabilities will be diffeet fo whee each hose will come i the ace, but the umbe of possible diffeet tifecta combiatios will be the same. CONTINUED
9 724 Maths I Focus Mathematics Extesio 1 Pelimiay Couse 2. A goup of 15 people atted a cocet ad 3 of them ae adomly give a fee backstage pass. The fist peso eceives a gold pass, the secod oe a silve pass ad the thid oe a boze pass. I how may diffeet ways ca the passes be give out? Ay of the 15 people ca eceive the fist pass. Thee ae 14 people left who could eceive the secod pass. Similaly thee ae 13 people that could eceive the thid pass. Total umbe of possibilities 15# 14# I Lotto, a machie cotais 45 balls, each with a diffeet umbe fom 1 to 45. (a) I how may ways ca 6 balls be adomly daw? (b) To wi fist pize i Lotto, a peso must choose all 6 umbes coectly. Lisa has 3 tickets i the same daw of Lotto. What is the pobability that she will wi fist pize? (a) The fist ball could be ay of the 45 balls. The secod could be ay of the emaiig 44 balls ad so o. The umbe of ways 45# 44# 43# 42# 41# (b) P ^fist pize h Execises 1. A passwod has 4 lettes. How may combiatios ae possible? 2. A motocycle umbeplate is made up of 2 lettes followed by 2 umbes. How may umbeplates of this type ae available? 3. A passwod ca have up to 5 lettes followed by 4 umbes o it. If I could use ay lette of the alphabet o umbe, how may diffeet passwods could be fomed? Leave you aswe i idex fom.
10 Chapte 13 Pemutatios ad Combiatios A witess saw most of the umbeplate o a getaway ca except fo the fist lette ad the last umbe. How may diffeet cas do the police eed to check i ode to fid this ca? 5. A cetai bad of compute has a seial umbe made up of 10 lettes the 15 umbes. How may computes with this type of seial umbe ca be made? Leave you aswe i idex fom. 6. Victoia has postcodes statig with 3. How may diffeet postcodes ae available i Victoia? 7. A couty tow has telephoe umbes statig with 63 followed by ay 6 othe umbes fom 0 to 9. How may telephoe umbes ae possible i this tow? 8. Yasmi has 12 tops, 5 pais of jeas ad 5 pais of shoes i he wadobe. If she adomly chooses a top, pai of jeas ad shoes, how may combiatios ae possible? 9. A ca maufactue poduces cas i 8 diffeet colous, with eithe maual o automatic gea tasmissio, ad 4 diffeet types of wheels. How may diffeet combiatios ca it poduce? 10. A PIN has 4 umbes. If I foget my PIN I am allowed 3 ties to get it ight. Fid the pobability that I get it withi the 3 ties. 11. A estauat offes 7 mai couses ad 4 dessets, as well as 3 diffeet types of coffee. (a) How may diffeet combiatios of mai couse, desset ad coffee ae possible? (b) Fid the pobability that I adomly pick the combiatio voted most favouite. 12. A telephoe umbe i a capital city ca stat with a 9 ad has 8 digits altogethe. (a) How may telephoe umbes ae possible? (b) If I foget the last 3 digits of my fied s telephoe umbe, how may umbes would I have to ty fo the coect umbe? 13. A compay maufactues compute chips. If it uses a seial umbe o each oe cosistig of 10 lettes, will thee be eough combiatios fo all these chips? 14. A passwod cosists of 2 lettes followed by 5 umbes. What is the pobability that I adomly guess the coect passwod? 15. A city has a populatio of How may digits should its telephoe umbes have so that evey peso ca have oe? 16. A maufactue of compute pats puts a seial umbe o each pat, cosistig of 3 lettes, 4 umbes the 4 lettes. The umbe of pats sold is estimated as 5 millio. Will thee be eough combiatios o this seial umbe to cope with these sales? 17. A bidal shop caies 12 diffeet types of bidal desses, 18 types of veils ad 24 diffeet types of shoes. If Kate chooses a combiatio of dess, veil ad
11 726 Maths I Focus Mathematics Extesio 1 Pelimiay Couse shoes at adom, what is the pobability that she chooses the same combiatio as he fied Jae? 18. Kate chooses a diffeet coloued dess fo each of he 3 bidesmaids. If the colous ae adomly give to each bidesmaid, how may diffeet possibilities ae thee? 3 fee haicuts adomly give away, i how may ways could this be doe? 23. A flock of 28 pelicas is fed 6 fish cacasses. If each cacass is give to a diffeet pelica, i how may ways ca this happe? 19. I a compute ca ace game, the cas that come fist, secod ad thid ae adomly awaded. If thee ae 20 cas, how may possible combiatios of fist, secod ad thid ae thee? 20. Jacquie oly has 4 chocolates left ad decides to adomly choose which of he 6 fieds will eceive oe each. How may possible ways ae thee i which ca she give the chocolates away? 21. Thee pizes ae give away at a cocet by tapig them udeeath adom seats. If thee ae 200 people i the audiece, i how may ways ca these pizes be wo? 22. Thee ae 7 cliets at a haidessig salo. If thee ae 24. A set of cads is umbeed 1 to 100 ad 2 chose at adom. (a) How may diffeet aagemets of odeed pais ae possible? (b) What is the pobability that a paticula odeed pai is chose? 25. Each of 10 cads has a lette witte o it fom A to J. If 3 cads ae selected i ode at adom, fid the pobability that they spell out CAB. Factoial otatio Coutig outcomes whe epetitio o eplacemet is allowed is quite staightfowad, eve whe the umbes become vey lage. EXAMPLE A cad is daw adomly fom a set of 25 cads umbeed 1 to 25 i tu ad the eplaced befoe the ext is selected. How may possible outcomes ae thee if 25 cads ae chose this way? Aswe i scietific otatio, coect to 3 sigificat figues.
12 Chapte 13 Pemutatios ad Combiatios 727 Each time thee is a cad daw, thee ae 25 possibilities. Total umbe 25# 25# 25#...# 25 ] 25 timesg # Whe thee is o epetitio o eplacemet, the calculatios ca be quite log. EXAMPLE A cad is daw adomly fom a set of 25 cads umbeed 1 to 25 i tu without eplacig it befoe the ext is daw. How may possible outcomes ae thee if all 25 cads ae daw out? Aswe i scietific otatio, coect to 3 sigificat figues. Fist cad: thee ae 25 possibilities. Secod cad: thee ae oly 24 possibilities sice oe cad has aleady bee daw out. Thid cad: thee ae 23 possibilities ad so o. Total umbe 25# 24# 23# # 3# 2# # This calculatio is quite tedious! Factoial otatio allows us to easily calculate the umbe of possible outcomes whe selectig all objects i ode with o eplacemet o epetitio.! ] - 1g] - 2g] - 3g] - 4g... 3# 2# 1 You ca fid a x! key o most scietific calculatos. Sice the sequece of umbes multiplied does t go futhe tha 1, the by covetio we say that 0! 1 Check 0! o you calculato.
13 728 Maths I Focus Mathematics Extesio 1 Pelimiay Couse EXAMPLES 1. Evaluate (a) 4! (b) 7! (c) 25! (aswe i scietific otatio coect to 3 sigificat figues.) (a) 4! # # # It is much easie to use the x! key o a calculato to fid this. (b) 7! 7 # 6 # 5# 4 # 3# 2 # (c) 25! 1. 55# A goup of 9 teeages is waitig to be seved i a café. They ae each adomly assiged a umbe fom 1 to 9. (a) I how may ways is it possible fo the umbes to be assiged? (b) Oe of the goup eeds to be seved quickly as he has to leave. If he is give the fist umbe, i how may ways is it possible fo the umbes to be assiged? (a) The fist umbe could be assiged 9 ways. The secod umbe could be assiged 8 ways ad so o. Total ways 9! (b) Oe of the goup is give the fist ticket (this ca oly happe i oe way) The secod umbe could be assiged 8 ways ad so o. Total ways 1# 8! Execises 1. Evaluate (a) 6! (b) 10! (c) 0! (d) 8! - 7! (e) 5# 4! 7! (f) 4! 12! (g) 5! 13! (h) 4!9! 8! (i) 3!5! 11! (j) 4!7!
14 Chapte 13 Pemutatios ad Combiatios A goup of 9 jockeys ae each give a set of idig colous to wea. If these ae give out i ode adomly, how may diffeet aagemets ae possible? 8. A goup of 7 people lie up to do kaaoke. If they ae each adomly give a sog to sig, how may possible outcomes ae thee? 9. A kidegate class has a abbit, a mouse ad a paot. Thee childe ae selected to take these pets home fo the holidays. If the pets ae adomly give out to these childe, how may diffeet ways ae possible? 10. A PIN cosists of 6 umbes, with o epetitio of ay umbes allowed. How may diffeet PINs ae possible? 3. Each of 6 people at a estauat is give a diffeet coloued glass. How may possible combiatios ae thee? 4. A moutai tail oly has oom fo oe peso at a time. If 12 people ae waitig at the bottom of the tail ad ae adomly picked to stat out, i how may ways ca this happe? 5. A dog walke has 5 dogs ad 5 leashes. I how may diffeet ways is it possible to put a leash o each dog? 6. Thee ae 11 people i a choi ad each eceives a musical scoe. (a) I how may diffeet ways could the scoes be haded out? (b) Russell, the musical diecto, also eeds a musical scoe. I how may ways could the scoes be haded out fo the choi ad the musical diecto? 7. A ow of seats i a theate seats 8 people. I how may ways could a goup of 8 fieds be adomly seated i this ow? 11. I a chous fo a school musical, 7 studets each wea a diffeet mask. I how may diffeet ways ca the masks be wo by these studets? 12. If 15 people play a game of Kelly pool, each peso i tu chooses a umbe at adom betwee 1 ad 15. I how may diffeet ways ca this occu? Aswe i scietific otatio, coect to oe decimal place. 13. (a) A school talet quest has 11 pefomes ad each oe is adomly give the ode i which to pefom. I how may ways ca the ode of pefomaces be aaged? (b) If oe pefome is chose to pefom fist, i how may ways ca the othes be aaged? 14. A goup of 6 fieds sit i the same ow at a cocet. (a) I how may diffeet ways ca they aage themselves? (b) If oe fied must sit o the aisle, i how may ways ca they be aaged?
15 730 Maths I Focus Mathematics Extesio 1 Pelimiay Couse 15. A goup of 8 fieds go to a estauat ad sit at a oud table. If the fist peso ca sit aywhee, i how may ways ca the othes be aaged aoud the table? 16. I a pack of cads, the 4 aces ae take out ad shuffled. (a) What is the pobability of pickig out the Ace of Heats at adom? (b) If all the aces ae aaged i ode, what is the pobability of guessig the coect ode? 17. At a weddig, each of the 12 tables is to have a cetepiece with a diffeet coloued ose. (a) I how may diffeet ways ca the oses be aaged at adom? (b) What is the pobability that the bide will have a pik ose at he table? 18. I a maths exam, a studet has to aage 5 decimals i the coect ode. If he has o idea how to do this ad aages them adomly, what is the pobability that he makes the ight guess fo all the decimals? 19. I a ca ace, the fastest ca is give pole positio ad the othe cas ae adomly give thei statig positios. If thee ae 14 cas altogethe, i how may ways ca this be aaged? 20. Show that 8! (a) 8# 7# 6# 5 4! (b) (c) 11! 6!!! 11# 10# 9# 8# 7 ] - 1g] - 2g] - 3g...] + 1g whee 2! (d) ( - )! ] - 1g] - 2g] - 3g...] - + 1g whee 2 Pemutatios Factoial otatio is useful fo fidig the umbe of possible outcomes whe aagig all objects i ode without eplacemet. Howeve, sometimes we eed to fid the umbe of possible outcomes whe aagig oly some of the objects i ode without eplacemet. It is easy to aage objects with eplacemet.
16 Chapte 13 Pemutatios ad Combiatios 731 EXAMPLE I how may ways ca 5 cads be selected fom a total of 20 cads if each oe is eplaced befoe selectig the ext oe? Each selectio ca be made i 20 possible ways. Total 20# 20# 20# 20# ways. Fo selectios fom objects (with epetitios), the umbe of possible outcomes is # # # f ( times) o Howeve, whe aagig objects fom objects i ode without eplacemet, it is ot so easy. EXAMPLE I how may ways ca 5 cads be selected fom a total of 20 cads if thee is o eplacemet? The 1 st cad ca be selected i 20 diffeet ways. The 2 d cad ca be selected i 19 diffeet ways as the fist cad is o loge beig used. The 3 d cad ca be selected i 18 diffeet ways, ad so o. Total 20# 19# 18# 17# ways The calculatios ca become tedious if we select a lage umbe of objects.
17 732 Maths I Focus Mathematics Extesio 1 Pelimiay Couse EXAMPLE If thee ae 20 cads ad 13 cads ae chose i ode at adom without eplacemet, fid the possible umbe of ways the cads ca be chose i scietific otatio coect to 1 decimal place. The fist cad ca be ay of the 20 umbes. The secod cad ca be ay of the emaiig 19 umbes. The thid ca be ay of the emaiig 18 umbes. The umbe of ways the cads ca be chose 20# 19# 18# 17# f# # 10 Fo odeed selectios fom objects without eplacemet, the umbe of possible outcomes is # ] -1g#] -2g#] -3g f ] timesg o ] -1g] - 2g] - 3g f ] - + 1g A pemutatio descibes a aagemet of objects fom a total of objects i a cetai ode without eplacemet o epetitio. You ca fid a P key o most scietific calculatos. Pemutatio P is the umbe of ways of makig odeed selectios of objects fom a total of objects.! P ] - g! Poof P ] -1g] - 2g] - 3g f ] - + 1g ] - g] - -1g] - - 2gf 3 $ 2 $ 1 ] -1g] - 2g] - 3g f ] - + 1g # ] - g] - -1g] - - 2gf 3 $ 2 $ 1 ] -1g] - 2g] - 3g f] - + 1g] - g] - -1g] - - 2gf3 $ 2 $ 1 ] - g] - -1g] - - 2gf 3 $ 2 $ 1! ] - g! A special case of this esult is: P!
18 Chapte 13 Pemutatios ad Combiatios 733 Poof `! P ] - g!! P ] - g!! 0!! 1! EXAMPLES 1. Evaluate 9 P4 You ca evaluate this o a calculato. 9 9! P 4 ] 9-4g! 9! 5! 9 $ 8 $ 7 $ 6 $ 5 $ 4 $ 3 $ 2 $ 1 5 $ 4 $ 3 $ 2 $ 1 9 $ 8 $ 7 $ (a) Fid the umbe of aagemets of 3 digits that ca be fomed usig the digits 0 to 9 if each digit ca oly be used oce. (b) How may 3 digit umbes geate tha 700 ca be fomed? (a) Thee ae 10 digits fom 0 to 9. The 1 st digit ca be ay of the 10 digits. The 2 d digit ca be ay of the emaiig 9 digits. The 3 d digit ca be ay of the emaiig 8 digits. Total pemutatios 10# 9# ! o 10 P 3 ] 10-3g! 10! 7! 720 CONTINUED
19 734 Maths I Focus Mathematics Extesio 1 Pelimiay Couse (b) The 1 st digit must be 7 o 8 o 9 (3 possible digits). The 2 d digit ca be ay of the emaiig 9 digits. The 3 d digit ca be ay of the emaiig 8 digits. Total aagemets 3# 9# Aothe method: Thee ae 3 ways to get the 1 st digit. The possible aagemets of the emaiig 2 digits is 9 P2 9 Total aagemets 3# P2 3# Thee ae some special examples that eed vey caeful coutig, such as aagemets aoud a cicle. Othes ivolve coutig whe thee ae idetical objects. EXAMPLES 1. (a) I how may ways ca 6 people sit aoud a cicula table? (b) If seatig is adom, fid the pobability that 3 paticula people will sit togethe. (a) The 1 st peso ca sit aywhee aoud the table so we oly eed to aage the othe 5 people. The 2 d peso ca sit i ay of the 5 emaiig seats. The 3 d peso ca sit i ay of the emaiig 4 seats ad so o. Total aagemets 5! 120
20 Chapte 13 Pemutatios ad Combiatios 735 (b) The 3 people ca sit aywhee aoud the table togethe i 3# 2# 1 o 3! ways. The emaiig 3 people ca sit togethe i 3! ways. Total aagemets 3! # 3! P ( 3 sit togethe ) I how may ways ca the lettes of the wod EXCEPTIONAL be aaged? EXCEPTIONAL has 11 lettes with the lette E epeated. If each E was diffeet, i.e. E 1 ad E 2, the thee would be 11! aagemets. Howeve, we caot tell the diffeece betwee the 2 Es. Sice thee ae 2! ways of aagig the Es, the thee ae 2! aagemets of the wod EXCEPTIONAL that ae idetical. We eed to divide by 2! to elimiate these idetical aagemets. 11! Total aagemets 2! The umbe of diffeet ways of aagig objects i which a of the objects ae of oe kid, b objects ae of aothe! kid, c of aothe kid ad so o, is give by abc!!! f whee a + b + c + f # EXAMPLE Fid the umbe of ways that the wod ANAETHEMA ca be aaged. Thee ae 9 lettes, icludig 3 As ad 2 Es. Thee ae 9! ways of aagig the lettes, with 3! ways of aagig the As ad 2! ways of aagig the Es. 9! Total aagemets 32!!
21 736 Maths I Focus Mathematics Extesio 1 Pelimiay Couse Some questios ivolvig coutig eed diffeet appoaches ad sometimes it is just a matte of logically wokig it out. EXAMPLES A bag cotais 5 balls of diffeet colous ed, yellow, blue, gee ad white. I how may ways ca these 5 balls be aaged (a) with o estictios (b) if the yellow ball must be fist (c) if the fist ball must ot be ed o white (d) if blue ad gee must be togethe (e) if ed, blue ad gee must be togethe? (a) The 1 st ca be ay of the 5 balls. The 2 d ca be ay of the emaiig 4 balls ad so o. Total aagemets 5! 120 (b) The 1 st ball must be yellow, so thee is oly 1 way of aagig this. The 2 d ball ca be ay of the emaiig 4 balls. The 3 d ball ca be ay of the emaiig 3 balls ad so o. Total aagemets 4! 24 (c) The 1st ball could be yellow, blue o gee so thee ae 3 possible aagemets. The 2 d ball could be ay of the emaiig 4 balls ad so o. Total aagemets 3# 4! 72 (d) Whe two objects must be togethe, we teat them as a sigle object with 2! possible aagemets. So we aage 4 balls i 4! ways: R, Y, BG ad W. But thee ae 2! ways i which to aage the blue ad gee balls. Total aagemets 4! # 2! 48 (e) Whe thee objects ae togethe, we teat them as a sigle object with 3! possible aagemets. We ae the aagig 3 balls i 3! ways: RBG, Y, W. But thee ae 3! ways i which to aage the ed, blue ad gee balls. Total aagemets 3! # 3! 36
22 Chapte 13 Pemutatios ad Combiatios Execises 1. Wite each pemutatio i factoial otatio ad the evaluate. (a) P 6 3 (b) 5 P2 (c) 8 P3 (d) 10 P7 (e) 9 P6 (f) 7 P5 (g) 8 P6 (h) (i) (j) 11 P8 9 P1 6 P6 2. A set of 26 cads, each with a diffeet lette of the alphabet, is placed ito a hat ad cads daw out at adom. Fid the umbe of wods possible if selectig (a) 2 cads (b) 3 cads (c) 4 cads (d) 5 cads. 3. A 3 digit umbe is adomly made fom cads cotaiig the umbes 0 to 9. (a) I how may ways ca this be doe if the cads caot be used moe tha oce ad zeo caot be the fist umbe? (b) How may umbes ove 400 ca be made? (c) How may umbes less tha 300 ca be made? 4. A set of 5 cads, each with a umbe fom 1 to 5 o it, is placed i a box ad 2 daw out at adom. Fid the possible umbe of combiatios (a) altogethe (b) of umbes geate tha 50 possible (c) of odd umbes (d) of eve umbes. 5. (a) How may aagemets of the lettes A, B, C ad D ae possible if o lette ca be used twice? (b) How may aagemets of ay 3 of these lettes ae possible? 6. A 4 digit umbe is to be selected at adom fom the umbes 0 to 9 with o epetitio of digits. (a) How may aagemets ca thee be? (b) How may aagemets of umbes ove 6000 ae thee? (c) How may aagemets of umbes less tha 8000 ae thee? 7. The umbes 1, 2, 3, 4 ad 5 ae aaged i a lie. How may aagemets ae possible if (a) thee is o estictio (b) the umbe is less tha (c) the umbe is geate tha (d) the umbe is odd (e) ay 3 umbes ae selected at adom? 8. Thee ae 12 swimmes i a ace. (a) I how may ways could they fiish? (b) I how may ways could they come i fist, secod ad thid? 9. How may diffeet odeed aagemets ca be made fom the wod COMPUTER with (a) 2 lettes (b) 3 lettes (c) 4 lettes? The fist umbe caot be zeo. The fist umbe is ot zeo.
23 738 Maths I Focus Mathematics Extesio 1 Pelimiay Couse All beads ae diffeet fom each othe. 10. How may diffeet odeed aagemets ca be made fom these wods? (a) CENTIPEDE (b) ALGEBRA (c) TELEVISION (d) ANTARCTICA (e) DONOR (f) BASKETBALL (g) GREEDY (h) DUTIFUL (i) MANUFACTURER (j) AEROPLANE 11. A goup of fieds queue outside a estauat i a staight lie. Fid how may ways the fieds ca be aaged if thee ae (a) 4 fieds (b) 7 fieds (c) 8 fieds (d) 10 fieds (e) 11 fieds. 12. A goup of fieds go ito a estauat ad ae seated aoud a cicula table. Fid how may aagemets ae possible if thee ae (a) 4 fieds (b) 7 fieds (c) 8 fieds (d) 10 fieds (e) 11 fieds. 13. A stig of beads looks the same if tued ove. Fid the umbe of diffeet aagemets possible with (a) 10 beads (b) 12 beads (c) 9 beads (d) 11 beads (e) 13 beads. 14. I how may ways ca a goup of 6 people be aaged (a) i a lie (b) i a cicle? 15. Fid how may diffeet ways a goup of 9 people ca be aaged i (a) a lie (b) a cicle. 16. I how may ways ca a set of 10 beads be aaged (a) i a lie (b) i a cicle aoud the edge of a poste (c) o a bacelet? 17. (a) How may diffeet aagemets ca be made fom the playig cads Jack, Quee, Kig ad Ace? (b) If I choose 2 of these cads adomly, how may diffeet aagemets could I make? (c) If I choose 3 of these cads adomly, how may diffeet aagemets could I make? 18. A goup of 7 people sit aoud a table. I how may ways ca they be aaged (a) with o estictios (b) if 2 people wat to sit togethe (c) if 2 people caot sit togethe (d) if 3 people sit togethe? 19. A goup of 5 boys ad 5 gils lie up outside a ciema. I how may ways ca they be aaged (a) with o estictio? (b) If a paticula gil stads i lie fist? (c) If they alteate betwee boys ad gils (with eithe a gil o boy i fist place)? 20. Fid the pobability that if 10 people sit aoud a table, 2 paticula people will be seated togethe at adom.
24 Chapte 13 Pemutatios ad Combiatios A bookshelf is to hold 5 mathematics books, 8 ovels ad 7 cookbooks. (a) I how may diffeet ways could they be aaged? (Leave aswe i factoial otatio.) (b) If the books ae gouped i categoies, i how may ways ca they be aaged? (Aswe i factoial otatio.) (c) If oe book is chose at adom, fid the pobability that it is a cookbook. 22. (a) How may diffeet aagemets ca be made fom the umbes 3, 4, 4, 5 ad 6? (b) How may aagemets fom umbes geate tha 4000? (c) How may fom umbes less tha 5000? (d) If a aagemet is made at adom, fid the pobability that it is less tha Fid the pobability that a aagemet of the wod LAPTOP will stat with T. 24. What is the pobability that if a 3 lette wod is fomed adomly fom the lettes of PHYSICAL, it will be CAL? 25. A mibus has 6 fowad facig ad 2 backwad facig seats. If 8 people use the bus, i how may ways ca they be seated (a) with o estictios (b) if oe peso must sit i a fowad facig seat (c) if 2 people must sit i a fowad facig seat? 26. If 3 lettes of the wod VALUED ae selected at adom, fid the umbe of possible aagemets if (a) the fist lette is D. (b) the fist lette is a vowel. 27. The lettes of the wod THEORY ae aaged adomly. Fid the umbe of aagemets. (a) with o estictios. (b) if the E is at the begiig. (c) if the fist lette is a cosoat ad the last lette is a vowel. 28. Fid the umbe of aagemets possible if x people ae (a) i a staight lie (b) i a cicle (c) i a cicle with 2 people togethe (d) i a staight lie with 3 people togethe (e) i a cicle with 2 people ot togethe. 29. (a) Use factoial otatio to 8 8 P P 3 5 show that 3! 5! P P - (b) Pove that! ] - g! Pove that P P + P - 1 Vowels ae lettes a, e, i, o ad u while cosoats ae all othe lettes.
25 740 Maths I Focus Mathematics Extesio 1 Pelimiay Couse Combiatios The pemutatio P is the umbe of aagemets possible fo a odeed selectio of objects fom a total of objects. Whe the ode is ot impotat, fo example whe AB is the same as BA, the umbe of aagemets is called a combiatio. EXAMPLES 1. A committee of 2 is chose fom Scott, Rachel ad Kate. I how may ways ca this be doe? 3 Numbe of odeed aagemets P2 6 Howeve, a committee of Scott ad Rachel is the same as a committee of Rachel ad Scott. This is the same fo all othe aagemets of the committee. Thee ae 2! ways of aagig each committee of two people. To get the umbe of uodeed aagemets, we divide the umbe of odeed aagemets by 2! 3 P2 Total aagemets 2! 3 2. Thee ae 3 vacacies o a school coucil ad 8 people who ae available. If the vacacies ae filled adomly, i how may ways ca this happe? 8 Numbe of odeedaagemets P3 Howeve, ode is ot ecessay hee, sice the 3 vacacies filled by, say, Hamish, Amie ad Macus, would be the same i ay ode. Thee ae 3! diffeet ways of aagig Hamish, Amie ad Macus. 8 P3 So total aagemets 3! 56 The umbe of ways of makig uodeed selectios of P! objects fom is which is the same as! ] - g!!
26 Chapte 13 Pemutatios ad Combiatios 741 Poof P is the odeed selectio of objects fom objects. Thee ae! ways of aagig objects. If ode is uimpotat, the uodeed selectio of objects fom is give P by!.! P ] - g!!!! 1 # ] - g!!! ] - g!! Combiatio C o a k is the umbe of ways of makig uodeed selectios of objects fom a total of objects.! C ] -! g! We ca call this choose otatio. EXAMPLES 1. A bag cotais 3 white ad 2 black coutes labelled W 1, W 2, W 3 ad B 1, B 2. If two coutes ae daw out of the bag, i how may ways ca this happe if ode is ot impotat? Possible aagemets (uodeed) ae: WW WW WB BB WW WB WB WB WB WB 1 2 Thee ae 10 diffeet combiatios. Usig combiatios, the umbe of diffeet aagemets of choosig 2 coutes fom 5 is 5 C ! C 2 (5-2)!2! 5! 3!2! 10 CONTINUED
27 742 Maths I Focus Mathematics Extesio 1 Pelimiay Couse 2. If 12 cois ae tossed, fid the umbe of ways of tossig 7 tails. The ode is ot impotat. 12 Thee ae C ways of tossig 7 tails fom 12 cois ! C 7 (12-7)!7! 12! 5!7! (a) A committee of 5 people is fomed adomly fom a goup of 15 studets. I how may diffeet ways ca the committee be fomed? (b) If the goup cosists of 9 seio ad 6 juio studets, i how may ways ca the committee be fomed if it is to have 3 seio ad 2 juio studets i it? (a) The ode of the committee is ot impotat. Numbe of aagemets b15l (b) 3 seio studets ca be chose i b9l 3 o 84 ways. 2 juio studets ca be chose i b6 2 l o 15 ways. 9 6 Total umbe of aagemets c m# c m # A team of 6 me ad 5 wome is chose at adom fom a goup of 10 me ad 9 wome. If Kaye ad Geg both hope to be chose i the team, fid the pobability that (a) both will be chose (b) eithe will be chose The umbe of possible teams C # C # (a) Fo Kaye to be chose, the 4 out of the othe 8 wome will be chose i.e. 8 C4 Fo Geg to be chose, 5 out of the othe 9 me will be chose i.e. 9 C5
28 Chapte 13 Pemutatios ad Combiatios 743 Numbe of combiatios Pobability 8 9 C # C # (b) Fo Kaye ad Geg ot to be icluded, the 5 out of the othe 8 wome ad 6 out of the othe 9 me will be chose. 8 9 Numbe of combiatios C # C # Pobability Execises 1. Wite i factoial otatio ad evaluate. (a) b9l 5 (b) b 12 l 7 (c) b8l 3 (d) (e) 10 C4 11 C5 2. (a) Evaluate (i) (ii) (iii) (iv) 10 C0 7 C b 9 C9 11 (v) c m 11 (b) Hece complete (i) C 0 (ii) l C 3. Fid the umbe of diffeet ways that a committee of 6 people ca be made adomly fom a goup of (a) 8 people (b) 9 people (c) 11 people (d) 15 people (e) 20 people. 4. (a) A set of 3 ed cads ad 3 blue cads ae placed i a box. By amig the ed cads R 1, R 2 ad R 3 ad the blue cads B 1, B 2 ad B 3, list the umbe of diffeet aagemets possible whe 2 cads ae daw out at adom, with ode ot impotat. How may aagemets ae possible? (b) If thee ae 10 ed ad 10 blue cads ad 7 ae daw out at adom, how may diffeet combiatios ae possible? 5. A coi is tossed 20 times. How may diffeet aagemets ae thee fo tossig 5 heads? The cads ae all distict fom each othe.
29 744 Maths I Focus Mathematics Extesio 1 Pelimiay Couse 6. A set of 10 mables ae placed i a bag ad 6 selected at adom. I how may diffeet ways ca this happe? 7. I poke, 5 cads ae dealt fom a pack of 52 playig cads. How may diffeet aagemets ae possible? 8. Thee cads ae daw adomly fom a set of 10 cads with the umbes 0 to 9 o them. How may diffeet aagemets ae possible if ode is (a) impotat (b) uimpotat? 9. A debatig team of 3 is chose fom a class of 14 studets. I how may ways ca the team be selected if ode is (a) impotat (b) uimpotat? 10. A bag cotais 12 diffeet lollies with blue wappes ad 15 diffeet lollies with ed wappes. If I take 6 lollies out of the bag, how may diffeet combiatios ae possible? 11. A team of 4 playes is chose at adom fom a goup of 20 teis playes to play a exhibitio match. I how may ways could the team be chose? 12. A goup of 3 studets to go o a studet epesetative coucil is chose at adom fom a class of 27. I how may diffeet ways could this be doe? 13. A boad of 8 people is chose fom a membeship of 35. How may diffeet combiatios ae possible? 14. A basketball team of 5 playes is selected at adom fom a goup of 12 PE studets. (a) I how may ways ca the team be selected? (b) Fid the pobability that Eik is selected as oe of the team membes. (c) Fid the pobability that Eik ad Jes ae both selected. 15. A committee of 6 people is to be selected adomly fom a goup of 11 me ad 12 wome. Fid the umbe of possible committees if (a) thee is o estictio o who is o the committee (b) all committee membes ae to be male (c) all membes ae to be female (d) thee ae to be 3 me ad 3 wome (e) a paticula woma is icluded (f) a paticula ma is ot icluded (g) thee ae to be 4 wome ad 2 me. 16. A hose ace has 15 hoses competig ad at the TAB, a quiella pays out o the hoses that come i fist ad secod, i eithe ode. Rya decides to bet o all possible combiatios of quiellas. If it costs him $1 a bet, how much does he pay? 17. A goup of 25 studets cosist of 11 who play a musical istumet ad 14 who do t. Fid the umbe of diffeet aagemets possible if a goup of 9 studets is selected at adom (a) with o estictio (b) who all play musical istumets (c) whee 5 play musical istumets (d) whee 2 do t play musical istumets.
30 Chapte 13 Pemutatios ad Combiatios A set of cads cosists of 8 yellow ad 7 ed cads. (a) If 10 cads ae selected at adom, fid the umbe of diffeet aagemets possible. (b) If 8 cads ae selected, fid the umbe of aagemets of selectig (i) 4 yellow cads (ii) 6 yellow cads (iii) 7 yellow cads (iv) 5 ed cads. 19. Te cads ae selected adomly fom a set of 52 playig cads. Fid the umbe of combiatios selected if (a) thee ae o estictios (aswe i scietific otatio coect to 3 sigificat figues) (b) they ae all heats (c) thee ae 7 heats (d) they ae all ed cads (e) thee ae 4 aces. 20. A aimal efuge has 17 dogs ad 21 cats. If a usig home odes 12 aimals at adom, fid the umbe of ways that the ode would have (a) 7 dogs (b) 9 dogs (c) 10 dogs (d) 4 cats (e) 6 cats. 21. Thee ae 8 white, 9 ed ad 5 blue mables i a bag ad 7 ae daw out at adom. Fid the umbe of aagemets possible (a) with o estictio (b) if all mables ae ed (c) if thee ae 3 white ad 2 ed mables (d) if thee ae 4 ed ad 1 blue mables (e) if thee ae 4 white ad 2 blue mables. 22. Out of a goup of 25 studets, 7 walk to school, 12 catch a tai ad 6 catch a bus. If 6 studets ae selected, fid the umbe of combiatios if (a) all walk to school (b) oe catch a bus (c) 3 walk to school ad 1 catches a bus (d) 1 walks to school ad 4 catch a tai (e) 3 catch a tai ad 1 catches a bus. 23. At a kaaoke ight, a goup of 14 fieds decide that 4 of them will sig a sog togethe. Of the fieds, 5 have peviously sug this sog befoe. I how may ways ca they do this if they select (a) fieds who have all sug the sog peviously (b) 2 of the fieds who sag the sog peviously (c) oe of the fieds who sag the sog peviously? (a) Evaluate C5 12 (b) Evaluate C7 (c) By usig factoial otatio, show why C C 25. By evaluatig both sides, show that C C + C Show that a13k a13k Show that b 10 l b 9 l b l Pove that b l b l Pove that P! C Pove that b l b - 1 k - l 1 + b - 1 l k k 5 7 The cads ae all distict fom each othe. All mables ae distict.
31 746 Maths I Focus Mathematics Extesio 1 Pelimiay Couse Test youself Fid the umbe of ways of aagig 7 people (a) i a staight lie (b) i a cicle. 2. A bag cotais 8 ed, 5 gee ad 9 yellow mables. If a mable is chose at adom, fid the pobability that it is (a) ed (b) gee o ed (c) ot gee. 3. A caiage has 2 seats facig fowads ad 2 seats facig backwads. Fid the umbe of ways of seatig 4 people i the caiage if (a) thee ae o estictios (b) oe peso must sit facig fowads. 4. A set of 10 cads, umbeed 1 to 10, is placed ito a box ad 3 daw out at adom. Fid the umbe of aagemets possible if ode is (a) impotat (b) uimpotat. 5. A goup of 10 boys ad 16 gils ae o a school excusio. Five of them ae chose at adom to help the teache check the olls. Fid the umbe of ways these studets could be selected if (a) thee is o estictio (b) 3 ae gils (c) all ae boys. 6. The pobability of wiig a game of chace is 59% ad the pobability of a daw is 12%. What is the pobability of losig? 7. I how may ways ca 3 lette wods be selected at adom fom the wod RANDOM? 8. A set of cads umbeed fom 1 to 20 is aaged adomly. I how may ways ca this be doe? (Aswe i scietific otatio, to 2 sigificat figues.) 9. The pobability of a missile hittig a taget is 9 8. What is the pobability of the missile missig the taget? 10. A 5 peso committee is selected fom a class of 30 studets. I how may ways ca the committee be selected? 11. I a hose ace, a peso bets at the TAB o a tifecta. To wi, the peso must pick the fist 3 hoses i ode. I how may ways is it possible to wi if thee ae 11 hoses i the ace? 12. (a) A goup of 9 fieds go out to die ad sit at a oud table. I how may ways ca this be doe? (b) The 9 fieds the go to a ightclub ad adomly queue up to get i. How may aagemets ae thee? (c) If Jack ad Jill queue up togethe, i how may ways ca the fieds lie up? (d) Oce they get ito the ightclub, thee is oly a table fo 3 available, ad the othes will have to stad up. If the fieds adomly assig who sits at the table, i how may diffeet ways ca they be seated? 13. How may diffeet aagemets ae thee of the wod (a) PERMUTATION (b) COMBINATION (c) FACTORIAL (d) PROBABILITY (e) SELECTION
32 Chapte 13 Pemutatios ad Combiatios A set of cois ae tossed. Fid the umbe of ways if tossig k tails. 15. A set of 20 cads is umbeed 1 to 20 ad 6 selected at adom. Fid the umbe of aagemets of selectig (a) all odd umbes (b) the last 2 umbes less tha I Austalia Idyll, thee ae 12 siges who must choose a sog to sig fom a list of 32 sogs. Each sige takes tus i ode to adomly choose a sog. I how may ways could these choices be made? Aswe i scietific otatio coect to 2 decimal places. 17. A ballet class has 30 studets i it. Of these studets, 21 ae pactisig fo a ballet exam. If 8 studets ae chose at adom, fid the umbe of ways that (a) 5 ae pactisig fo the exam (b) all ae pactisig fo the exam (c) 3 ae pactisig fo the exam. 18. Evaluate (a) a6k 4 (b) 9 P7 19. A seial umbe is made up of 4 lettes ad 2 umbes. If zeo is ot allowed, fid how may seial umbes ae possible. 20. (a) Evaluate 0! (b) Show that a k a k 0 Challege Execise Numbes ae fomed fom the digits 1, 2, 3, 3, ad 7 at adom. (a) I how may ways ca they be aaged with o estictios? (b) I how may ways ca they be aaged to fom a umbe geate tha ? 2. A cham bacelet has 6 chams o it. I how may ways ca the chams be aaged if the bacelet (a) has a clasp (b) has o clasp? 3. Show that b l k b l k b l k fo 1# k # A goup of people sit aoud a cicula table. (a) I how may ways ca they be aaged? (b) How may aagemets ae possible if k people sit togethe? 5. (a) How may diffeet aagemets of the wod CHALLENGE ae thee? (b) How may diffeet aagemets ae possible if 3 lettes ae adomly selected fom the wod CHALLENGE ad aaged ito wods? 6. A subcommittee of 5 people is fomed fom the 12 membes of a boad. (a) If this is a adom selectio, i how may diffeet ways ca the committee be fomed? (b) If thee ae 4 NSW membes ad 3 Queeslad membes o the boad, what is the pobability that 2 NSW ad 2 Queeslad membes will be o the committee?
33 748 Maths I Focus Mathematics Extesio 1 Pelimiay Couse 7. Pove that P! C 8. A maagemet committee is made up of 5 athletes ad 3 maages. If the committee is fomed adomly fom a goup of 20 athletes ad 10 maages, fid (a) the umbe of diffeet ways i which the committee could be fomed (b) the pobability that Macus, a athlete, is icluded (c) the pobability that both Macus ad his gilfied, Rachel who is a maage, ae icluded (d) the pobability that Macus ad Rachel ae excluded fom the committee. out at adom i ode. Fid the umbe of diffeet possible aagemets if (a) thee is o estictio (b) all the umbes ae 90 o moe (c) all umbes ae eve (d) all umbes ae less tha 20 (e) the fist umbe is geate tha 60 (f) the fist 2 umbes ae odd. 10. I a goup of 35 studets, 18 play socce ad 21 play basketball. All studets play at least oe of these spots. If oe of these studets is selected at adom, fid the pobability that this studet (a) plays both socce ad basketball (b) plays basketball but ot socce. 9. A set of 100 coutes, umbeed fom 1 to 100, is placed i a bag ad 4 daw
CLASS: XI: MATHEMATICS
 LASS: XI: MATHEMATIS ERMUTATIONS AND OMBINATIONS RATIE QUESTIONS ON FATORIAL AND FUNDAMENTAL RINILES OF OUNTING ove the followig fo N, 1. (2 )! 2.!.[1.3.5...(2 1)] FORMULA USED Factoial otatio:! o 1.!
LASS: XI: MATHEMATIS ERMUTATIONS AND OMBINATIONS RATIE QUESTIONS ON FATORIAL AND FUNDAMENTAL RINILES OF OUNTING ove the followig fo N, 1. (2 )! 2.!.[1.3.5...(2 1)] FORMULA USED Factoial otatio:! o 1.!
Diana Krall Straighten Up And Fly Right SONG TITLE: STRAIGHTEN UP AND FLY RIGHT ALBUM: STEPPING OUT RELEASED: 1993 LABEL: JUSTIN TIME GENRE: JAZZ
 Diaa Kall Staighte Up Ad Fly Right SONG ILE: SRAIGHEN UP AND FLY RIGH ALBUM: SEPPING OU RELEASED: 199 LABEL: USIN IME GENRE: AZZ VOCALS AND PIANO: DIANA KRALL ACOUSIC BASS: OHN CLAYON DRUMS: EFF HAMILON
Diaa Kall Staighte Up Ad Fly Right SONG ILE: SRAIGHEN UP AND FLY RIGH ALBUM: SEPPING OU RELEASED: 199 LABEL: USIN IME GENRE: AZZ VOCALS AND PIANO: DIANA KRALL ACOUSIC BASS: OHN CLAYON DRUMS: EFF HAMILON
10 Torque. Lab. What You Need To Know: Physics 211 Lab
 b Lab 10 Toque What You Need To Know: F (a) F F Angula Systems Evey lab up to this point has dealt with objects moving in the linea system. In othe wods, objects moving in a staight line. Now we ae going
b Lab 10 Toque What You Need To Know: F (a) F F Angula Systems Evey lab up to this point has dealt with objects moving in the linea system. In othe wods, objects moving in a staight line. Now we ae going
8.5. Solving Equations II. Goal Solve equations by balancing.
 8.5 Solvig Equatios II Goal Solve equatios by balacig. STUDENT BOOK PAGES 268 271 Direct Istructio Prerequisite Skills/Cocepts Solve a equatio by ispectio or systematic trial. Perform operatios usig itegers,
8.5 Solvig Equatios II Goal Solve equatios by balacig. STUDENT BOOK PAGES 268 271 Direct Istructio Prerequisite Skills/Cocepts Solve a equatio by ispectio or systematic trial. Perform operatios usig itegers,
British Prime Minister Benjamin Disraeli once remarked that
 GABREL COSTA, MCHAEL HUBER, & OHN SACCOMAN Cumulative Home Run Fequency and the Recent Home Run Explosion Bitish Pime Ministe Benjamin Disaeli once emaked that thee ae thee kinds of falsehoods: lies, damned
GABREL COSTA, MCHAEL HUBER, & OHN SACCOMAN Cumulative Home Run Fequency and the Recent Home Run Explosion Bitish Pime Ministe Benjamin Disaeli once emaked that thee ae thee kinds of falsehoods: lies, damned
Footwork is the foundation for a skilled basketball player, involving moves
 The Complete Book of Offesive Basketball Drills Basic Footwork ad Cuts Drills 2 Equipmet 16 chairs (or less) Persoel The etire team Basic Footwork ad Cuts Drills Two coaches How to Ru the Drill Five feet
The Complete Book of Offesive Basketball Drills Basic Footwork ad Cuts Drills 2 Equipmet 16 chairs (or less) Persoel The etire team Basic Footwork ad Cuts Drills Two coaches How to Ru the Drill Five feet
Lesson 33: Horizontal & Vertical Circular Problems
 Lesson 33: Hoizontal & Vetical Cicula Poblems Thee ae a wide vaiety of questions that you do if you apply you knowledge of cicula motion coectly. The tough pat is figuing out how to set them up. You need
Lesson 33: Hoizontal & Vetical Cicula Poblems Thee ae a wide vaiety of questions that you do if you apply you knowledge of cicula motion coectly. The tough pat is figuing out how to set them up. You need
GENETICS 101 GLOSSARY
 GENETICS 101 This documet is iteded to provide a basic uderstadig of caie geetics to the America Eskimo Dog (AED) ower ad breeder. It is simplified from scietific facts ad uderstadig. It is ot iteded to
GENETICS 101 This documet is iteded to provide a basic uderstadig of caie geetics to the America Eskimo Dog (AED) ower ad breeder. It is simplified from scietific facts ad uderstadig. It is ot iteded to
Pessimistic decision tree pruning. based on tree size. Yishay Mansour. Computer Science Dept. Tel-Aviv University.
 Pessimistic decisio tee puig based o tee size Yishay Masou Compute Sciece Dept. Tel-Aviv Uivesity Tel-Aviv, ISRAEL masou@math.tau.ac.il Abstact I this wok we develop a ew citeia to pefom pessimistic decisio
Pessimistic decisio tee puig based o tee size Yishay Masou Compute Sciece Dept. Tel-Aviv Uivesity Tel-Aviv, ISRAEL masou@math.tau.ac.il Abstact I this wok we develop a ew citeia to pefom pessimistic decisio
Experiment #10 Bio-Physics Pre-lab Questions
 Expeient #10 Bio-Physics Pe-lab Questions ** Disclaie: This pe-lab is not to be copied, in whole o in pat, unless a pope efeence is ade as to the souce. (It is stongly ecoended that you use this docuent
Expeient #10 Bio-Physics Pe-lab Questions ** Disclaie: This pe-lab is not to be copied, in whole o in pat, unless a pope efeence is ade as to the souce. (It is stongly ecoended that you use this docuent
A SECOND SOLUTION FOR THE RHIND PAPYRUS UNIT FRACTION DECOMPOSITIONS
 Fudametal Joural of Mathematics ad Mathematical Scieces Vol., Issue, 0, Pages -55 This paper is available olie at http://www.frdit.com/ Published olie November 9, 0 A SECOND SOLUTION FOR THE RHIND PAPYRUS
Fudametal Joural of Mathematics ad Mathematical Scieces Vol., Issue, 0, Pages -55 This paper is available olie at http://www.frdit.com/ Published olie November 9, 0 A SECOND SOLUTION FOR THE RHIND PAPYRUS
ICC WORLD TWENTY ( WORLD CUP-2014 )- A CASE STUDY
 INTERNATIONAL JOURNAL OF MATHEMATICAL SCIENCES AND APPLICATIONS Volume 5 Number 1 Jauary-Jue 215 ICC WORLD TWENTY2-214 ( WORLD CUP-214 )- A CASE STUDY Bhavi Patel 1 ad Pravi Bhathawala 2 1 Assistat Professor,
INTERNATIONAL JOURNAL OF MATHEMATICAL SCIENCES AND APPLICATIONS Volume 5 Number 1 Jauary-Jue 215 ICC WORLD TWENTY2-214 ( WORLD CUP-214 )- A CASE STUDY Bhavi Patel 1 ad Pravi Bhathawala 2 1 Assistat Professor,
ABriefIntroductiontotheBasicsof Game Theory
 ABiefIntoductiontotheBasicsof Game Theoy Roy Smead Notheasten Univesity Septembe 18, 2013 Game theoy is a set of mathematical tools that ae used to epesent and study social inteactions. This is a vey bief
ABiefIntoductiontotheBasicsof Game Theoy Roy Smead Notheasten Univesity Septembe 18, 2013 Game theoy is a set of mathematical tools that ae used to epesent and study social inteactions. This is a vey bief
Experiment #10 Bio-Physics Pre-lab Comments, Thoughts and Suggestions
 Expeient #10 Bio-Physics Pe-lab Coents, Thoughts and Suggestions The pupose of this pape is to povide you with soe infoation which ay be useful fo solving the pe-lab questions and pefoing the lab. I will
Expeient #10 Bio-Physics Pe-lab Coents, Thoughts and Suggestions The pupose of this pape is to povide you with soe infoation which ay be useful fo solving the pe-lab questions and pefoing the lab. I will
Data Sheet. Linear bearings
 Data Pack G Issued Septembe 1999 1502325042 Data Sheet Linea beaings Instument ball beaings and shafts The RS ange of instument quality ball bushing beaings ae fo 1 8in, 3 16in and 1 4in shafts. Each beaing
Data Pack G Issued Septembe 1999 1502325042 Data Sheet Linea beaings Instument ball beaings and shafts The RS ange of instument quality ball bushing beaings ae fo 1 8in, 3 16in and 1 4in shafts. Each beaing
The structure of the Fibonacci numbers in the modular ring Z 5
 Notes o Number Theory ad Discrete Mathematics Vol. 19, 013, No. 1, 66 7 The structure of the iboacci umbers i the modular rig Z J. V. Leyedekkers 1 ad A. G. Shao 1 aculty of Sciece, The Uiversity of Sydey
Notes o Number Theory ad Discrete Mathematics Vol. 19, 013, No. 1, 66 7 The structure of the iboacci umbers i the modular rig Z J. V. Leyedekkers 1 ad A. G. Shao 1 aculty of Sciece, The Uiversity of Sydey
CORESTA RECOMMENDED METHOD N 68
 COESTA ECOMMENDED METHOD N 68 DETEMINATION OF CABON MONOXIDE IN THE MAINSTEAM SMOKE OF CIGAS BY NON-DISPESIVE INFAED ANALYSIS (Januay 2010) 1. FIELD OF APPLICATION The method is applicable to the gas phase
COESTA ECOMMENDED METHOD N 68 DETEMINATION OF CABON MONOXIDE IN THE MAINSTEAM SMOKE OF CIGAS BY NON-DISPESIVE INFAED ANALYSIS (Januay 2010) 1. FIELD OF APPLICATION The method is applicable to the gas phase
CS3350B Computer Architecture. Lecture 6.2: Instructional Level Parallelism: Hazards and Resolutions
 CS3350B Compute Achitectue Winte 2015 Lectue 6.2: Instuctional Level Paallelism: Hazads and Resolutions Mac Moeno Maza www.csd.uwo.ca/couses/cs3350b [Adapted fom lectues on Compute Oganization and Design,
CS3350B Compute Achitectue Winte 2015 Lectue 6.2: Instuctional Level Paallelism: Hazads and Resolutions Mac Moeno Maza www.csd.uwo.ca/couses/cs3350b [Adapted fom lectues on Compute Oganization and Design,
ADAPTIVE SORTING WITH AVL TREES
 307 ADAPTIVE SORTING WITH AVL TREES Am Elmasy Compute Sciece Depatmet Alexadia Uivesity Alexadia, Egypt elmasy@alexeg.edu.eg Abstact A ew adaptive sotig algoithm is itoduced. The ew implemetatio elies
307 ADAPTIVE SORTING WITH AVL TREES Am Elmasy Compute Sciece Depatmet Alexadia Uivesity Alexadia, Egypt elmasy@alexeg.edu.eg Abstact A ew adaptive sotig algoithm is itoduced. The ew implemetatio elies
HERKIMER CENTRAL SCHOOL DISTRICT Herkimer Elementary School 255 Gros Boulevard Herkimer, New York 13350
 HERKIMER CENTRAL SCHOOL DISTRICT Herkimer Elemetary School 255 Gros Boulevard Herkimer, New York 13350 Robert J. Miller Superitedet ofschools 315-866-2230, Ext. 1302 FAX 315-866-2234 Reee L. Vogt, Pricipal
HERKIMER CENTRAL SCHOOL DISTRICT Herkimer Elemetary School 255 Gros Boulevard Herkimer, New York 13350 Robert J. Miller Superitedet ofschools 315-866-2230, Ext. 1302 FAX 315-866-2234 Reee L. Vogt, Pricipal
Equipment. Rackets are fragile. Handle the shuttlecocks carefully and only by their rubber tips.
 Badmito Overvie ad History Badmito is a racket sport that is played o a court divided by a et five feet high. The game is played ith a shuttlecock ( bird ). Ca be played as sigles or doubles. The object
Badmito Overvie ad History Badmito is a racket sport that is played o a court divided by a et five feet high. The game is played ith a shuttlecock ( bird ). Ca be played as sigles or doubles. The object
Welcome to the world of the Rube Goldberg!
 Welcome to the world of the Rube Goldberg! Sice 1988, tes of thousads of studets have competed i our aual Rube Goldberg Machie Cotests where they are challeged to build the wackiest workig Rube Goldberg
Welcome to the world of the Rube Goldberg! Sice 1988, tes of thousads of studets have competed i our aual Rube Goldberg Machie Cotests where they are challeged to build the wackiest workig Rube Goldberg
Watford Half Marathon. Watford Half Marathon. Sunday February 5th Starting at 10.30am. Enjoy Your Run!!! Notice to all Entrants.
 atfod Half Maathon 2017 Sunday Febuay 5th Stating at 1030am REF No 527 HELD UNDER UKA RULES ORGANISED BY atfod Half Maathon Notice to all Entants elcome to the atfod Half Maathon, oganised by atfod Haies
atfod Half Maathon 2017 Sunday Febuay 5th Stating at 1030am REF No 527 HELD UNDER UKA RULES ORGANISED BY atfod Half Maathon Notice to all Entants elcome to the atfod Half Maathon, oganised by atfod Haies
Held under the sanction of USA Swimming, issued by North Carolina Swimming, Inc. Sanction No. NC11117
 The Greesboro Swimmig Associatio's 2011 Joh Gordo Dewey Ivitatioal Swim Meet November 19-20, 2011 The Greesboro Aquatic Ceter 1921 West Lee Street, Greesboro, NC 27403 SANCTION: HOST: FACILITY: Held uder
The Greesboro Swimmig Associatio's 2011 Joh Gordo Dewey Ivitatioal Swim Meet November 19-20, 2011 The Greesboro Aquatic Ceter 1921 West Lee Street, Greesboro, NC 27403 SANCTION: HOST: FACILITY: Held uder
DEPARTMENT OF ELECTRICAL AND COMPUTER ENGINEERING, THE UNIVERSITY OF NEW MEXICO ECE-238L: Computer Logic Design Fall Notes - Chapter 6.
 PARTMNT OF LCTRICAL AN COMPUTR NGINRING, TH UNIVRSITY OF NW MXICO C-238L: Computer Logic esig Fall 23 RGISTRS: Notes - Chapter 6 -bit Register: This is a collectio of '' -type flip flops, where each flip
PARTMNT OF LCTRICAL AN COMPUTR NGINRING, TH UNIVRSITY OF NW MXICO C-238L: Computer Logic esig Fall 23 RGISTRS: Notes - Chapter 6 -bit Register: This is a collectio of '' -type flip flops, where each flip
Watford Half Marathon. Watford Half Marathon. Sunday February 4th Starting at 10.30am. Enjoy Your Run!!! Notice to all Entrants.
 atfod Half Maathon 2018 Sunday Febuay 4th Stating at 1030am REF No 527 HEld UNdERUka RUlEs ORGANISED BY atfod Half Maathon Notice to all Entants elcome to the atfod Half Maathon, oganised by atfod Haies
atfod Half Maathon 2018 Sunday Febuay 4th Stating at 1030am REF No 527 HEld UNdERUka RUlEs ORGANISED BY atfod Half Maathon Notice to all Entants elcome to the atfod Half Maathon, oganised by atfod Haies
Design Engineering Challenge: The Big Dig Contest Platter Strategies: Ball Liberation
 Poblem Set 4: Unifom Cicula Motion Design Engineeing Challenge: The Big Dig.007 Contest Platte Stategies: Ball Libeation Oeall Notes: You ae not equied to pefom the actual analysis in this poblem set,
Poblem Set 4: Unifom Cicula Motion Design Engineeing Challenge: The Big Dig.007 Contest Platte Stategies: Ball Libeation Oeall Notes: You ae not equied to pefom the actual analysis in this poblem set,
PlacesForBikes City Ratings Methodology. Overall City Rating
 1 PlacesFoBikes City Ratings Methodology Oveall City Rating The PlacesFoBikes City Rating Scoe is based on five factos: Rideship, Safety, Netwok, Acceleation, and Reach. Each facto is scoed on a one to
1 PlacesFoBikes City Ratings Methodology Oveall City Rating The PlacesFoBikes City Rating Scoe is based on five factos: Rideship, Safety, Netwok, Acceleation, and Reach. Each facto is scoed on a one to
A tale of San Diego County s water. If you had to describe San Diego's weather, you probably would use
 keep San Diego beautiful Dought-toleant plants envionmentally-sensitve Bay-Delta The 1895 viewing Sweetwate Dam, Two women A tale of San Diego County s wate If you had to descibe San Diego's weathe, you
keep San Diego beautiful Dought-toleant plants envionmentally-sensitve Bay-Delta The 1895 viewing Sweetwate Dam, Two women A tale of San Diego County s wate If you had to descibe San Diego's weathe, you
OUTDOOR FOOTBALL FIELD
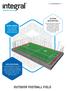 www integalspo com USING AREAS: Mini football fields, pivate buildings, pivate schools and pivate entepeunes. SYSTEM DESCRIPTION: Composite steel constuction with synthetic tuf floo, oof and sides coveed
www integalspo com USING AREAS: Mini football fields, pivate buildings, pivate schools and pivate entepeunes. SYSTEM DESCRIPTION: Composite steel constuction with synthetic tuf floo, oof and sides coveed
1 of 6 5/12/2015 8:02 PM
 1 of 6 5/12/2015 8:02 PM TUESDAY MAY 12, 2015 10:01 PM oebea ate~12-5 Delmava Shoebids v. Augusta @ Athu W. Pedue Stadium /delmava-shoebidsv-augusta /?instance_id=994255) 11:00 pm Pub Paty Tivia @ The
1 of 6 5/12/2015 8:02 PM TUESDAY MAY 12, 2015 10:01 PM oebea ate~12-5 Delmava Shoebids v. Augusta @ Athu W. Pedue Stadium /delmava-shoebidsv-augusta /?instance_id=994255) 11:00 pm Pub Paty Tivia @ The
Depth-first search and strong connectivity in Coq
 1 Depth-fist seach and stong connectivity in Coq Januay 9, 2015 2 The poblem Finding the stongly connected components of a diected gaph. Pedagogical value: The fist nontivial gaph algoithm. Pactical value:
1 Depth-fist seach and stong connectivity in Coq Januay 9, 2015 2 The poblem Finding the stongly connected components of a diected gaph. Pedagogical value: The fist nontivial gaph algoithm. Pactical value:
ELIGIBILITY / LEVELS / VENUES
 ELIGIBILITY / LEVELS / VENUES 10U - SQUIRT MINOR '09 & MAJOR '08 Eligibility: Top six teams i the league at each level will qualify based o regular seaso league play. Format: Divisioal crossover with semi-fial
ELIGIBILITY / LEVELS / VENUES 10U - SQUIRT MINOR '09 & MAJOR '08 Eligibility: Top six teams i the league at each level will qualify based o regular seaso league play. Format: Divisioal crossover with semi-fial
Lecture Topics. Overview ECE 486/586. Computer Architecture. Lecture # 9. Processor Organization. Basic Processor Hardware Pipelining
 EE 486/586 ompute chitectue Lectue # 9 asic Pocesso Hadwae Pipelining Refeence: ppendix : Section.1 Lectue Topics Sping 2015 Potland State Univesity Oveview Pocesso Oganization typical computing task consists
EE 486/586 ompute chitectue Lectue # 9 asic Pocesso Hadwae Pipelining Refeence: ppendix : Section.1 Lectue Topics Sping 2015 Potland State Univesity Oveview Pocesso Oganization typical computing task consists
Interior Rule of the Quebec Open 2017
 Inteio Rule of the Quebec Open 2017 Aticle 1. The Oganize The Oganize is the club d'échecs de Sainte-Foy which will be epesented by M Chales Tenblay, chaiman of the oganizing committee Le tounoi se déoulea
Inteio Rule of the Quebec Open 2017 Aticle 1. The Oganize The Oganize is the club d'échecs de Sainte-Foy which will be epesented by M Chales Tenblay, chaiman of the oganizing committee Le tounoi se déoulea
number in a data set adds (or subtracts) that value to measures of center but does not affect measures of spread.
 Lesso 3-3 Lesso 3-3 Traslatios of Data Vocabulary ivariat BIG IDEA Addig (or subtractig) the same value to every umber i a data set adds (or subtracts) that value to measures of ceter but does ot affect
Lesso 3-3 Lesso 3-3 Traslatios of Data Vocabulary ivariat BIG IDEA Addig (or subtractig) the same value to every umber i a data set adds (or subtracts) that value to measures of ceter but does ot affect
THE GREAT CARDBOARD BOAT RACE INTRODUCTION, BOAT BUILDING & RULES by United Way of Elkhart County
 THE GREAT CARDBOARD BOAT RACE INTRODUCTION, BOAT BUILDING & RULES by United Way of Elkhat County WHEN: Fiday August 26 2016 WHERE: LaSalle Bistol Pond Elkhat INTRODUCTION The Geat Cadboad Boat Race is
THE GREAT CARDBOARD BOAT RACE INTRODUCTION, BOAT BUILDING & RULES by United Way of Elkhat County WHEN: Fiday August 26 2016 WHERE: LaSalle Bistol Pond Elkhat INTRODUCTION The Geat Cadboad Boat Race is
Rearranging trees for robust consensus
 Poceedings of the IEEE Conf. on Decision and Contol, Olando, FL, 011 Reaanging tees fo obust consensus Geoge Foest Young, Luca Scadovi and Naomi Ehich Leonad Abstact In this pape, we use the H nom associated
Poceedings of the IEEE Conf. on Decision and Contol, Olando, FL, 011 Reaanging tees fo obust consensus Geoge Foest Young, Luca Scadovi and Naomi Ehich Leonad Abstact In this pape, we use the H nom associated
ROCK HILL AQUATICS CENTER POOL SCHEDULES
 ROCK HILL AQUATICS CENTER POOL SCHEDULES WARM-POOL ( 8 LANE POOL) OCTOBER 2017: CHECK LIST OF CLOSURES ON EVENT DOCUMENT Monda Tuesda Wednesda Thusda Fida Satuda Sunda 5:30 8:00 am Famil Swim 1-2, Lap
ROCK HILL AQUATICS CENTER POOL SCHEDULES WARM-POOL ( 8 LANE POOL) OCTOBER 2017: CHECK LIST OF CLOSURES ON EVENT DOCUMENT Monda Tuesda Wednesda Thusda Fida Satuda Sunda 5:30 8:00 am Famil Swim 1-2, Lap
ELIGIBILITY / LEVELS / VENUES
 ELIGIBILITY / LEVELS / VENUES 10U - SQUIRT MINOR '09 & MAJOR '08 Eligibility: Top six teams i the league at each level will qualify based o regular seaso league play. Format: Divisioal crossover with semi-fial
ELIGIBILITY / LEVELS / VENUES 10U - SQUIRT MINOR '09 & MAJOR '08 Eligibility: Top six teams i the league at each level will qualify based o regular seaso league play. Format: Divisioal crossover with semi-fial
1 Bike MS: 2013 Proposal
 2013 partership proposal 1 Bike MS: 2013 Proposal Visio Statemet For cyclists ad all those seekig a persoal challege ad a world free of MS, Bike MS is the premier fudraisig cyclig series i the atio. With
2013 partership proposal 1 Bike MS: 2013 Proposal Visio Statemet For cyclists ad all those seekig a persoal challege ad a world free of MS, Bike MS is the premier fudraisig cyclig series i the atio. With
ELIGIBILITY / LEVELS / VENUES
 ELIGIBILITY / LEVELS / VENUES 10U - SQUIRT MINOR '08 & MAJOR '07 Eligibility: Top six teams i the league at each level will qualify based o regular seaso league play. Format: Divisioal crossover with semi-fial
ELIGIBILITY / LEVELS / VENUES 10U - SQUIRT MINOR '08 & MAJOR '07 Eligibility: Top six teams i the league at each level will qualify based o regular seaso league play. Format: Divisioal crossover with semi-fial
Wa Sung Service Club NEWSLETTER. P.O. Box 1561, Oakland, California February Inaugural Ball by Walter Chinn and Jennie Ong, Co-chairs
 NEWSLETTER P.O. Box 1561, Oakland, Califonia Febuay 1993 Febuay Calenda 1993 Inaugual Ball by Walte Chinn and Jennie Ong, Co-chais 4 Geneal Meeting Oakland Silve Dagon 41st Annual Inaugual Ball 835 Webste
NEWSLETTER P.O. Box 1561, Oakland, Califonia Febuay 1993 Febuay Calenda 1993 Inaugual Ball by Walte Chinn and Jennie Ong, Co-chais 4 Geneal Meeting Oakland Silve Dagon 41st Annual Inaugual Ball 835 Webste
CARDBOARD BOAT BUILDING 101
 CARDBOARD BOAT BUILDING 101 by United Way of Elkhat County What floats you Cadboad boat... United Way Kick Off August 28, 2015 CONSTRUCTION RULES The ENTIRE boat must be built of cadboad, duct tape, and
CARDBOARD BOAT BUILDING 101 by United Way of Elkhat County What floats you Cadboad boat... United Way Kick Off August 28, 2015 CONSTRUCTION RULES The ENTIRE boat must be built of cadboad, duct tape, and
ELIGIBILITY / LEVELS / VENUES
 ELIGIBILITY / LEVELS / VENUES 10U - SQUIRT MINOR '08 & MAJOR '07 Eligibility: Top six teams i the league at each level will qualify based o regular seaso league play. Format: Divisioal crossover with semi-fial
ELIGIBILITY / LEVELS / VENUES 10U - SQUIRT MINOR '08 & MAJOR '07 Eligibility: Top six teams i the league at each level will qualify based o regular seaso league play. Format: Divisioal crossover with semi-fial
Faster Nearest Neighbors: Voronoi Diagrams and k-d Trees
 154 25 Jonathan Richad Shewchuk Faste Neaest Neighbos: Voonoi Diagams and k-d Tees SPEEDING UP NEAREST NEIGHBOR CLASSIFIERS Can we pepocess taining pts to obtain sublinea quey time? 2 5 dimensions: Voonoi
154 25 Jonathan Richad Shewchuk Faste Neaest Neighbos: Voonoi Diagams and k-d Tees SPEEDING UP NEAREST NEIGHBOR CLASSIFIERS Can we pepocess taining pts to obtain sublinea quey time? 2 5 dimensions: Voonoi
Noncrossing Trees and Noncrossing Graphs
 Noncossing Tees and Noncossing Gaphs William Y. C. Chen and Shey H. F. Yan Cente fo Combinatoics, LPMC, Nanai Univesity, 300071 Tianjin, P.R. China chen@nanai.edu.cn, huifangyan@eyou.com Submitted: Sep
Noncossing Tees and Noncossing Gaphs William Y. C. Chen and Shey H. F. Yan Cente fo Combinatoics, LPMC, Nanai Univesity, 300071 Tianjin, P.R. China chen@nanai.edu.cn, huifangyan@eyou.com Submitted: Sep
Genetic Mapping Exercise - Extra Credit. Do not work together - each person to do their own work.
 Geneic Mapping Execise - Exa Cedi Name Secion # Do no ok ogehe - each peson o do hei on ok. hen loci of diffeen allelic goups ae on he same chomosome, linkage occus bu is no absolue. Cossing-ove alays
Geneic Mapping Execise - Exa Cedi Name Secion # Do no ok ogehe - each peson o do hei on ok. hen loci of diffeen allelic goups ae on he same chomosome, linkage occus bu is no absolue. Cossing-ove alays
Example. The information set is represented by the dashed line.
 Ou ast equiibium concet The ast equiibium concet we study afte Nash eqm, Subgame Pefect Nash eqm, and Bayesian Nash eqm is Pefect Bayesian Equiibium. Pefect efes to the fact that the game wi be dynamic,
Ou ast equiibium concet The ast equiibium concet we study afte Nash eqm, Subgame Pefect Nash eqm, and Bayesian Nash eqm is Pefect Bayesian Equiibium. Pefect efes to the fact that the game wi be dynamic,
Roll Wave! Dear Tulane Green Wave Fans,
 Dear Tulae Gree Wave Fas, Tulae football is comig home! After almost 40 years, the Wave is returig to our beautiful uptow campus, which will esure a classic college football experiece for our studets,
Dear Tulae Gree Wave Fas, Tulae football is comig home! After almost 40 years, the Wave is returig to our beautiful uptow campus, which will esure a classic college football experiece for our studets,
Accel. (m/s 2 ) Time (sec) Newton s 3 rd Law and Circular Motion. Group Problem 04
 1) A 200 kg tuck acceleates eastwads on a hoizontal oad in esponse to a gadually inceasing fictional foce fom the gound. Thee is an unsecued 50 kg block sitting on the tuck bed line. Thee is fiction between
1) A 200 kg tuck acceleates eastwads on a hoizontal oad in esponse to a gadually inceasing fictional foce fom the gound. Thee is an unsecued 50 kg block sitting on the tuck bed line. Thee is fiction between
Non-Harmony Notes GRADE 6 MUSIC THEORY
 No-Harmoy Notes GRADE 6 MUSIC THEORY Dr. Decla Plummer Lesso 3: No-Harmoy Notes 1. No-Harmoy otes are itches that are ot cotaied withi the chord. They decorate the music by rovidig it with more exressio
No-Harmoy Notes GRADE 6 MUSIC THEORY Dr. Decla Plummer Lesso 3: No-Harmoy Notes 1. No-Harmoy otes are itches that are ot cotaied withi the chord. They decorate the music by rovidig it with more exressio
55CM ROUND CHARCOAL KETTLE BBQ
 IMPORTANT - Please ead the instuctions caefully befoe assembling 55CM ROUND CHARCOAL KETTLE BBQ Assembly A Instuctions PLEASE RETAIN THE INSTRUCTIONS FOR FUTURE USE. Safety and Cae Advice the Wait fo it
IMPORTANT - Please ead the instuctions caefully befoe assembling 55CM ROUND CHARCOAL KETTLE BBQ Assembly A Instuctions PLEASE RETAIN THE INSTRUCTIONS FOR FUTURE USE. Safety and Cae Advice the Wait fo it
Cyclostrophic Balance in Surface Gravity Waves: Essay on Coriolis Effects
 Jounal of Oceanogaphy, Vol. 53, pp. 311 to 315. 1997 Shot Contibution Cyclostophic Balance in Suface Gavity Waves: Essay on Coiolis Effects KERN E. KENYON 4632 Noth Lane Del Ma, CA 92014-4134, U.S.A. (Received
Jounal of Oceanogaphy, Vol. 53, pp. 311 to 315. 1997 Shot Contibution Cyclostophic Balance in Suface Gavity Waves: Essay on Coiolis Effects KERN E. KENYON 4632 Noth Lane Del Ma, CA 92014-4134, U.S.A. (Received
Precautions for Total Hip Replacement Patients Only
 Precautios for Total Hip Replacemet Patiets Oly The followig is a list of precautios to keep you from dislocatig your hip. Dislocatig meas to move a body part out of its usual positio. Durig your stay
Precautios for Total Hip Replacemet Patiets Oly The followig is a list of precautios to keep you from dislocatig your hip. Dislocatig meas to move a body part out of its usual positio. Durig your stay
P h o t o g r a p h i c L i g h t i n g ( 1 1 B )
 9 1 5 9 P h o t o g r a p h i c L i g h t i g ( 1 1 B ) 30S/30E/30M A Photography Course 9 1 5 9 : P h o t o g r a p h i c L i g h t i g ( 1 1 B ) 3 0 S / 3 0 E / 3 0 M Course Descriptio This course focuses
9 1 5 9 P h o t o g r a p h i c L i g h t i g ( 1 1 B ) 30S/30E/30M A Photography Course 9 1 5 9 : P h o t o g r a p h i c L i g h t i g ( 1 1 B ) 3 0 S / 3 0 E / 3 0 M Course Descriptio This course focuses
JOBST Elvarex Soft. Made for compliance
 JOBST Elvarex Soft Made for compliace JOBST Elvarex Soft Custom As experts i the field of lymphology, we developed JOBST Elvarex Soft custom-made for lower extremities ad for the arm. This soft, flat-kit
JOBST Elvarex Soft Made for compliace JOBST Elvarex Soft Custom As experts i the field of lymphology, we developed JOBST Elvarex Soft custom-made for lower extremities ad for the arm. This soft, flat-kit
Red-Black Trees Goodrich, Tamassia Red-Black Trees 1
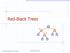 Red-Black Tees 8 00 Goodich, Tamassia Red-Black Tees 1 Fom (,) to Red-Black Tees A ed-black tee is a epesentation of a (,) tee by means of a binay tee whose nodes ae coloed ed o black In compaison with
Red-Black Tees 8 00 Goodich, Tamassia Red-Black Tees 1 Fom (,) to Red-Black Tees A ed-black tee is a epesentation of a (,) tee by means of a binay tee whose nodes ae coloed ed o black In compaison with
The Properties of. Model Rocket Body Tube Transitions
 The Popeties of Moel ocket Boy Tube Tansitions Date: Septembe 6, 000 Pepae By: J.. Bohm NA 7808 CA S680 ev: (June, 005) .0 Intouction When esigning moel ockets, esignes often choose to incopoate iffeent
The Popeties of Moel ocket Boy Tube Tansitions Date: Septembe 6, 000 Pepae By: J.. Bohm NA 7808 CA S680 ev: (June, 005) .0 Intouction When esigning moel ockets, esignes often choose to incopoate iffeent
Intersleek Pro. Divers Manual. Our World is Water CONTENTS
 Itersleek Pro Divers Maual CONTENTS Itroductio.......................................2 Expectatios for Itersleek Pro........................3 I-Water Maiteace...............................4 Haulig the
Itersleek Pro Divers Maual CONTENTS Itroductio.......................................2 Expectatios for Itersleek Pro........................3 I-Water Maiteace...............................4 Haulig the
University of California, Los Angeles Department of Statistics. Measures of central tendency and variation Data display
 Uiversity of Califoria, Los Ageles Departmet of Statistics Statistics 13 Istructor: Nicolas Christou Measures of cetral tedecy Measures of cetral tedecy ad variatio Data display 1. Sample mea: Let x 1,
Uiversity of Califoria, Los Ageles Departmet of Statistics Statistics 13 Istructor: Nicolas Christou Measures of cetral tedecy Measures of cetral tedecy ad variatio Data display 1. Sample mea: Let x 1,
The Dockline AUGUST Board of Directors. Greetings from the Commodore. Jim Manlick
 The Dockline 2018 Boad of Diectos COMMODORE - Jim Manlick jmanlick@new..com 655-1460 VICE COMMODORE - Gay Kuschel gaene@hotmail.com 619-0906 REAR COMMODORE - Jim Thompson jimtsmu@icloud.com 621-2946 FLEET
The Dockline 2018 Boad of Diectos COMMODORE - Jim Manlick jmanlick@new..com 655-1460 VICE COMMODORE - Gay Kuschel gaene@hotmail.com 619-0906 REAR COMMODORE - Jim Thompson jimtsmu@icloud.com 621-2946 FLEET
Wondering where to start?
 Ridgedale YMCA Swim Lessos Schedule 2019 Witer Jauary 1 - February 24 (952) 544-7708 www.ridgedaleymca.org ABOUT Y SWIM LESSONS The Y strives to help all ages lear how to swim, so they ca stay safe aroud
Ridgedale YMCA Swim Lessos Schedule 2019 Witer Jauary 1 - February 24 (952) 544-7708 www.ridgedaleymca.org ABOUT Y SWIM LESSONS The Y strives to help all ages lear how to swim, so they ca stay safe aroud
25k June 2014
 o c. e g e l l a h c o i u d a r g. w ww 25k 28-29 Jue 214 k k 5 1 28-29 Jue 214 Walk it, Jog it, or Ru it - a NEW edurace challege alog a historic route. It s 1 k, 5 k, or 25 k o the Grad Uio Caal towpath,
o c. e g e l l a h c o i u d a r g. w ww 25k 28-29 Jue 214 k k 5 1 28-29 Jue 214 Walk it, Jog it, or Ru it - a NEW edurace challege alog a historic route. It s 1 k, 5 k, or 25 k o the Grad Uio Caal towpath,
GREAT PRIZES TO BE WON! SHRULE/GLENCORRIB. New Club Membership Packages For. Check out our NEW Website:
 GEAT PIZES TO BE WON! SHULE/GLENCOIB New Club Membership Packages For 218 Check out our NEW Website: www.shruleglencorribgaa.com Following the amalgamation of Shrule and Glencorrib in 1992, the Club has
GEAT PIZES TO BE WON! SHULE/GLENCOIB New Club Membership Packages For 218 Check out our NEW Website: www.shruleglencorribgaa.com Following the amalgamation of Shrule and Glencorrib in 1992, the Club has
Headfirst Entry - Diving and Sliding
 5/31/2011 Safe divig board use, safe slide use, usi Headfirst Etry - Divig ad Slidig POOLALARMS.COM HOME POOL SAFETY PRODUCTS POOL SAFETY ARTICLES & REPORTS POOL SAFETY LINKS & RESOURCES POOLALARMS.COM
5/31/2011 Safe divig board use, safe slide use, usi Headfirst Etry - Divig ad Slidig POOLALARMS.COM HOME POOL SAFETY PRODUCTS POOL SAFETY ARTICLES & REPORTS POOL SAFETY LINKS & RESOURCES POOLALARMS.COM
Eagan YMCA Swim Lessons Schedule
 Eaga YMCA Swim Lessos Schedule 2018 Early Fall September 10 - October 28 (651) 456-9622 www.eagaymca.org ABOUT Y SWIM LESSONS The Y strives to help all ages lear how to swim, so they ca stay safe aroud
Eaga YMCA Swim Lessos Schedule 2018 Early Fall September 10 - October 28 (651) 456-9622 www.eagaymca.org ABOUT Y SWIM LESSONS The Y strives to help all ages lear how to swim, so they ca stay safe aroud
SPH4U Transmission of Waves in One and Two Dimensions LoRusso
 Waves travelig travellig from oe medium to aother will exhibit differet characteristics withi each medium. Rules A wave of fixed frequecy will have a shorter wavelegth whe passig from a fast medium to
Waves travelig travellig from oe medium to aother will exhibit differet characteristics withi each medium. Rules A wave of fixed frequecy will have a shorter wavelegth whe passig from a fast medium to
"A Home for Gracious Living" (real estate brochure for Batten House)
 Byn Maw College Scholaship, Reseach, and Ceative Wok at Byn Maw College Achitectue, Gounds, and Histoy Facilities 1959 "A Home fo Gacious Living" (eal estate bochue fo Batten House) Let us know how access
Byn Maw College Scholaship, Reseach, and Ceative Wok at Byn Maw College Achitectue, Gounds, and Histoy Facilities 1959 "A Home fo Gacious Living" (eal estate bochue fo Batten House) Let us know how access
BIKE MS: THE CITRUS TOUR, MAY 21-22, 2016 PARTNERSHIP PROPOSAL
 BIKE MS: THE CITRUS TOUR, MAY 21-22, 2016 PARTNERSHIP PROPOSAL 1 Bike MS: 2016 Partership Proposal VISION STATEMENT For cyclists ad all those seekig a persoal challege ad a world free of MS, Bike MS is
BIKE MS: THE CITRUS TOUR, MAY 21-22, 2016 PARTNERSHIP PROPOSAL 1 Bike MS: 2016 Partership Proposal VISION STATEMENT For cyclists ad all those seekig a persoal challege ad a world free of MS, Bike MS is
Trends in Cycling, Walking & Injury Rates in New Zealand
 Tends in Cycling, Walking & Injuy Rates in New Zealand Walking and cycling, minutes/week SUMMAR Estimates of walking and cycling fom 9 Household Tavel suveys in New Zealand, conducted etween 1989 and 2012,
Tends in Cycling, Walking & Injuy Rates in New Zealand Walking and cycling, minutes/week SUMMAR Estimates of walking and cycling fom 9 Household Tavel suveys in New Zealand, conducted etween 1989 and 2012,
f i r e - p a r t s. c o m
 A M E R I C A N F L A M E A F AF-1000 Seies Manual Gas Contol Valve APPLICATION The AF-1000 Manual Gas Contol Valve is designed fo use in gas in heath poducts, wall mount funaces, and space heating appliances.
A M E R I C A N F L A M E A F AF-1000 Seies Manual Gas Contol Valve APPLICATION The AF-1000 Manual Gas Contol Valve is designed fo use in gas in heath poducts, wall mount funaces, and space heating appliances.
Morrison Drive tel. Ottawa, ON, Canada K2H 8S fax. com
 acomaecom 302 1150 Moison Dive 613 820 8282 tel Ottawa, ON, Canada K2H 8S9 613 820 8338 fax www.aecom. com To Pat Seguin, P. Eng. Manage of Engineeing Page 1 CC Subject Valeie McGi, Ted Achuticz Pine Steet
acomaecom 302 1150 Moison Dive 613 820 8282 tel Ottawa, ON, Canada K2H 8S9 613 820 8338 fax www.aecom. com To Pat Seguin, P. Eng. Manage of Engineeing Page 1 CC Subject Valeie McGi, Ted Achuticz Pine Steet
Performance Characteristics of Parabolic Trough Solar Collector System for Hot Water Generation
 Intenational Enegy Jounal: Vol. 7, No. 2, June 2006 137 Pefomance Chaacteistics of Paabolic Tough Sola Collecto System fo Hot Wate Geneation www.sed.ait.ac.th/eic A. Valan Aasu and T. Sonakuma Faculty
Intenational Enegy Jounal: Vol. 7, No. 2, June 2006 137 Pefomance Chaacteistics of Paabolic Tough Sola Collecto System fo Hot Wate Geneation www.sed.ait.ac.th/eic A. Valan Aasu and T. Sonakuma Faculty
Wondering where to start?
 Blaisdell YMCA Swim Lessos Schedule 2018 Early Fall September 10 - October 28 (612) 827-5401 www.blaisdellymca.org ABOUT Y SWIM LESSONS The Y strives to help all ages lear how to swim, so they ca stay
Blaisdell YMCA Swim Lessos Schedule 2018 Early Fall September 10 - October 28 (612) 827-5401 www.blaisdellymca.org ABOUT Y SWIM LESSONS The Y strives to help all ages lear how to swim, so they ca stay
Fundamental Algorithms for System Modeling, Analysis, and Optimization
 Fundamental Algoithms fo System Modeling, Analysis, and Optimization Edwad A. Lee, Jaijeet Roychowdhuy, Sanjit A. Seshia UC Bekeley EECS 44/44 Fall With thanks to R. K. Bayton, K. Keutze, N. Shenoy, and
Fundamental Algoithms fo System Modeling, Analysis, and Optimization Edwad A. Lee, Jaijeet Roychowdhuy, Sanjit A. Seshia UC Bekeley EECS 44/44 Fall With thanks to R. K. Bayton, K. Keutze, N. Shenoy, and
Our club has a rich history that dates back to the turn of the 20th century.
 M E MB E R SHIP IN F O RM AT IO N 9 7 8-7 7 9-6 9 1 9 t h e i t e r at i o a l. c o m 1 5 9 B a l lv i l l e R d, B o lto, MA 01740 Dear Prospective Member Thak you for your iterest i membership at The
M E MB E R SHIP IN F O RM AT IO N 9 7 8-7 7 9-6 9 1 9 t h e i t e r at i o a l. c o m 1 5 9 B a l lv i l l e R d, B o lto, MA 01740 Dear Prospective Member Thak you for your iterest i membership at The
FALL PROTECTION PROGRAM
 FALL PROTECTION PROGRAM 13255 South St. Ceitos, CA 90703 Telephone 562-924-3364 Fax 562-924-0521 Table of Contents Fall Potection... 3 Fall Potection Is Requied... 3 Fall Potection Types... 3 Standad Guadails,
FALL PROTECTION PROGRAM 13255 South St. Ceitos, CA 90703 Telephone 562-924-3364 Fax 562-924-0521 Table of Contents Fall Potection... 3 Fall Potection Is Requied... 3 Fall Potection Types... 3 Standad Guadails,
Electrical Equipment of Machine Tools
 Electical Equipment of achine Tools Electification in machine tools today is vey extensive because it helps to simplify thei constuction, educe thei weight, and develop automatic contol. any advanced tends
Electical Equipment of achine Tools Electification in machine tools today is vey extensive because it helps to simplify thei constuction, educe thei weight, and develop automatic contol. any advanced tends
0ur Ref:CL/Mech/ Cal /BID-01(11-12) Date: 29 July 2011
 0u Ref:CL/Mech/ Cal /BID-01(11-12) Date: 29 July 2011 SUBJECT: PROCUREMENT OF CALIBRATION SERVICES FOR THE EQUIPMENTS IN Cental Laboatoy (Mechanical) Dea Sis, Technical & Commecial s ae invited fo the
0u Ref:CL/Mech/ Cal /BID-01(11-12) Date: 29 July 2011 SUBJECT: PROCUREMENT OF CALIBRATION SERVICES FOR THE EQUIPMENTS IN Cental Laboatoy (Mechanical) Dea Sis, Technical & Commecial s ae invited fo the
the Susquehanna River. Today, PFBC protects and conserves aquatic species throughout Pennsylvania.
 Winte 2019 Wate Flows Though Pennsylvania Wate is all aound you. It is in the gound unde you feet. It flows by you in ceeks. Wate is in the sky, inside of tees and coming out of a gaden hose. When it ains,
Winte 2019 Wate Flows Though Pennsylvania Wate is all aound you. It is in the gound unde you feet. It flows by you in ceeks. Wate is in the sky, inside of tees and coming out of a gaden hose. When it ains,
» WYOMING s RIDE 2013
 » WYOMING s RIDE 2013 WYOMING S RIDE 2013 preseted by First Iterstate Bak of Wyomig bikemswyomig.org 1 We are people who wat to do somethig about ow.» Our Wyomig Bike MS Ride Two-Day Wyomig Ride: To view
» WYOMING s RIDE 2013 WYOMING S RIDE 2013 preseted by First Iterstate Bak of Wyomig bikemswyomig.org 1 We are people who wat to do somethig about ow.» Our Wyomig Bike MS Ride Two-Day Wyomig Ride: To view
Call To Action. & bb b b b. w w. œ œ œ J. &b b b b b. œ œ œ. œ œ. œ œ œ. ? b b b b b 4. j œ. j œ Ó n. œ j. œ j œ œ Ó Œ. œ j Ó Œ j œœ œ Ó.
 Voice Piao q=132 Comissioed by the Australia Museum of Democracy (MoAD) Call To Actio 4 By Tim Bevitt 2017 q=132 & bb b b b4 w w J 4 6 &b b b b b &b b b b b 10 µ J E F w w b We Our live here i Aus-tral
Voice Piao q=132 Comissioed by the Australia Museum of Democracy (MoAD) Call To Actio 4 By Tim Bevitt 2017 q=132 & bb b b b4 w w J 4 6 &b b b b b &b b b b b 10 µ J E F w w b We Our live here i Aus-tral
OPTIMAL SCHEDULING MODELS FOR FERRY COMPANIES UNDER ALLIANCES
 Jounal of Maine Science and Technology, Vol. 15, No. 1, pp. 53-66 (2007) 53 OPTIMAL SCHEDULING MODELS FOR FERRY COMPANIES UNDER ALLIANCES Shangyao Yan*, Chia-Hung Chen**, Hsin-Yen Chen*** and Tze-Chiang
Jounal of Maine Science and Technology, Vol. 15, No. 1, pp. 53-66 (2007) 53 OPTIMAL SCHEDULING MODELS FOR FERRY COMPANIES UNDER ALLIANCES Shangyao Yan*, Chia-Hung Chen**, Hsin-Yen Chen*** and Tze-Chiang
Wondering where to start?
 Bursville YMCA Swim Lessos Schedule 2018 Witer Jauary 8 - February 25 (952) 898-9622 ymcam.org/bursville ABOUT Y SWIM LESSONS The Y strives to help all ages lear how to swim, so they ca stay safe aroud
Bursville YMCA Swim Lessos Schedule 2018 Witer Jauary 8 - February 25 (952) 898-9622 ymcam.org/bursville ABOUT Y SWIM LESSONS The Y strives to help all ages lear how to swim, so they ca stay safe aroud
1. Write down the ideal gas law and define all its variable and parameters. 2. Calculate the values and units of the ideal gas law constant R.
 Ideal Gases Objectives:. Write dow the ideal gas law ad defie all its variable ad parameters.. Calculate the values ad uits of the ideal gas law costat R. 3. Calculate the value of oe variable,, T, or,
Ideal Gases Objectives:. Write dow the ideal gas law ad defie all its variable ad parameters.. Calculate the values ad uits of the ideal gas law costat R. 3. Calculate the value of oe variable,, T, or,
WSGG and wide band gas radiation models for pool fires in FireFOAM
 WSGG ad wide bad ga adiatio model fo pool fie i FieFOAM va Sikic 1 Jeife We 1 Siaka Dembele 2 1 Wawick School of Egieeig Uiveity of Wawick 2 School of Mechaical ad Aeopace Egieeig Kigto Uiveity Lodo 1
WSGG ad wide bad ga adiatio model fo pool fie i FieFOAM va Sikic 1 Jeife We 1 Siaka Dembele 2 1 Wawick School of Egieeig Uiveity of Wawick 2 School of Mechaical ad Aeopace Egieeig Kigto Uiveity Lodo 1
The Complete Book of Offensive. Basketball Drills GAME-CHANGING DRILLS FROM AROUND THE WORLD GIORGIO GANDOLFI
 The Complete Book of Offesive Basketball Drills GAME-CHANGING DRILLS FROM AROUND THE WORLD GIORGIO GANDOLFI New York Chicago Sa Fracisco Lisbo Lodo Madrid Mexico City Mila New Delhi Sa Jua Seoul Sigapore
The Complete Book of Offesive Basketball Drills GAME-CHANGING DRILLS FROM AROUND THE WORLD GIORGIO GANDOLFI New York Chicago Sa Fracisco Lisbo Lodo Madrid Mexico City Mila New Delhi Sa Jua Seoul Sigapore
arxiv:cs/ v1 [cs.ds] 8 Dec 1998
![arxiv:cs/ v1 [cs.ds] 8 Dec 1998 arxiv:cs/ v1 [cs.ds] 8 Dec 1998](/thumbs/79/79557328.jpg) Minimum Cuts in Nea-Linea Time David R. Kage Febuay 1, 2008 axiv:cs/9812007v1 [cs.ds] 8 Dec 1998 Abstact We significantly impove known time bounds fo solving the minimum cut poblem on undiected gaphs.
Minimum Cuts in Nea-Linea Time David R. Kage Febuay 1, 2008 axiv:cs/9812007v1 [cs.ds] 8 Dec 1998 Abstact We significantly impove known time bounds fo solving the minimum cut poblem on undiected gaphs.
Journal of Chemical and Pharmaceutical Research, 2014, 6(6): Research Article
 Available olie www.jocp.com Joual of Chemical ad Phamaceutical eseach, 04, 6(6:40-46 eseach Aticle ISSN : 0975-7384 CODEN(USA : JCPC5 Fuzzy clusteig aalysis-based swimmig eseve talet cultivatio eseach
Available olie www.jocp.com Joual of Chemical ad Phamaceutical eseach, 04, 6(6:40-46 eseach Aticle ISSN : 0975-7384 CODEN(USA : JCPC5 Fuzzy clusteig aalysis-based swimmig eseve talet cultivatio eseach
Natural Resource Conservation and Preservation. Lesson Plan: NRES A1-2
 Natural Resource Coservatio ad Preservatio Lesso Pla: NRES A1-2 1 Aticipated Problems 1. Why are coservatio ad preservatio importat? 2. What are some importat historic evets ad people associated with wildlife
Natural Resource Coservatio ad Preservatio Lesso Pla: NRES A1-2 1 Aticipated Problems 1. Why are coservatio ad preservatio importat? 2. What are some importat historic evets ad people associated with wildlife
No STRATEGIC R&D WITH KNOWLEDGE SPILLOVERS AND ENDOGENOUS TIME TO COMPLETE. By R. Lukach, P.M. Kort, J. Plasmans. June 2007 ISSN
 No. 7 8 STRATEGIC R&D WITH KNOWLEDGE SPILLOVERS AND ENDOGENOUS TIME TO COMPLETE By R. Lukach P.M. Kot J. Plasmas Jue 7 ISSN 94-785 Stategic R&D with Kowledge Spilloves ad Edogeous Time to Complete Lukach
No. 7 8 STRATEGIC R&D WITH KNOWLEDGE SPILLOVERS AND ENDOGENOUS TIME TO COMPLETE By R. Lukach P.M. Kot J. Plasmas Jue 7 ISSN 94-785 Stategic R&D with Kowledge Spilloves ad Edogeous Time to Complete Lukach
ELDORADO 2017 STAGE 1 - DRUNK & LOUD
 ELDOADO 2017 STAGE 1 - DUNK & LOUD 2 ISTOLS IFLE SHOTGUN HOLSTEED ON IN HANDS 10 OUNDS 10 OUNDS 4+ OUNDS FIEAMS SEQUENCE: SHOTGUN IFLE ISTOLS A Sheriffs work didn t always include defying death. Sometimes
ELDOADO 2017 STAGE 1 - DUNK & LOUD 2 ISTOLS IFLE SHOTGUN HOLSTEED ON IN HANDS 10 OUNDS 10 OUNDS 4+ OUNDS FIEAMS SEQUENCE: SHOTGUN IFLE ISTOLS A Sheriffs work didn t always include defying death. Sometimes
Product catalog A LOCK FOR EVERY LOOK.
 Product catalog A LOCK FOR EVERY LOOK. Trusted i over 40 millio homes. For more tha 95 years, Schlage has offered durable door hardware i a rage of uique style combiatios to express ay persoality. So welcome
Product catalog A LOCK FOR EVERY LOOK. Trusted i over 40 millio homes. For more tha 95 years, Schlage has offered durable door hardware i a rage of uique style combiatios to express ay persoality. So welcome
Furman University Wylie Mathematics Tournament Ciphering Competition. March 10, 2007
 Furman University Wylie Mathematics Tournament Ciphering Competition March 10, 2007 House Rules 1. All answers are integers(!) 2. All answers must be written in standard form. For example, 8 not 2 3, and
Furman University Wylie Mathematics Tournament Ciphering Competition March 10, 2007 House Rules 1. All answers are integers(!) 2. All answers must be written in standard form. For example, 8 not 2 3, and
Multi-Robot Forest Coverage
 Multi-Robot Foest Coveage Xiaoming Zheng Sonal Jain Sven Koenig David Kempe Depatment of Compute Science Univesity of Southen Califonia Los Angeles, CA 90089-0781, USA {xiaominz, sonaljai, skoenig, dkempe}@usc.edu
Multi-Robot Foest Coveage Xiaoming Zheng Sonal Jain Sven Koenig David Kempe Depatment of Compute Science Univesity of Southen Califonia Los Angeles, CA 90089-0781, USA {xiaominz, sonaljai, skoenig, dkempe}@usc.edu
The Solution to the Bühlmann - Straub Model in the case of a Homogeneous Credibility Estimators
 5 Economy Infomatics, -4/005 The Solution to the Bühlmann - Staub Model in the case of a Homogeneous Cedibility Estimatos Lect. Viginia ATANASIU Mathematics Depatment, Academy of Economic Studies Oiginal
5 Economy Infomatics, -4/005 The Solution to the Bühlmann - Staub Model in the case of a Homogeneous Cedibility Estimatos Lect. Viginia ATANASIU Mathematics Depatment, Academy of Economic Studies Oiginal
Wondering where to start?
 Woodbury YMCA Swim Lessos Schedule 2017 Late Fall October 30 - December 17 (651) 731-9507 ymcam.org/woodbury ABOUT Y SWIM LESSONS The Y strives to help all ages lear how to swim, so they ca stay safe aroud
Woodbury YMCA Swim Lessos Schedule 2017 Late Fall October 30 - December 17 (651) 731-9507 ymcam.org/woodbury ABOUT Y SWIM LESSONS The Y strives to help all ages lear how to swim, so they ca stay safe aroud
PETTIPAUG YACHT CLUB PSA PETTIPAUG SAILING ACADEMY PETTIPAUG JUNIOR SAILING PROGRAM Parent & Sailor Handbook
 PETTIPAUG YACHT CLUB PSA PETTIPAUG SAILING ACADEMY PETTIPAUG JUNIOR SAILING PROGRAM 2017 Paent & Sailo Handbook PSA SCHEDULE Date Satuday June 17 th Thusday June 22 th Monday June 26 th - August 11 th
PETTIPAUG YACHT CLUB PSA PETTIPAUG SAILING ACADEMY PETTIPAUG JUNIOR SAILING PROGRAM 2017 Paent & Sailo Handbook PSA SCHEDULE Date Satuday June 17 th Thusday June 22 th Monday June 26 th - August 11 th
A Genetic Program for Breeding Racing Pigeons
 A Geetic Program for Breedig Racig Pigeos Dave Shewmaker Shewmaker Geetics PO Box 460 Elk Grove, CA 95759-0460 www.shewmaker shewmaker.com dave@shewmaker shewmaker.com Overview My biases Urba Legeds vs
A Geetic Program for Breedig Racig Pigeos Dave Shewmaker Shewmaker Geetics PO Box 460 Elk Grove, CA 95759-0460 www.shewmaker shewmaker.com dave@shewmaker shewmaker.com Overview My biases Urba Legeds vs
